Документация

Что такое вейвлет?

Вейвлет является формой волны эффективно ограниченной длительности, которая имеет среднее значение нуля и ненулевую норму.

Многие интересующие сигналы и изображения демонстрируют кусочно-плавное поведение, пунктуированное переходными процессами. Речевые сигналы характеризуются короткими пакетами, кодирующими согласные, за которыми следуют установившиеся колебания, указывающие на гласные. Натуральные изображения имеют ребра. Финансовые временные ряды демонстрируют переходное поведение, которое характеризует быстрый подъем и спад в экономических условиях. В отличие от базиса Фурье, вейвлеты основ имеют ограниченное представление кусочно-регулярных сигналов и изображений, которые включают переходное поведение.

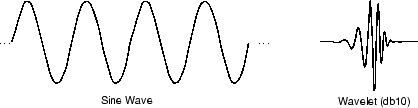
Сравните вейвлеты с синусоидами, которые являются базисом анализа Фурье. Синусоиды не имеют ограниченной длительности - они простираются от минус до плюс бесконечности. В то время как синусоиды являются гладкими и предсказуемыми, вейвлеты, как правило, являются нерегулярными и асимметричными.

Анализ Фурье состоит из разбиения сигнала на синусоиды различных частот. Аналогично, вейвлет-анализ является разбиением сигнала на сдвинутые и масштабированные версии исходного (или материнского) вейвлета.

Просто глядя на фотографии вейвлетов и синусоид, вы можете интуитивно увидеть, что сигналы с резкими изменениями могут быть лучше проанализированы нерегулярным вейвлетом, чем с гладкой синусоидой.

Также имеет смысл, что локальные признаки могут быть описаны лучше с вейвлетами, которые имеют локальную протяженность. Следующий пример иллюстрирует это для простого сигнала, состоящего из синусоиды с разрывом.

t = linspace(0,1,100)';
x = sin(2*pi*t);
x1 = x-0.15;
y = zeros(size(x));
y(1:length(y)/2) = x(1:length(y)/2);
y(length(y)/2+1:end) = x1(length(y)/2+1:end);
stem(t,y,'markerfacecolor',[0 0 1]); 
xlabel('Seconds'); 
ylabel('Amplitude');

[swa,swd] = swt(y,1,'sym2');
subplot(211)
stem(t,y,'markerfacecolor',[0 0 1]); 
title('Original Signal');
subplot(212)
stem(t,swd,'markerfacecolor',[0 0 1]);
title('Level 1 Wavelet Coefficients');

dftsig = fft([x y]);
dftsig = dftsig(1:length(y)/2+1,:);
df = 100/length(y);
freq = 0:df:50;
stem(freq,abs(dftsig));
xlabel('Hz'); ylabel('Magnitude');
legend('sine wave','sine wave with discontinuity');

[swax,swdx] = swt(x,1,'sym2');
subplot(211)
stem(t,swd); title('Sine Wave with Discontinuity (Wavelet Coefficients)');
subplot(212)
stem(t,swdx); title('Sine Wave (Wavelet Coefficients)');