В этом разделе рассматриваются функции оценки 1-D регрессии вейвлета с помощью одного из специализированных инструментов Wavelet Toolbox™. Тулбокс предоставляет приложение Wavelet Analyzer, чтобы исследовать некоторое шумоподавление для одинаково или неравномерно выбранных данных.
Для примеров в этом разделе переключите режим расширения на симметричное заполнение с помощью команды
dwtmode('sym')
Запустите инструмент 1-D оценки регрессии.
Из MATLAB® приглашение, тип waveletAnalyzer.
Появится Wavelet Analyzer.
Выберите меню Regression Estimation 1-D элемента. Появляется дискретный инструмент вейвлет для оценки 1-D регрессии.
Загрузка данных.
В командной строке MATLAB введите
load blocregdata;
В инструменте 1-D оценки регрессии выберите File > Import from Workspace. Когда появится диалоговое окно Импорт из рабочей области (Import from Workspace), выберите blocregdata данные. Нажмите кнопку ОК, чтобы импортировать данные. Отображаются загруженные и обработанные данные, полученные после раскладывания.
Выберите обработанные данные.
Значение по умолчанию для количества интервалов - 256 для этого примера. Введите 64 в поле редактирования интервалов Nb (количество интервалов) или используйте ползунок, чтобы настроить значение. Появятся новые привязанные данные, которые будут обработаны.
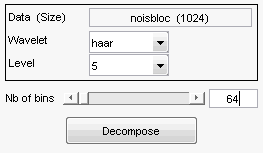
Привязанные данные, по-видимому, очень сглаживаются. Выберите 1000 из списка интервалов Nb и нажмите Enter или используйте ползунок. Появятся новые обрабатываемые данные.
Привязанные данные, по-видимому, очень близки к исходным данным, так как noisbloc имеет длину 1024.
Выполните Вейвлет Разложение обработанных данных.
Выберите haar вейвлет из меню Wavelet и выберите 5 из меню Level, а затем нажмите кнопку Descompose. После паузы для расчетов инструмент отображает коэффициенты детализации разложения.
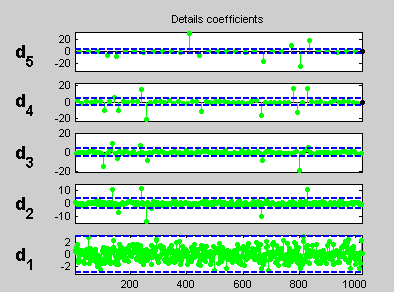
Выполните оценку регрессии.
В то время как для подстройки алгоритма оценки доступен ряд опций, мы примем значения по умолчанию мягкого порога фиксированной формы и немасштабированного белого шума. Ползунки, расположенные справа от окна, управляют зависимыми от уровня порогами, обозначенными желтыми пунктирными линиями, проходящими горизонтально через графики в левой части окна.
Продолжите, нажав кнопку Оценка.
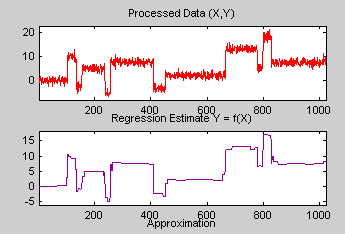
Видно, что процесс удалил шум и что блоки хорошо реконструированы. Оценка регрессии (в жёлтом цвете) является суммой расположенных ниже неё сигналов: приближение a5 и восстановленные детали после порога коэффициента.
Можно экспериментировать с различными предопределенными стратегиями порога, выбрав соответствующие опции в меню, расположенном в правой части окна, или непосредственно перетащив желтые горизонтальные линии левой кнопкой мыши.
Теперь давайте проиллюстрировать оценку регрессии, используя приложение Wavelet Analyzer для случайным или нерегулярно разнесенных наблюдений, фокусируясь на различиях от предыдущей ситуации.
В меню Файла выберите Данные Load > для Stochastic Проекта Regression опции. Когда появится диалоговое окно Загрузка данных для регрессии Стохастического проекта (Load data for Stochastic Design Regression), выберите MAT-файл ex1nsto.mat, который должен находиться в папке MATLAB toolbox/wavelet/wavelet. Нажмите кнопку OK. Этот короткий набор данных (размера 500) загружается в инструмент Regression Estimation 1-D -- Stochastic Design.
Отображаются загруженные данные, обозначенные (X, Y), гистограмма X и обработанные данные, полученные после раскладывания. Гистограмма интересна, потому что значения X распределены случайным образом. Шаг раскладывания необходим, поскольку он преобразует задачу оценки регрессии для нерегулярно разнесенных данных X в классическую схему фиксированного проекта, для которой могут использоваться быстрые вейвлеты преобразования.
Выберите sym4 вейвлет из меню «Вейвлет», выберите 5 из меню «Уровень» и введите 125 в поле редактирования интервалов Nb. Нажмите кнопку «Разложить». Инструмент отображает коэффициенты детализации разложения.
В меню Select thresholding method выберите элемент Penalize low и нажмите кнопку Estimate.
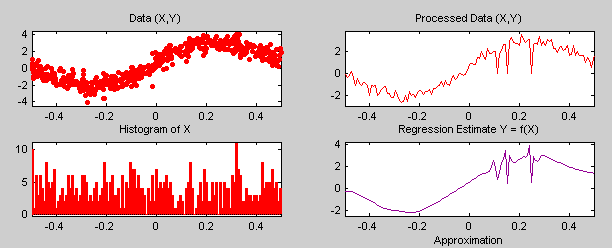
Проверьте Overlay Estimated Function, чтобы подтвердить подгонку исходных данных.
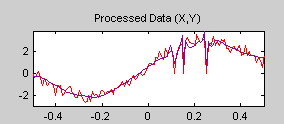
Этот инструмент позволяет вам сохранить предполагаемую функцию на диск. Тулбокс создает MAT-файл в текущей папке с выбранным именем.
Чтобы сохранить предполагаемую функцию из текущей оценки, используйте опцию меню File > Save Estimated Function. Появляется диалоговое окно, которое позволяет вам задать папку и имя файла для хранения функции. Введите имя fex1nsto. После сохранения данных функции в файл fex1nsto.mat, загрузите переменные в рабочую область:
load fex1nsto whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
thrParams | 1x5 | 580 | cell array |
wname | 1x4 | 8 | char array |
xdata | 1x125 | 1000 | double array |
ydata | 1x125 | 1000 | double array |
Предполагаемая функция определяется xdata и ydata. Длина этих векторов равна количеству интервалов, которые вы выбираете на шаге 2. В сложение параметры процесса оценки задаются именем вейвлета, содержащимся в wname:
wname
wname =
sym4
и зависящие от уровня пороги, содержащиеся в thrParams, который является массивом ячеек длиной 5 (уровень разложения). Для i от 1 до 5, thrParams{i} содержит нижнюю и верхнюю границы интервала порога и пороговое значение (поскольку допускаются интервально зависимые пороги). Для получения дополнительной информации смотрите 1-D «Адаптивное пороговое значение коэффициентов вейвлет» в Руководстве пользователя Wavelet Toolbox.
Для примера, для уровня 1,
thrParams{1}
ans =
-0.4987 0.4997 1.0395
Чтобы загрузить данные для оценки регрессии, ваши данные должны быть в форме массива структур с точно двумя полями. Поля должны быть именованы xdata и ydata, и должна быть одинаковой длины.
Например, загрузите файл, содержащий данные, рассмотренные в предыдущем примере:
clear load ex1nsto whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
xdata | 1x500 | 4000 | double array |
ydata | 1x500 | 4000 | double array |
В конце этого раздела поверните режим расширения назад к нулевому заполнению с помощью команды
dwtmode('zpd')