Этот раздел демонстрирует функции многомасштабного анализа основных компонентов, представленных в программном обеспечении Wavelet Toolbox™. Тулбокс включает в себя wmspca функция и Wavelet Analyzer приложение. В этом разделе описываются методы командной строки и приложения, а также информация о передаче информации о сигнале и параметре между диском и приложением.
Цель многомасштабного PCA состоит в том, чтобы восстановить, начиная с многомерного сигнала и используя простое представление на каждом уровне разрешения, упрощенный многомерный сигнал. Многомасштабные основные компоненты обобщают нормальную PCA многомерного сигнала, представленного в виде матрицы, путем выполнения PCA на матрицах деталей различных уровней одновременно. PCA также выполняется на матрице более грубых коэффициентов приближения в вейвлет области а также на конечной восстановленной матрице. Путем выбора количества сохраненных главных компонентов могут быть восстановлены интересные упрощенные сигналы.
Поскольку вы можете выполнить многомасштабный PCA либо из командной строки, либо с помощью приложения, в этом разделе есть подразделы, охватывающие каждый метод.
Этот пример использует шумные тестовые сигналы. В этом разделе вы будете:
Загрузка многомерного сигнала.
Выполните простой многомасштабный PCA.
Отображение исходных и упрощенных сигналов.
Улучшите полученный результат, удерживая меньше основных компонентов.
Загрузите многомерный сигнал путем ввода в MATLAB® приглашение:
load ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
covar | 4x4 | 128 | double array |
x | 1024x4 | 32768 | double array |
x_orig | 1024x4 | 32768 | double array |
Данные, сохраненные в матричных x происходит от двух тестовых сигналов, Blocks и HeavySine, и от их суммы и различия, к которой был добавлен многомерный белый шум Гауссова.
Выполните простой многомасштабный PCA.
Multiscale PCA объединяет noncentered PCA на аппроксимациях и деталях в вейвлете области и окончательном PCA. На каждом уровне выбираются наиболее важные основные компоненты.
Сначала установите параметры вейвлета:
level= 5; wname = 'sym4';
Затем автоматически выберите количество сохраненных основных компонентов, используя правило Кайзера путем набора
npc = 'kais';
Наконец, выполните многомасштабный PCA:
[x_sim, qual, npc] = wmspca(x ,level, wname, npc);
Отобразите оригинальные и упрощенные сигналы:
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x (:,i)); set(gca,'xtick',[]);
axis tight;
title(['Original signal ',num2str(i)])
subplot(4,2,kp+2), plot(x_sim(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Simplified signal ',num2str(i)])
kp = kp + 2;
end
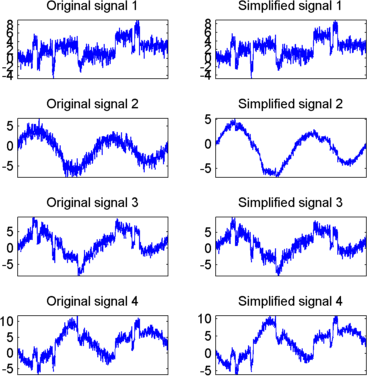
Результаты с точки зрения сжатия хороши. Проценты, отражающие качество восстановления столбца, заданные относительными средними квадратными ошибками, близки к 100%.
qual qual = 98.0545 93.2807 97.1172 98.8603
Улучшите первый результат, сохранив меньше основных компонентов.
Результаты могут быть улучшены путем подавления шума, потому что детали на уровнях 1-3 состоят по существу из шума с небольшими вкладами от сигнала. Удаление шума приводит к грубому, но большому, обесценивающему эффекту.
Выходной аргумент npc содержит номера сохраненных основных компонентов, выбранных правилом Кайзера:
npc
npc =
1 1 1 1 1 2 2
Для d от 1 до 5, npc(d) количество сохраненных нецентрированных основных компонентов (ПК) для получения дополнительной информации на уровне d. Количество сохраненных нецентрированных ПК для приближений на уровне 5 npc(6), и npc(7) количество сохраненных ПК для окончательного PCA после вейвлета реконструкции. Как ожидалось, правило сохраняет два основных компонента, как для приближений PCA, так и для окончательного PCA, но один основной компонент сохраняется для получения подробной информации на каждом уровне.
Чтобы подавить детали на уровнях с 1 по 3, обновите npc аргумент следующего содержания:
npc(1:3) = zeros(1,3); npc npc = 0 0 0 1 1 2 2
Затем снова выполните многомасштабный PCA:
[x_sim, qual, npc] = wmspca(x, level, wname, npc);
Отображение исходных и конечных упрощенных сигналов:
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x (:,i)); set(gca,'xtick',[]);
axis tight;
title(['Original signal ',num2str(i)]); set(gca,'xtick',[]);
axis tight;
subplot(4,2,kp+2), plot(x_sim(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Simplified signal ',num2str(i)])
kp = kp + 2;
end
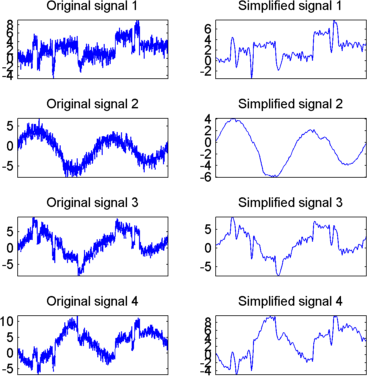
Как показано, результаты улучшены.
В этом разделе рассматриваются многомасштабные PCA с помощью приложения Wavelet Analyzer.
Откройте приложение Wavelet Analyzer путем набора waveletAnalyzer в командной строке.
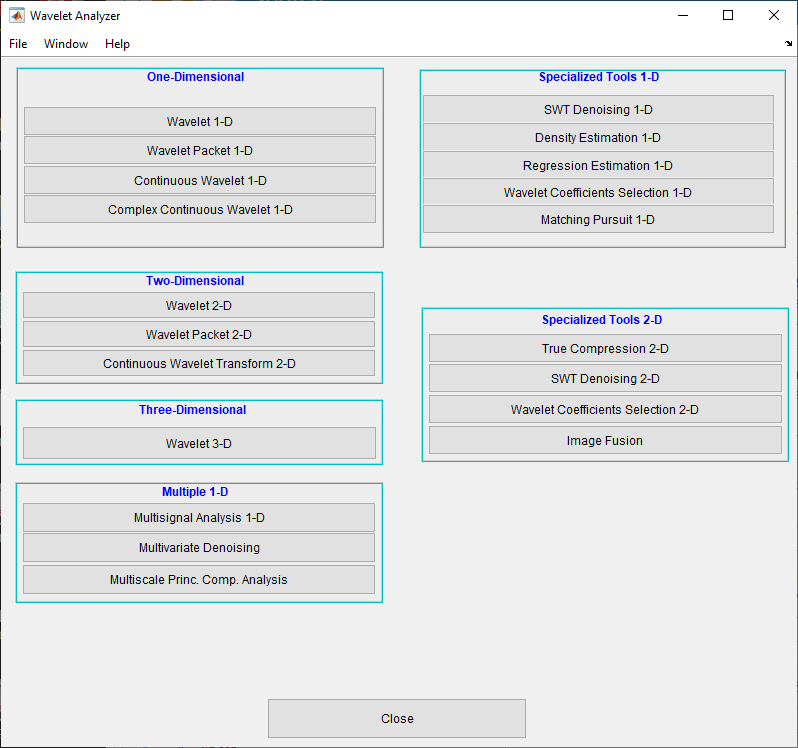
Нажмите Multiscale Princ. Comp. Analysis, чтобы открыть инструмент Multiscale Principal Components Analysis в приложении.
Загрузка данных.
В командной строке MATLAB введите
load ex4mwden
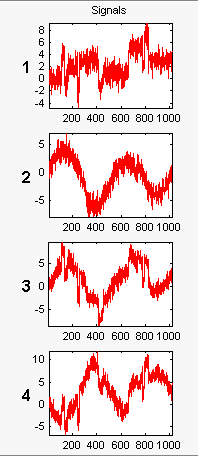
Эти сигналы являются шумными версиями из простых комбинаций двух исходных сигналов, Blocks и HeavySine и их суммы и различия, каждый с добавлением многомерного Гауссова белого шума.
Выполните вейвлет и диагонализируйте каждую матрицу коэффициентов.
Используйте значения по умолчанию для вейвлет, DWT Extension Mode и Descomposion Level, а затем нажмите Descompose and Diagonalize. Инструмент отображает вейвлет приближения и коэффициенты детализации разложения каждого сигнала в исходном базисе.
Чтобы получить дополнительные сведения о новых основах, разрешенных для выполнения PCA для каждой шкалы, нажмите кнопку Дополнительно на адаптированном базисе. Новый рисунок отображает соответствующие собственные векторы и собственные значения для матрицы коэффициентов детализации на уровне 1.

Можно изменить уровень или выбрать более грубые приближения или восстановленную матрицу, чтобы исследовать различные основы. Когда вы закончите, нажмите кнопку Закрыть.
Выполните простой многомасштабный PCA.
Начальные значения для PCA приводят к сохранению всех компонентов. Выберите Kaiser в раскрывающемся списке Предоставить по умолчанию и нажмите Применить.
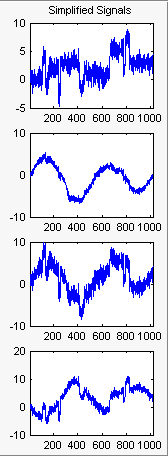
Результаты хороши с точки зрения сжатия.
Улучшите полученный результат путем сохранения меньшего количества основных компонентов.
Результаты могут быть улучшены путем подавления шума, потому что детали на уровнях 1-3 состоят по существу из шума с небольшими вкладами от сигнала, что можно увидеть при тщательном осмотре коэффициентов детализации. Удаление шума приводит к грубому, но большому, обесценивающему эффекту.
Для D1, D2 и D3 выберите 0 как Nb. нецентрированного ПК и нажмите Применить.
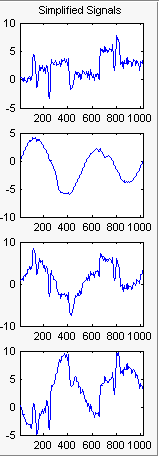
Результаты лучше, чем ранее полученные. Первый сигнал, который является нерегулярным, все еще правильно восстановлен, в то время как второй сигнал, который является более регулярным, деноидируется лучше после этого второго каскада PCA. Для получения дополнительной информации щелкните Невязки.
Инструмент Multiscale Principal Components Analysis позволяет сохранять упрощенные сигналы на диск. Тулбокс создает MAT-файл в текущей папке с именем по вашему выбору.
Для сохранения упрощенных сигналов из предыдущего раздела:
Выберите «Файл» > «Сохранить упрощенные сигналы».
Выберите «Сохранить упрощенные сигналы и параметры». Появляется диалоговое окно, которое позволяет вам задать папку и имя файла для хранения сигнала.
Введите имя s_ex4mwden и нажмите OK, чтобы сохранить данные.
Загрузите переменные в рабочую область:
load s_ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
PCA_Params | 1x7 | 2628 | struct array |
x | 1024x4 | 32768 | double array |
Упрощенные сигналы указаны в матрице x. Параметры multiscale PCA доступны в PCA_Params:
PCA_Params
PCA_Params =
1x7 struct array with fields:
pc
variances
npc
PCA_Params - массив структур длиной d+2 (здесь максимальный уровень разложения d=5) таким образом, что PCA_Params(d).pc - матрица основных компонентов. Столбцы хранятся в порядке убывания отклонений. PCA_Params(d).variances является вектором отклонений основного компонента и PCA_Params(d).npc - вектор выбранных чисел сохраненных главных компонентов.