Документация

Проводной решатель

Следующее является сокращенным описанием деривации уравнений, решенных для проводным решателем. Для более подробной информации см. [1].

Для PEC (Совершенный электрически проведение) провода, граничные условия требуют, чтобы тангенциальный компонент общего электрического поля на проводной поверхности был нулем:

Можно также описать уравнение в терминах поверхностной плотности тока, $${\overrightarrow{J}}_s$$, на проводе PEC и его пространственной производной. Это сделано путем интеграции эффекта поверхностной плотности тока с помощью функции Грина, $$g(\left|\overrightarrow{r}-{\overrightarrow{r}}^{\text{'}}\right|)$$. Функция Грина абстрактно представляет эффект бесконечно малого источника поверхностной плотности тока, расположенного в $${\overrightarrow{r}}^{\text{'}}$$ на электрических и магнитных полях в наблюдательном посте $$\overrightarrow{r}$$. Функция Грина для распространения свободного пространства:

где $$k=\omega \sqrt{{\epsilon }_0{\mu }_0}$$ номер волны, и ω является угловой частотой. В общем случае следующие шаги необходимы, чтобы решить электромагнитное (EM) проблема и получить поля EM в носителе. Чтобы представлять проблему EM точно, и продольные и поперечные составляющие интегрированного тока учтены на проводной поверхности и требуют того Eq. (1) держит над целой проводной поверхностью. Дискретизируйте Eq. (1) по конечному множеству точек или основных функций, чтобы получить набор уравнений. Дискретизируйте поверхностную плотность тока в конечное множество основных функций, чтобы получить набор неизвестных. Решите систему уравнений неизвестных, чтобы дать к дискретному приближению поверхностной текущей плотности на проводе. Эти плотности тока включают вычисление электромагнитных полей в любой желаемой точке. Для тонких проводов перечисленные выше шаги являются исчерпывающими и, упрощают функцию Грина до:

также называемый тонко-проводным приближением ядра, где $$r_a=\sqrt{r^2+a^2}$$ аппроксимированное среднее значение расстояния $$\left|\overrightarrow{r}-{\overrightarrow{r}}^{\text{'}}\right|$$, r является расстоянием между бесконечно малым поверхностным источником плотности тока и проводной осью, и a является проводным радиусом. Кроме того, плотность тока на проводе заменяется проводным током $$I=2\pi a\left|{\overrightarrow{J}}_s\right|$$|. Используя вышеупомянутое приближение, запишите Eq. (1) как:

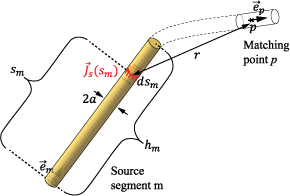
где s является продольным местоположением вдоль провода и $$\overrightarrow{e}(s)$$ единичный вектор, представляющий проводную ориентацию в том местоположении. Дискретизируйте провод в конечное число сегментов s(m) где m = 1....N, и затем далее дискретизируйте Eq. (4) в конечное множество уравнений, наложенных в точках, совпадающих с p = 1....N получить:

где _Im(sm) является распределением тока вдоль сегмента m, аппроксимированного полиномом формы:

с _hm, являющимся длиной сегмента и _nm выбранная степень полинома (который отличается от сегмента до сегмента). Замена Eq. (6) в (5), система уравнений может быть написана в матричном формате как:

где [_Zp,mi] является матрицей импеданса, [_Imi] вектор из неизвестных коэффициентов, представляющих ток на проводе, и [_Vexp,p] вектор возбуждения. Больше подробной информации о вычислении элементов [_Zp,mi] предоставлено в [1].