Основанный на крутящем моменте, ориентированный на поле контроллер для постоянного магнита поверхностного монтажа синхронный двигатель
Powertrain Blockset / Движение / Электродвигатели и Инверторы
Motor Control Blockset / Электрические системы / Двигатели
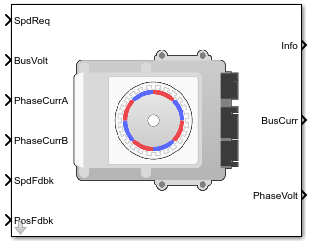
Блок Surface Mount PM Controller реализует основанный на крутящем моменте, ориентированный на поле контроллер для постоянного магнита синхронного двигателя (PMSM) поверхностного монтажа с дополнительным контроллером скорости внешнего контура. Управление крутящим моментом использует текущую квадратуру и не ослабляет магнитный поток. Можно задать или скорость или закрутить управление.
Surface Mount PM Controller реализует уравнения для регулировки скорости, определения крутящего момента, регуляторов, преобразований координат и двигателей.
Фигура иллюстрирует информационный поток в блоке.
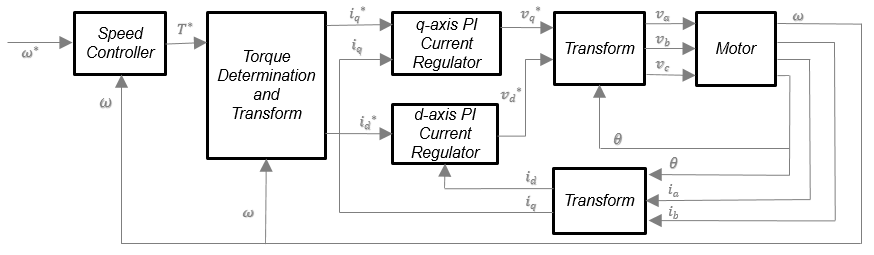
Блок реализует уравнения, которые используют эти переменные.
| ω | Скорость ротора |
| ω* | Команда скорости ротора |
| T* | Закрутите команду |
id i*d | текущая d-ось d-ось текущая команда |
iq i*q | текущая q-ось q-ось текущая команда |
vd, v*d | напряжение d-оси команда напряжения d-оси |
vq v*q | напряжение q-оси команда напряжения q-оси |
| va, vb, vc | Фаза a Stator, b, c напряжения |
| ia, ib, ic | Фаза a Stator, b, c токи |
Чтобы реализовать контроллер скорости, выберите параметр Control Type Speed Control. Если вы выбираете параметр Control Type Torque Control, блок не реализует контроллер скорости.
Контроллер скорости определяет команду крутящего момента путем реализования фильтра состояния и вычисления команд обратной связи и feedforward. Если вы не реализуете контроллер скорости, введите команду крутящего момента с блоком Surface Mount PM Controller.
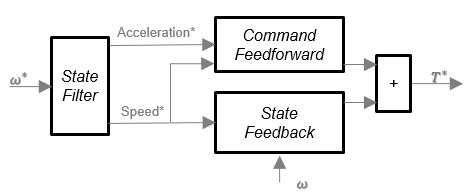
Фильтр состояния является фильтром lowpass, который генерирует ускоряющую команду на основе команды скорости. На вкладке Speed Controller:
Чтобы сделать время задержки команды скорости незначительным, задайте параметр Bandwidth of the state filter.
Чтобы вычислить усиление Speed regulation time constant, Ksf на основе полосы пропускания фильтра состояния, выберите Calculate Speed Regulator Gains.
Дискретной формой характеристического уравнения дают:
Фильтр вычисляет усиление с помощью этого уравнения.
Уравнения используют эти переменные.
| EVsf | Полоса пропускания фильтра команды скорости |
| Tsm | Контроллер движения шаг расчета |
| Ksf | Постоянная времени регулятора скорости |
Чтобы сгенерировать крутящий момент обратной связи состояния, блок использует отфильтрованный сигнал скоростной погрешности от фильтра состояния. Вычисление крутящего момента обратной связи также требует усилений для регулятора скорости.
На вкладке Speed Controller выберите Calculate Speed Regulator Gains, чтобы вычислить:
Proportional gain, ba
Angular gain, Ksa
Rotational gain, Kisa
Для вычислений усиления блок использует инерцию от значения параметров Physical inertia, viscous damping, static friction на вкладке Motor Parameters.
Усиления для обратной связи состояния вычисляются с помощью этих уравнений.
| Вычисление | Уравнения |
|---|---|
| Дискретные формы характеристического уравнения | |
Пропорциональная составляющая регулятора скорости | |
Интегральная составляющая регулятора скорости | |
Усиление двойного интеграла регулятора скорости |
Уравнения используют эти переменные.
| P | Моторные пары полюса |
| ba | Пропорциональная составляющая регулятора скорости |
| Ksa | Интегральная составляющая регулятора скорости |
| Kisa | Усиление двойного интеграла регулятора скорости |
| Jp | Инерция двигателя |
| Tsm | Контроллер движения шаг расчета |
Чтобы сгенерировать крутящий момент прямого распространения состояния, блок использует отфильтрованную скорость и ускорение от фильтра состояния. Кроме того, вычисление крутящего момента прямого распространения использует инерцию, вязкое затухание и статическое трение. Чтобы достигнуть нулевой ошибки отслеживания, команда крутящего момента является суммой feedforward и команд крутящего момента обратной связи.
Выбор Calculate Speed Regulator Gains на вкладке Speed Controller обновляет инерцию, вязкое затухание и статическое трение со значениями параметров Physical inertia, viscous damping, static friction на вкладке the Motor Parameters.
Команда крутящего момента прямого распространения использует это уравнение.
Уравнение использует эти переменные.
| Jp | Инерция двигателя |
| Tcmd_ff | Команда крутящего момента feedforward |
| Fs | Статический постоянный момент трения |
| Fv | Вязкий постоянный момент трения |
| Fs | Статический постоянный момент трения |
| ωm | Скорость ротора |
Блок использует квадратуру, текущую, чтобы определить номинальную скорость и текущие команды. Доступное напряжение на шине определяет номинальную скорость. Прямое (d) и квадратура (q) постоянный магнит (PM), определяет вызванное напряжение.
| Вычисление | Уравнения |
|---|---|
| Моторный максимальный крутящий момент | |
| Максимальная текущая фаза q-оси | |
| Электрическая номинальная скорость | |
| напряжение d-оси | |
| напряжение q-оси | |
| Максимальная текущая фаза | |
| Максимальное напряжение | |
| Текущая команда | Если Еще Если Еще Конец Конец |
Уравнения используют эти переменные.
| imax | Максимальная текущая фаза |
| id | текущая d-ось |
| iq | текущая q-ось |
| idref | текущая ссылка d-оси |
| iqref | текущая ссылка q-оси |
| iq_max | Максимальная текущая фаза q-оси |
| ωe | Ротор электрическая скорость |
| λpm | Потокосцепление постоянного магнита |
| vd | напряжение d-оси |
| vq | напряжение q-оси |
| vmax | Максимальная линия к нейтральному напряжению |
| vbus | Напряжение на шине DC |
| Ld | d-ось извилистая индуктивность |
| Lq | q-ось извилистая индуктивность |
| P | Моторные пары полюса |
| Tmax | Моторный максимальный крутящий момент |
| Tcmd | Моторный максимальный крутящий момент, которым управляют, |
Блок регулирует ток с антизаключительной функцией. Классический пропорциональный интегратор (PI) текущие регуляторы не рассматривает d-ось и связь q-оси или электромагнитную спиной силу (EMF) связь. В результате эффективность переходного процесса ухудшается. С учетом связи блок реализует комплексный вектор текущий регулятор (CVCR) в скалярном формате системы координат ротора. CVCR разъединяется:
d-ось и q-ось текущая перекрестная связь
перекрестная связь коэффициента противо-ЭДС
Ответ частоты тока является системой первого порядка с полосой пропускания EVcurrent.
Блок реализует эти уравнения.
| Вычисление | Уравнения |
|---|---|
| Моторное напряжение, в системе координат ротора | |
| Текущие усиления регулятора | |
| Передаточные функции |
Уравнения используют эти переменные.
| EVcurrent | Текущая полоса пропускания регулятора |
| id | текущая d-ось |
| iq | текущая q-ось |
| Kp_d | Текущее усиление d-оси регулятора |
| Kp_q | Текущее усиление q-оси регулятора |
| Ki | Текущее усиление интегратора регулятора |
| Ld | d-ось извилистая индуктивность |
| Lq | q-ось извилистая индуктивность |
| Rs | Сопротивление обмотки фазы Stator |
| ωm | Скорость ротора |
| vd | напряжение d-оси |
| vq | напряжение q-оси |
| λpm | Потокосцепление постоянного магнита |
| P | Моторные пары полюса |
Чтобы вычислить напряжения и токи в трехфазном сбалансированном (a, b) количества, двухфазная квадратура (α, β) количества, и вращающийся (d, q) системы координат, блок использует Преобразования Кларка и Парка.
В уравнениях преобразования.
| Преобразовать | Описание | Уравнения |
|---|---|---|
Кларк | Преобразует сбалансированные трехфазные количества (a, b) в сбалансированные двухфазные квадратурные количества (α, β). | |
Парк | Преобразует сбалансированные двухфазные ортогональные стационарные количества (α, β) в ортогональную систему координат вращения (d, q). | |
Инверсия Кларк | Преобразует сбалансированные двухфазные квадратурные количества (α, β) в сбалансированные трехфазные количества (a, b). | |
Обратный парк | Преобразует ортогональную систему координат вращения (d, q) в сбалансированные двухфазные ортогональные стационарные количества (α, β). |
Преобразования используют эти переменные.
| ωm | Скорость ротора |
| P | Моторные пары полюса |
| ωe | Ротор электрическая скорость |
| Θe | Ротор электрический угол |
| x | Ток фазы или напряжение |
Блок использует токи фазы и напряжения фазы, чтобы оценить текущую шину DC. Положительный ток указывает на выброс батареи. Отрицательный ток указывает на заряд батареи. Блок использует эти уравнения.
|
Загрузите степень | |
|
Исходная степень | |
|
Текущая шина DC | |
|
Предполагаемый крутящий момент ротора | |
|
Потери мощности для одного источника КПД, чтобы загрузить | |
|
Потери мощности для одного КПД загружают к источнику | |
|
Потери мощности для сведенного в таблицу КПД |
Уравнения используют эти переменные.
| va, vb, vc |
Фаза a Stator, b, c напряжения |
| vbus |
Предполагаемое напряжение на шине DC |
| ia, ib, ic |
Фаза a Stator, b, c токи |
| ibus |
Предполагаемая текущая шина DC |
| Eff |
Полный КПД инвертора |
| ωm |
Скорость механического устройства ротора |
| Lq |
q-ось извилистая индуктивность |
| Ld |
d-ось извилистая индуктивность |
| iq |
текущая q-ось |
| id |
текущая d-ось |
| λ |
Потокосцепление постоянного магнита |
| P |
Моторные пары полюса |
Задавать электрические потери, на вкладке Electrical Losses, для Parameterize losses by, избранной одной из этих опций.
| Установка | Блокируйте реализацию |
|---|---|
Single efficiency measurement | Электрическая потеря вычислила использование постоянного значения для КПД инвертора. |
Tabulated loss data | Электрическая потеря вычисляется в зависимости от частот вращения двигателя и крутящих моментов нагрузки. |
Tabulated efficiency data | Электрическая потеря вычислила с помощью КПД инвертора, который является функцией частот вращения двигателя и крутящих моментов нагрузки.
|
Для лучшей практики используйте Tabulated loss data вместо Tabulated efficiency data:
КПД заболевает заданный для нулевой скорости или нулевого крутящего момента.
Можно объяснить постоянные составляющие потерь, которые все еще присутствуют для нулевой скорости или крутящего момента.
[1] Лоренц, Роберт Д., Томас Липо и Дональд В. Новотни. “Движение управляет с асинхронными двигателями”. Продолжения IEEE®, Издание 82, Выпуск 8, август 1994, стр 1215–1240.
[2] Shigeo Morimoto, Masayuka Sanada, Еджи Такеда. “Операция широкой скорости внутреннего постоянного магнита синхронные двигатели с высокоэффективным текущим регулятором”. Транзакции IEEE на Промышленных Приложениях, Издании 30, Выпуске 4, июль/август 1994, стр 920–926.
[3] Муйанг Ли. “Ослабляющее поток управление для постоянного магнита синхронные двигатели на основе Z-исходных инверторов”. Магистерская диссертация, Университет Маркетт, e-Publications@Marquette, осень 2014 года.
[4] Briz, Фернандо, Майкл В. Дегнер и Роберт Д. Лоренц. "Анализ и проектирование текущих регуляторов, использующих комплексные векторы". Транзакции IEEE на Промышленных Приложениях, Издании 36, Выпуске 3, Могут/Июнь 2000, стр 817–825.
[5] Briz, Фернандо, и др. "Текущий и регулирование потока в ослабляющей поле операции [асинхронных двигателей]. "Транзакции IEEE на Промышленных Приложениях, Издании 37, Выпуске 1, Яне/Феврале 2001, стр 42–50.
Surface Mount PMSM | Flux-Based PM Controller | IM Controller | Interior PM Controller