Контроллер для основанного на потоке постоянного магнита синхронный двигатель
Powertrain Blockset / Движение / Контроллеры Электродвигателя
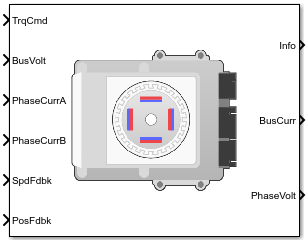
Блок Flux Based PM Controller реализует основанный на потоке, ориентированный на поле контроллер для внутреннего постоянного магнита синхронного двигателя (PMSM) с дополнительным контроллером скорости внешнего контура. Внутреннее управление крутящим моментом реализует стратегии достижения максимального крутящего момента на ампер (MTPA) и ослабления магнитного потока. Можно задать любого тип управления скоростью или крутящим моментом.
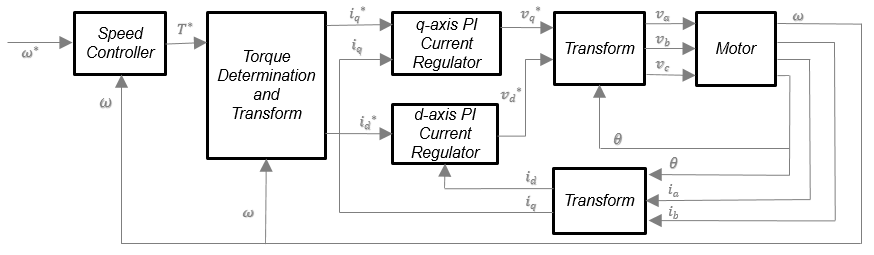
Flux Based PM Controller реализует уравнения для регулировки скорости, определения крутящего момента, регуляторов, преобразований координат и двигателей.
Фигура иллюстрирует информационный поток в блоке.
Блок реализует уравнения с помощью этих переменных.
| ω |
Скорость ротора |
| ω* |
Команда скорости ротора |
| T* |
Закрутите команду |
|
id i*d |
текущая d-ось d-ось текущая команда |
|
iq i*q |
текущая q-ось q-ось текущая команда |
|
vd, v*d |
напряжение d-оси команда напряжения d-оси |
|
vq v*q |
напряжение q-оси команда напряжения q-оси |
| va, vb, vc |
Фаза a Stator, b, c напряжения |
| ia, ib, ic |
Фаза a Stator, b, c токи |
Чтобы реализовать контроллер скорости, выберите параметр Control Type Speed Control. Если вы выбираете параметр Control Type Torque Control, блок не реализует контроллер скорости.
Контроллер скорости определяет команду крутящего момента путем реализования фильтра состояния и вычисления команд обратной связи и feedforward. Если вы не реализуете контроллер скорости, введите команду крутящего момента с блоком Flux Based PM Controller.
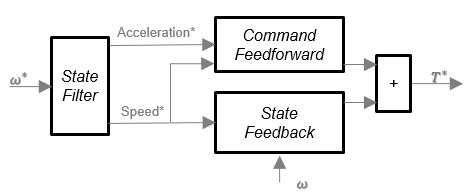
Фильтр состояния является фильтром lowpass, который генерирует ускоряющую команду на основе команды скорости. Дискретной формой характеристического уравнения дают:
Фильтр вычисляет усиление с помощью этого уравнения.
Уравнения используют эти переменные.
| EVsf |
Полоса пропускания фильтра команды скорости |
| Tsm |
Контроллер движения шаг расчета |
| Ksf |
Постоянная времени регулятора скорости |
Чтобы сгенерировать крутящий момент обратной связи состояния, блок использует отфильтрованный сигнал скоростной погрешности от фильтра состояния. Чтобы отфильтровать скорость, блок использует контроллер пропорционального интеграла (PI).
Уравнения используют эти переменные.
| ωm |
Скорость ротора |
| ω*m |
Команда скорости ротора |
| Tcmd |
Закрутите команду |
| Kpω |
Пропорциональная составляющая регулятора скорости |
| Kiω |
Интегральная составляющая регулятора скорости |
| Tsm |
Частота дискретизации регулятора скорости |
Чтобы сгенерировать крутящий момент прямого распространения состояния, блок использует отфильтрованную скорость и ускорение от фильтра состояния. Кроме того, вычисление крутящего момента прямого распространения использует инерцию, вязкое затухание и статическое трение. Чтобы достигнуть нулевой ошибки отслеживания, команда крутящего момента является суммой feedforward и команд крутящего момента обратной связи.
Команда крутящего момента прямого распространения использует это уравнение.
где:
| Jp |
Инерция ротора |
| Tcmd_ff |
Команда крутящего момента feedforward |
| Fs |
Статический постоянный момент трения |
| Fv |
Вязкий постоянный момент трения |
| Fs |
Статический постоянный момент трения |
| ωm |
Скорость ротора |
Блок использует интерполяционные таблицы, чтобы определить d-ось и q-ось текущие команды. Интерполяционные таблицы являются функциями механической скорости и крутящего момента. Чтобы определить интерполяционные таблицы, можно использовать внешний анализ конечных элементов (FEA) модели или динамометрические результаты испытаний.
Уравнения используют эти переменные.
| ωm |
Скорость ротора |
| Tref |
Закрутите команду |
| idref, iqref |
d-и текущая ссылка q-оси, соответственно |
Блок использует эти уравнения, чтобы вычислить напряжение в моторной системе координат.
Уравнения используют эти переменные.
|
ωm |
Скорость механического устройства ротора |
|
ωe | Ротор электрическая скорость |
|
Rs, Rr |
Сопротивление статора и обмоток ротора, соответственно |
|
iq, id |
q-и текущая d-ось, соответственно |
|
vq, vd |
q-и напряжение d-оси, соответственно |
| Ψq, Ψd |
q-и магнитный поток d-оси, соответственно |
| Tst |
Текущая частота дискретизации регулятора |
| Kid , Kiq |
d-и q-интегральная составляющая оси, соответственно |
| Kpd , Kpq |
d-и q-пропорциональная составляющая оси, соответственно |
Чтобы вычислить напряжения и токи в трехфазном сбалансированном (a, b) количества, двухфазная квадратура (α, β) количества, и вращающийся (d, q) системы координат, блок использует Преобразования Кларка и Парка.
В уравнениях преобразования.
| Преобразовать | Описание | Уравнения |
|---|---|---|
|
Кларк |
Преобразует сбалансированные трехфазные количества (a, b) в сбалансированные двухфазные квадратурные количества (α, β). | |
|
Парк |
Преобразует сбалансированные двухфазные ортогональные стационарные количества (α, β) в ортогональную систему координат вращения (d, q). | |
|
Инверсия Кларк |
Преобразует сбалансированные двухфазные квадратурные количества (α, β) в сбалансированные трехфазные количества (a, b). | |
|
Обратный парк |
Преобразует ортогональную систему координат вращения (d, q) в сбалансированные двухфазные ортогональные стационарные количества (α, β). |
Преобразования используют эти переменные.
| ωm |
Скорость ротора |
| P |
Пары полюса ротора |
| ωe |
Ротор электрическая скорость |
| Θe |
Ротор электрический угол |
| x |
Ток фазы или напряжение |
Блок использует токи фазы и напряжения фазы, чтобы оценить текущую шину DC. Положительный ток указывает на выброс батареи. Отрицательный ток указывает на заряд батареи.
Блок использует эти уравнения.
|
Загрузите степень | |
|
Исходная степень | |
|
Текущая шина DC | |
|
Предполагаемый крутящий момент ротора | |
|
Потери мощности для одного источника КПД, чтобы загрузить | |
|
Потери мощности для одного КПД загружают к источнику | |
|
Потери мощности для сведенного в таблицу КПД |
Уравнения используют эти переменные.
| va, vb, vc |
Фаза a Stator, b, c напряжения |
| vbus |
Предполагаемое напряжение на шине DC |
| ia, ib, ic |
Фаза a Stator, b, c токи |
| ibus |
Предполагаемая текущая шина DC |
| Eff |
Полный КПД инвертора |
| ωm |
Скорость механического устройства ротора |
| Lq, Ld |
q-и d-ось извилистая индуктивность, соответственно |
| Ψq, Ψd |
q-и магнитный поток d-оси, соответственно |
| iq, id |
q-и текущая d-ось, соответственно |
| λ |
Потокосцепление постоянного магнита |
| P |
Пары полюса ротора |
Задавать электрические потери, на вкладке Electrical Losses, для Parameterize losses by, избранной одной из этих опций.
| Установка | Блокируйте реализацию |
|---|---|
Single efficiency measurement | Электрическая потеря вычислила использование постоянного значения для КПД инвертора. |
Tabulated loss data | Электрическая потеря вычисляется в зависимости от частот вращения двигателя и крутящих моментов нагрузки. |
Tabulated efficiency data | Электрическая потеря вычислила с помощью КПД инвертора, который является функцией частот вращения двигателя и крутящих моментов нагрузки.
|
Для лучшей практики используйте Tabulated loss data вместо Tabulated efficiency data:
КПД заболевает заданный для нулевой скорости или нулевого крутящего момента.
Можно объяснить постоянные составляющие потерь, которые все еще присутствуют для нулевой скорости или крутящего момента.
[1] Ху, Dakai, Yazan Alsmadi и Луня Сюй. “Высокое качество нелинейное моделирование IPM на основе измеренного статора извилистое потокосцепление”. IEEE® Транзакции на промышленных приложениях, издании 51, № 4, июль/август 2015.
[2] Чен, Сяо, Джиэбин Ван, Bhaskar Сенатор, Панайотис Лазари, Tianfu Sun. “Высокочастотная и В вычислительном отношении Эффективная Модель для Внутренних Машин Постоянного магнита, Рассматривая Магнитное Насыщение, Пространственные Гармоники и Эффект Потери в железе”. Транзакции IEEE на Industrial Electronics, Издании 62, № 7, июль 2015.
[3] Оттоссон, J., М. Алэкула. “Компактное поле, ослабляющее реализацию контроллера”. Международный Симпозиум по Силовой электронике, Электрическим Дискам, Автоматизации и Движению, июль 2006.
Flux-Based PMSM | IM Controller | Interior PM Controller | Surface Mount PM Controller