Вращение системы координат кватерниона
rotationResult = rotateframe(quat,cartesianPoints)quat. Элементы кватерниона нормированы перед использованием во вращении.
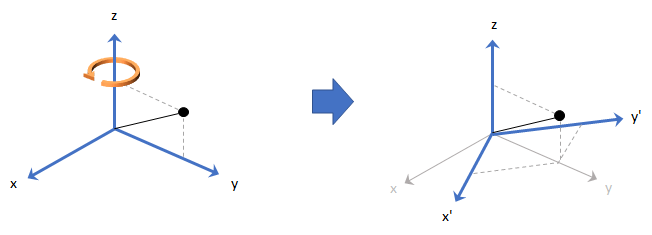
Вращение системы координат кватерниона повторно ссылается на точку, заданную в R3 путем вращения исходной системы отсчета согласно заданному кватерниону:
где q является кватернионом, * представляет спряжение, и u является точкой, чтобы вращаться в виде кватерниона.
Для удобства, rotateframe функционируйте берет точку в R3 и возвращает точку в R3. Учитывая вызов функции с некоторым произвольным кватернионом, q = a + b i + c j + d k и произвольная координата, [x, y, z],
point = [x,y,z]; rereferencedPoint = rotateframe(q,point)
rotateframe функция выполняет следующие операции:
Преобразует точку [x, y, z] к кватерниону:
Нормирует кватернион, q:
Применяет вращение:
Преобразует кватернион выход, vq, назад к R3