Exponenta Banner

Подавление помех в Simulink Используя нормированный адаптивный фильтр LMS

Создайте акустическую среду в Simulink

Адаптивные фильтры являются фильтрами, коэффициенты которых или веса изменяются в зависимости от времени, чтобы адаптироваться к статистике сигнала. Они используются во множестве полей включая коммуникации, средства управления, радар, гидролокатор, сейсмологию и биоинженерию.

В этой теме вы изучаете, как создать акустическую среду, которая симулирует и белый шум и окрашенный шум, добавленный к входному сигналу. Вы дальнейшее использование эта среда, чтобы создать модель, способную к адаптивному подавлению помех с помощью адаптивной фильтрации:

  1. В MATLAB® командная строка, введите dspanc.

    DSP System Toolbox™ Акустический пример Подавления помех открывается.

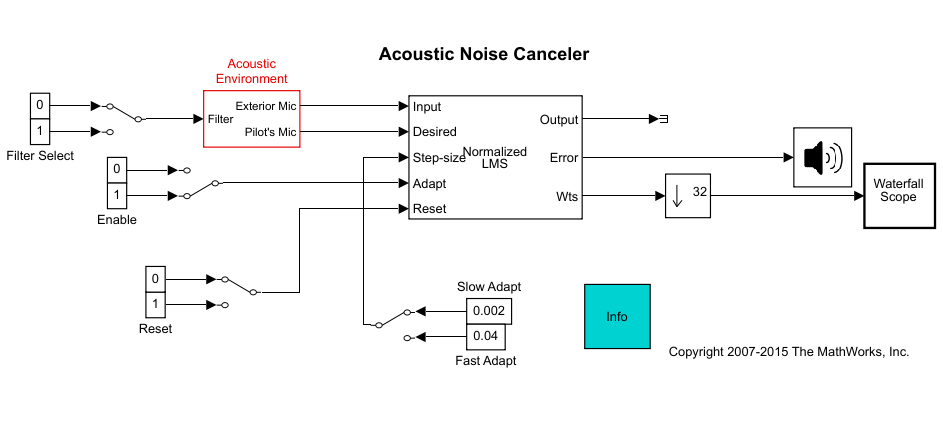
    Normalized LMS block has 5 inputs - input, desired, step size, adapt, and reset signal inputs. Acoustic environment subsystem block feeds the input and the desired signal. The LMS block generates output, error signal, and the weights. Output signal is connected to a terminator, Error signal to an Audio Device Writer, and the weights are downsampled by 32 and fed into a Waterfall Scope block.

  2. Скопируйте и вставьте подсистему под названием Акустическая Среда в новую модель.

  3. Дважды кликните Акустическую подсистему Среды.

    Гауссов шум используется, чтобы создать сигнал, отправленный во Внешний выходной порт Микрометра. Если вход к порту Filter изменяется с 0 до 1, блок Digital Filter изменяется с фильтра lowpass на полосовой фильтр. Отфильтрованный шумовой выход от блока Digital Filter добавляется, чтобы сигнализировать о прибытии из .wav файл, чтобы произвести сигнал, отправленный в выходной порт Микрометра Пилота.

Вы теперь создали акустическую среду. В следующих темах вы используете эту акустическую среду, чтобы произвести модель, способную к адаптивному подавлению помех.

Настройка фильтра LMS для адаптивного подавления помех

В предыдущей теме Создайте Акустическую Среду в Simulink, вы создали систему, которая произвела два выходных сигнала. Выход сигнала в порте Exterior Mic состоит из белого шума. Выход сигнала в порте Pilot's Mic состоит из цветного шума, добавленного к сигналу от .wav файл. В этой теме вы создаете адаптивный фильтр, чтобы удалить шум из сигнала Микрометра Пилота. Эта тема принимает, что вы работаете над Windows® операционная система:

  1. Если модель, в которой вы создали, Создает Акустическую Среду в Simulink, не открыто на вашем рабочем столе, можно открыть эквивалентную модель путем ввода

    ex_adapt1_audio

    в командной строке MATLAB.

  2. От библиотеки DSP System Toolbox Filtering, и затем от библиотеки Adaptive Filters, перетаскивают блок LMS Filter в модель, которая содержит Акустическую подсистему Среды.

  3. Дважды кликните блок LMS Filter. Установите параметры блоков можно следующим образом, и затем нажмите OK:

    • Algorithm = Normalized LMS

    • Filter length = 40

    • Step size (mu) = 0.002

    • Leakage factor (0 to 1) = 1

    Блок использует нормированный LMS-алгоритм, чтобы вычислить сорок коэффициентов фильтра. Установка параметра Leakage factor (0 to 1) на 1 средние значения, что текущие содействующие значения фильтра зависят от начальных условий фильтра и всех предыдущих входных значений.

  4. Перетащите следующие блоки в свою модель.

    БлокБиблиотекаКоличество

    Постоянный

    Simulink®/ Источники

    2

    Ручной переключатель

    Маршрутизация Simulink/Сигнала

    1

    Терминатор

    Simulink/Приемники

    1

    Downsample

    Операции сигнала

    1

    Средство записи аудио устройства

    Приемники

    1

    Осциллограф водопада

    Приемники

    1

  5. Соедините блоки так, чтобы ваша модель напомнила следующую фигуру.

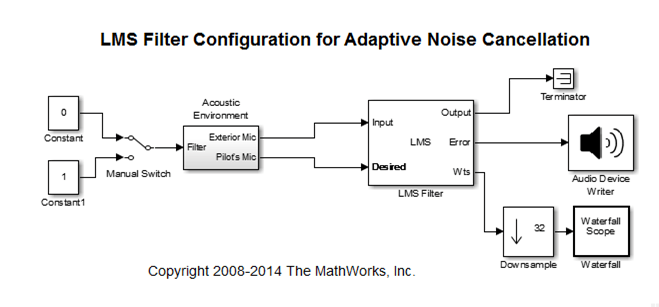
    Two constant blocks with a value of 0 and 1, respectively control the manual switch, which controls the Filter input of the Acoustic Environment. The acoustic environment block generates the input and the desired signal which are fed as inputs to the LMS Filter block. The LMS Filter block generates the output signal, error signal, and the weights. Output signal is connected to a terminator, Error signal to an Audio Device Writer, and the weights are downsampled by 32 and fed into a Waterfall Scope block.

  6. Дважды кликните блок Constant. Установите параметр Constant value на 0 и затем нажмите OK.

  7. Дважды кликните блок Downsample. Установите параметр Downsample factor, K на 32. Нажмите OK.

    Веса фильтра обновляются так часто, что существует очень мало изменения от одного обновления до следующего. Чтобы видеть более значимое изменение, необходимо проредить выход от порта Wts.

  8. Дважды кликните блок Waterfall Scope. Окно scope Waterfall открывается.

  9. Нажмите кнопку параметров Scope.

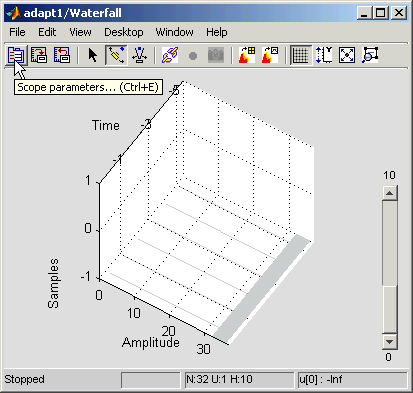
    Waterfall scope. The three axes in the waterfall plot are Time (ranging from -5 to 0), Samples (ranging from -1 to 1), and Amplitude (ranging from 0 to 30).

    Окно Parameters открывается.

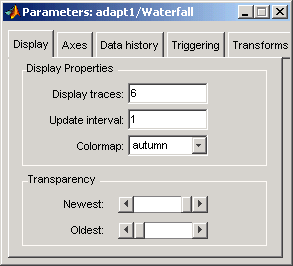
    In the Display tab of the Waterfall plot, the following Display properties are set: Display traces set to 6, Update interval set to 1, Colormap set to autumn. There are two additional Transparency related properties: Newest, Oldest.

  10. Кликните по вкладке Axes. Установите параметры можно следующим образом:

    • Y Min = -0.188

    • Y Max = 0.179

  11. Кликните по вкладке Data history. Установите параметры можно следующим образом:

    • History traces = 50

    • Data logging = All visible

  12. Закройте окно Parameters, оставив все другие параметры в их значениях по умолчанию.

    Вы можете должны быть настроить оси в окне scope Waterfall для того, чтобы просмотреть графики.

  13. Нажмите кнопку Fit to view в окне scope Waterfall. Затем перетащите оси, пока они не напомнят следующую фигуру.

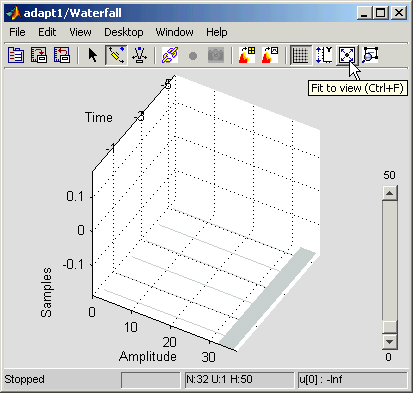
    Waterfall scope. The three axes in the waterfall plot are Time (ranging from -5 to 0), Samples (ranging from -0.2 to 0.2), and Amplitude (ranging from 0 to 30).

  14. Во вкладке Modeling нажмите Model Settings. В панели Solver, установленной параметры можно следующим образом, и затем, нажимают OK:

    • Stop time = inf

    • Type = Fixed-step

    • Solver = Discrete (no continuous states)

  15. Запустите симуляцию и просмотрите результаты в окне scope Waterfall. Можно также слушать симуляцию с помощью динамиков, присоединенных к компьютеру.

  16. Экспериментируйте с изменением Ручного Переключателя так, чтобы вход к Акустической подсистеме Среды был или 0 или 1.

    Когда значение 0, Гауссов шум в сигнале фильтруется фильтром lowpass. Когда значение равняется 1, шум фильтруется полосовым фильтром. Адаптивный фильтр может удалить шум в обоих случаях.

Вы теперь создали модель, способную к адаптивному подавлению помех. Адаптивный фильтр в вашей модели может отфильтровать и низкочастотный шум и шум в частотном диапазоне. В следующей теме Измените Адаптивные Параметры Фильтра Во время Симуляции модели, вы изменяете блок LMS Filter и изменяете его параметры в процессе моделирования.

Измените адаптивные параметры фильтра во время симуляции модели

В предыдущей теме, Настройке Фильтра LMS для Адаптивного Подавления помех, вы создали адаптивный фильтр и использовали его, чтобы удалить шум, сгенерированный Акустической подсистемой Среды. В этой теме вы изменяете адаптивный фильтр и настраиваете его параметры в процессе моделирования. Эта тема принимает, что вы работаете над операционной системой Windows:

  1. Если модель, в которой вы создали, Создает Акустическую Среду в Simulink, не открыто на вашем рабочем столе, можно открыть эквивалентную модель путем ввода 

    ex_adapt2_audio

    в командной строке MATLAB.

  2. Дважды кликните блок фильтра LMS. Установите параметры блоков можно следующим образом, и затем нажмите OK:

    • Specify step size via = Input port

    • Initial value of filter weights = 0

    • Установите флажок Adapt port.

    • Reset port = Non-zero sample

    Диалоговое окно Block Parameters: LMS Filter должно теперь выглядеть похожим на следующую фигуру.

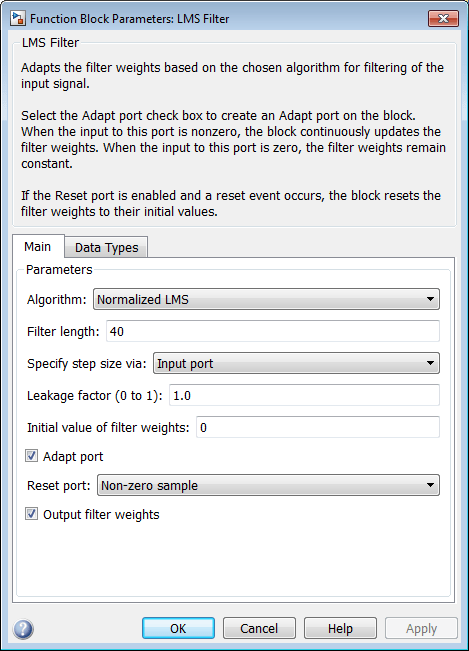
    LMS Filter block dialog parameters. In the Main tab, Algorithm is set to Normalized LMS, Filter length is set to 40, Specify step size via parameter is set to Input port, Leakage factor is set to 1.0, Initial values of filter weights is set to 0, Adapt port parameter is selected, Reset port is set to Non-zero sample, and Output filter weights parameter is selected.

    Неродной размер, Адаптируйтесь, и порты Reset появляются на блоке LMS Filter.

  3. Перетащите следующие блоки в свою модель.

    БлокБиблиотекаКоличество

    Постоянный

    Simulink/Источники

    6

    Ручной переключатель

    Маршрутизация Simulink/Сигнала

    3

  4. Соедините блоки как показано в следующем рисунке.

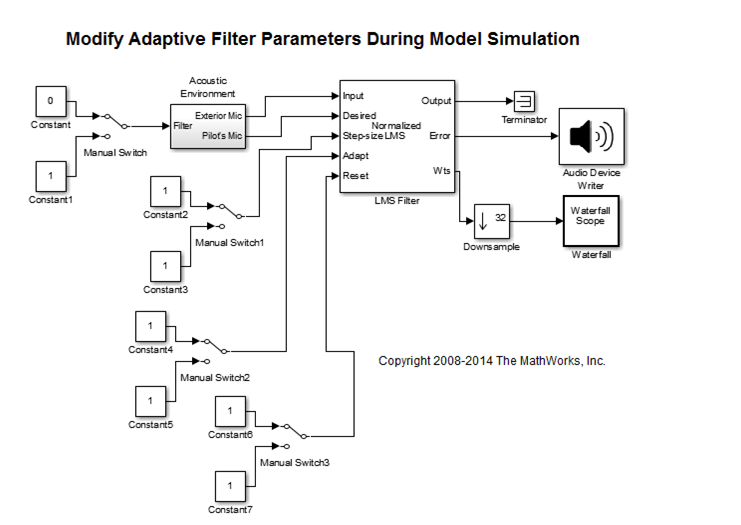
    Modify adaptive filter parameters during model simulation. Two constants 0 and 1 connect to the Filter input of the Acoustic Environment block through a manual switch. The two outputs of the Acoustic environment block, Exterior Mic and Pilot's mic feed in the Input and Desired signals in the Normalized LMS block. Two constant blocks feed the step size input of the LMS Filter block through a manual switch. Two constant blocks feed the adapt input of the LMS block through a manual switch. Two constant blocks feed the reset input of the LMS block through a manual switch. The three output signals of the LMS Filter block, Output signal, Error signal, and Weights connect to a terminator, Audio Device Writer, and a Waterfall scope block, respectively. There is a Downsample block (factor of 32) in between the Weights port and the Waterfall scope.

  5. Дважды кликните блок Constant2. Установите параметры блоков можно следующим образом, и затем нажмите OK:

    • Constant value = 0.002

    • Установите флажок Interpret vector parameters as 1-D.

    • Sample time (-1 for inherited) = inf

    • Output data type mode = Inherit via back propagation

  6. Дважды кликните блок Constant3. Установите параметры блоков можно следующим образом, и затем нажмите OK:

    • Constant value = 0.04

    • Установите флажок Interpret vector parameters as 1-D.

    • Sample time (-1 for inherited) = inf

    • Output data type mode = Inherit via back propagation

  7. Дважды кликните блок Constant4. Установите параметр Constant value на 0 и затем нажмите OK.

  8. Дважды кликните блок Constant6. Установите параметр Constant value на 0 и затем нажмите OK.

  9. Во вкладке Debug выберите Information Overlays> Nonscalar Signals и Signal Dimensions.

  10. Дважды кликните Руководство Switch2 так, чтобы вход к порту Adapt равнялся 1.

  11. Запустите симуляцию и просмотрите результаты в окне scope Waterfall. Можно также слушать симуляцию с помощью динамиков, присоединенных к компьютеру.

  12. Дважды кликните Ручной блок switch так, чтобы вход к Акустической подсистеме Среды равнялся 1. Затем дважды кликните Руководство Switch2 так, чтобы вход к порту Adapt к 0.

    Веса фильтра, отображенные в окне scope Waterfall, остаются постоянными. Когда вход к порту Adapt 0, веса фильтра не обновляются.

  13. Дважды кликните Руководство Switch2 так, чтобы вход к порту Adapt равнялся 1.

    Блок LMS Filter обновляет коэффициенты.

  14. Соедините блок Manual Switch1 с блоком Constant, который представляет 0.002. Затем измените вход в Акустическую подсистему Среды. Повторите эту процедуру с блоком Constant, который представляет 0.04.

    Вы видите, что система достигает устойчивого состояния быстрее, когда размер шага больше.

  15. Дважды кликните блок Manual Switch3 так, чтобы вход к порту Reset равнялся 1.

    Блок сбрасывает веса фильтра к их начальным значениям. В диалоговом окне Block Parameters: LMS Filter, из списка Reset port, вы выбрали Non-zero sample. Это означает, что любой ненулевой вход к порту Reset инициировал операцию сброса.

Вы теперь экспериментировали с адаптивным подавлением помех с помощью блока LMS Filter. Вы настроили параметры своего адаптивного фильтра и просмотрели эффекты ваших изменений, в то время как модель запускалась.

Для получения дополнительной информации об адаптивных фильтрах, смотрите следующие страницы с описанием блока:

Ссылки

[1] Hayes, Монсон Х., Статистическая Цифровая обработка сигналов и Моделирование. Хобокен, NJ: John Wiley & Sons, 1996, pp.493–552.

[2] Haykin, Саймон, адаптивная теория фильтра. Верхний Сэддл-Ривер, NJ: Prentice-Hall, Inc., 1996.

Похожие темы

Документация DSP System Toolbox

Поддержка