Работа с отрицательными процентными ставками Используя функции

Опции моделирования процентной ставки для отрицательных уровней

Financial Instruments Toolbox™ вычисляет цены на дно, этажи и swaptions при моделировании для отрицательных процентных ставок с помощью Нормальной модели энергозависимости, переключенной модели Black или переключенной модели SABR:

Нормальная модель энергозависимости (модель Bachelier) для опций процентной ставки, чтобы обработать отрицательные уровни со следующим:
Переключенная модель Black и переключенная модель SABR для опций процентной ставки с помощью дополнительного Shift аргумент, чтобы обработать отрицательные уровни со следующим:
- blackvolbysabr (Переключенный SABR)
- optsensbysabr (Переключенный SABR)
- swaptionbyblk (Переключенный Черный цвет)
- capbyblk (Переключенный Черный цвет)
- floorbyblk (Переключенный Черный цвет)
- capvolstrip (Переключенный Черный цвет)
- floorvolstrip (Переключенный Черный цвет)

Моделирование отрицательных уровней

Исходные авторы модели SABR обеспечили закрытое приближение формы подразумеваемой Черной энергозависимости в терминах параметров модели SABR (известный как формулу “Хейгана”), так, чтобы цена опции могла быть вычислена путем вставки вычисленной Черной энергозависимости SABR в Черную формулу:

$C a l l (K, T) = B l a c k_{c a l l} (F, K, r, T, σ_{B l a c k} (α, β, ρ, ν, F, K, T))$

Однако эти методы начали ломаться с введением отрицательных процентных ставок, из-за предположения о модели Black, что базовые уровни логарифмически нормально распределяются (и поэтому не может быть отрицательным).

Кроме того, даже когда базовый уровень положителен, закрытое приближение формы SABR подразумевало, что Черная энергозависимость (Хейган и др., 2002), как известно, становится все больше неточной как нуль подходов забастовки. Даже не пересекая нулевой контур забастовки, подразумеваемая плотность вероятности базового уровня при истечении опции может стать отрицательной в низких положительных забастовках, несмотря на то, что плотности вероятности ясно не должны быть отрицательными:

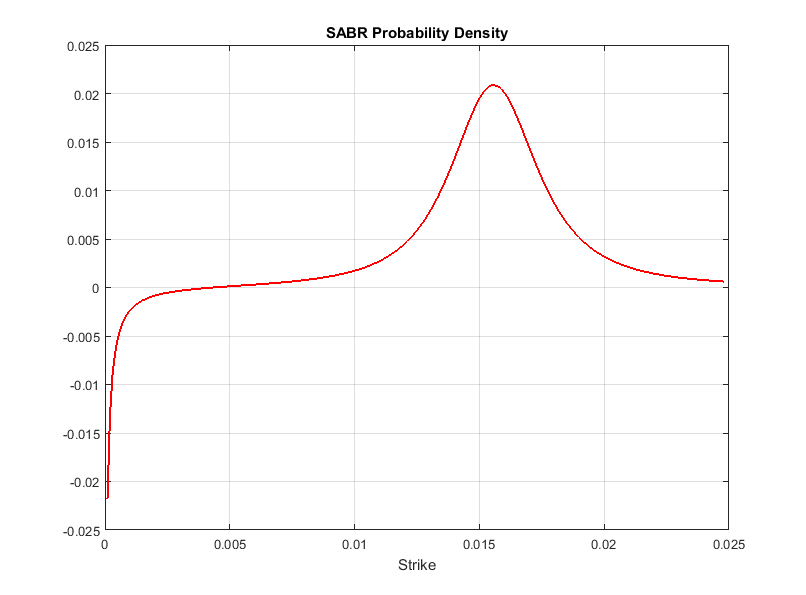
Опции с отрицательными забастовками не могут быть представлены Черными колебаниями. Чтобы работать вокруг этой проблемы, рынок начал заключать в кавычки дно, пол и swaption цены также или в терминах Нормальных колебаний или в терминах Переключенных Черных колебаний. Вместо модели Black оба типа колебаний прибывают из альтернативных моделей, которые позволяют отрицательные уровни.

Нормальная модель

Нормальные колебания сопоставлены с моделью Normal (также известный как модель Bachelier):

где базовые уровни приняты, чтобы быть нормально распределенными. В отличие от этого, в логарифмически нормальной модели (где уровни имеют нижнюю границу), уровни в модели Normal могут быть и бесконечно положительными и бесконечно отрицательными.

Переключенный черный цвет

Переключенные Черные колебания сопоставлены с моделью Shifted Black (также известный как модель “Displaced Diffusion” или “Shifted Lognormal”):

Модель Shifted Black является по существу тем же самым как моделью Black, за исключением того, что это моделирует перемещения (F + Shift) как базовый актив вместо F (где F является прямым уровнем подкачки в случае swaptions и форвардным курсом в случае caplets и floorlets). Так, модель Shifted Black позволяет отрицательные уровни с фиксированной отрицательной нижней границей, заданной суммой сдвига, то есть, нулевая нижняя граница модели Black была смещена.

Переключенный SABR

Введение отрицательных процентных ставок также призвало к обновлению в методе для интерполяции колебаний, заключенных в кавычки на рынке. Следующее показывает связи между колебаниями и моделями SABR:

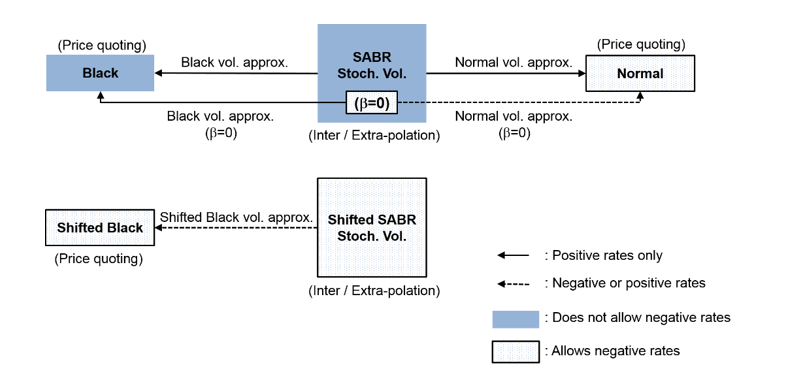
Как показано Черные и Нормальные приближения энергозависимости позволяют вам использовать модель SABR с опцией модели Black и Normal, оценивая формулы. Однако несмотря на то, что сама модель Normal позволяет отрицательные уровни, и модель SABR имеет подразумеваемое Нормальное приближение энергозависимости, базовые движущие силы модели SABR не позволяют отрицательные уровни, если β = 0. В модели Shifted SABR Переключенное Черное приближение энергозависимости может использоваться, чтобы позволить отрицательные уровни с фиксированной отрицательной нижней границей, заданной суммой сдвига.

Подразумеваемая нормальная энергозависимость и SABR

Можно вычислить подразумеваемую Нормальную энергозависимость в терминах параметров модели SABR для любого β = 0 (Нормальный SABR), или любое другое значение β, позволенного моделью SABR (0 ≤ β ≤ 1) использование normalvolbysabr.

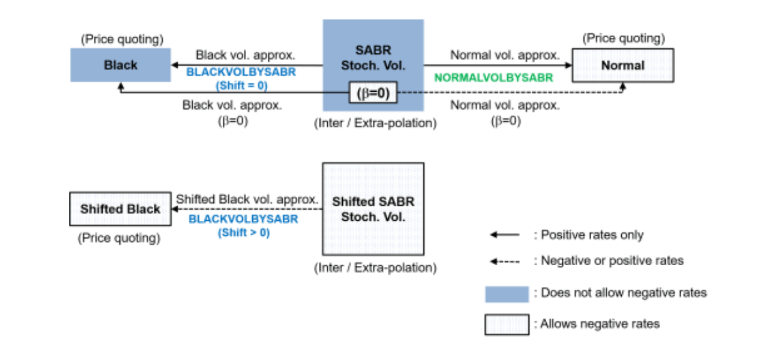
normalvolbysabrвычисляет подразумеваемую Нормальную энергозависимость σ _N в терминах параметров модели SABR. Используя normalvolbysabr чтобы вычислить σ _N, вы можете затем вы это с другими функциями для оценки модели Normal (например, capbynormal, floorbynormal, и swaptionbyblk).

Документация