Ограниченная минимизация Используя patternsearch и Optimize Задача Live Editor

В этом примере показано, как решить ограниченную задачу минимизации с помощью и Оптимизировать задачи Live Editor, которая предлагает визуальный подход и командную строку.

Описание проблемы

Проблема включает использующие линейные и нелинейные ограничения при минимизации нелинейной функции с patternsearch. Целевая функция

F(x)=12xTHx+fTx,

где

H = [36 17 19 12  8 15; 
     17 33 18 11  7 14; 
     19 18 43 13  8 16;
     12 11 13 18  6 11; 
      8  7  8  6  9  8; 
     15 14 16 11  8 29];

f = [ 20 15 21 18 29 24 ]';
 
F = @(x)0.5*x'*H*x + f'*x;

Эта целевая функция также включена с вашим программным обеспечением в файле lincontest7.m.

Линейные ограничения

A⋅x≤b,Aeq⋅x=beq,

где 

A = [-8 7 3 -4 9 0];
b = 7;
Aeq = [7 1 8 3 3 3;
      5 0 -5 1 -5 8;
     -2 -6 7 1 1 9;
      1 -1 2 -2 3 -3];
beq = [84 62 65 1]';

Введите предыдущие секции кода, чтобы получить переменные задачи в вашу рабочую область перед продолжением.

Решите Используя patternsearch в оптимизируют задачу Live Editor

  1. Создайте новый live скрипт путем нажатия кнопки New Live Script в разделе File по вкладке Home.

    New Live Script button

  2. Вставьте Оптимизировать задачу Live Editor. Кликните по вкладке Insert и затем, в разделе Code, выберите Task > Optimize.

    Insert Optimize Live Editor task.

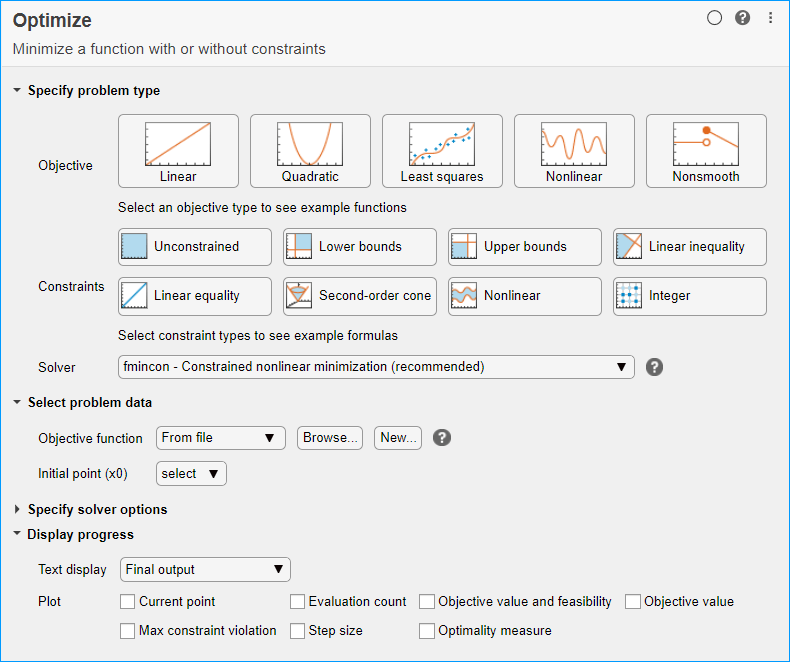
    Optimize Live Editor task initial screen

  3. Задайте проблемный тип

    В разделе Specify problem type задачи нажмите кнопку Objective > Nonlinear.

  4. Нажмите кнопки Constraints > Linear inequality и Linear equality.

  5. Выберите Solver > patternsearch - Pattern search.

  6. Выберите Problem Data

    Введите переменные задачи в раздел Select problem data задачи. Чтобы задать целевую функцию, выберите Objective function > Function handle и выберите F.

  7. Установите ограничения неравенства на A и b. Установите ограничения равенства на Aeq и beq.

  8. Чтобы установить начальную точку, сначала необходимо создать новый раздел выше задачи. Для этого нажмите кнопку Section Break на вкладке Insert. В новом разделе выше задачи введите следующий код для начальной точки.

    x0 = [2 1 0 9 1 0]';

  9. Запустите раздел, чтобы поместить x0 в рабочую область. Чтобы запустить раздел, установите курсор в раздел и нажмите Ctrl+Enter или кликните по синей чередуемой панели слева от номера строки.

  10. В разделе Select problem data задачи, набор x0 как начальная точка.

  11. Задайте опции решателя

    Поскольку эта проблема линейно ограничивается, задайте дополнительную опцию решателя. Расширьте раздел Specify solver options задачи, и затем нажмите кнопку Add. Установите Poll settings > Poll method на GSSPositiveBasis2N. Для получения дополнительной информации о КПД методов опроса GSS для линейно ограниченных проблем, смотрите, Сравнивают КПД Опций Опроса.

  12. Опции дисплея аппарата

    В разделе Display progress задачи выберите функции построения графика Mesh size и Best value.

    Ваша настройка выглядит так:

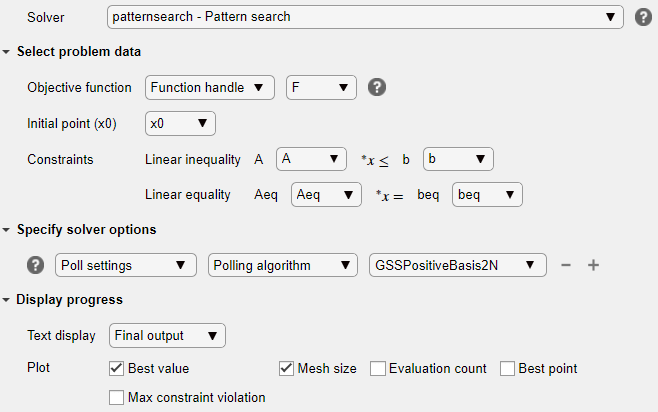
    patternsearch solver, function handle F, initial point x0, linear constraints A, b, Aeq, beq, poll algorithm GSSPositiveBasis2N, plots Best value and Mesh size

  13. Запустите решатель и исследуйте результаты

    Чтобы запустить решатель, кликните по кнопке ⁝ опций в правом верхнем из окна задачи и выберите Run Section.

    Run the solver; the keyboard equivalent is Ctrl+Enter.

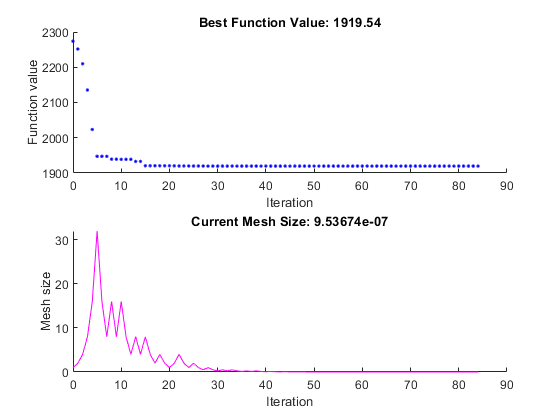
    Графики появляются в отдельном окне рисунка и в области вывода задачи.

    Plots show the objective function value decreasing with iterations to 1919 and the mesh size eventually decreasing below 1e-6.

  14. Чтобы получить точку решения и значение целевой функции в решении, посмотрите во главе задачи.

    Optimize returns "solution" and "objectiveValue" variables

    Optimize Задача Live Editor возвращает решение в переменной под названием solution и возвращает значение целевой функции в переменной под названием objectiveValue. Просмотрите эти значения путем ввода следующего кода в разделе ниже задачи и затем выполнения раздела, или путем ввода кода в MATLAB® командная строка.

    disp(solution)
        8.5165
   -6.1094
    4.0989
    1.2877
   -4.2348
    2.1812
    disp(objectiveValue)
       1.9195e+03

  15. Включайте нелинейные ограничения

    Добавьте следующие нелинейные ограничения в проблему.

    −1.5+x1x2+x1−x2≤0−x1x2−10≤0.

    Чтобы включать эти ограничения, сначала нажмите кнопку Constraints > Nonlinear.

    Include a nonlinear constraint.

  16. В разделе Select problem data, под Constraints, выбирают Nonlinear > Local function и затем нажимают кнопку New. Функция появляется в новом разделе ниже задачи. Отредактируйте получившийся код, чтобы содержать следующие линии.

    function [c, ceq] = double_ineq(x)
c = [-1.5 + x(1)*x(2) + x(1) - x(2);
    -x(1)*x(2) - 10];
ceq = [];
end

  17. В ограничительном разделе Nonlinear выберите double_ineq.

  18. Нелинейные ограничительные причины алгоритма patternsearch взять много вычислений функции. В разделе Specify solver options кликните по знаку "плюс" справа от текущих опций, чтобы отобразить дополнительные опции. Затем увеличьте максимальный предел вычисления функции 5e4.

    Max function evals = 5e4

  19. Запустите задачу снова, чтобы повторно выполнить оптимизацию.

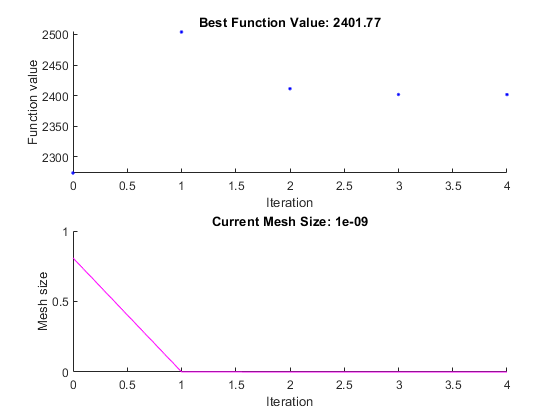
    The top plot shows four iterations with a best function value of 2401.77. The bottom plot shows the mesh size decreasing to 1e-9.

  20. Просмотрите значение функции решения и целевой функции.

    disp(solution)
        7.2083
   -1.3873
    4.9579
   -3.1393
   -3.1843
    4.7457
    disp(objectiveValue)
       2.4018e+03

Значение целевой функции выше, чем значение в проблеме без нелинейных ограничений. Предыдущее решение не выполнимо относительно нелинейных ограничений.

Графики показывают многим меньше итераций, чем прежде, потому что нелинейный ограничительный алгоритм изменяется patternsearch алгоритм, чтобы включать другой внешний контур, чтобы решить модифицированную задачу. Внешний контур уменьшает модификацию до проблемы в каждой главной итерации. В этом случае алгоритм делает только четыре внешних итерации. Для получения дополнительной информации алгоритма смотрите Нелинейный Ограничительный Алгоритм решателя.

Решите Используя patternsearch в командной строке

Чтобы решить исходную задачу (только линейные ограничения) в командной строке, выполните следующий код.

x0 = [2 1 0 9 1 0]';
options = optimoptions('patternsearch',...
    'PollMethod','GSSPositiveBasis2N',...
    'PlotFcn',{'psplotbestf','psplotmeshsize'});
lb = [];
ub = [];
nonlcon = [];
[x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Optimization terminated: mesh size less than options.MeshTolerance.

x =

    8.5165
   -6.1094
    4.0989
    1.2877
   -4.2348
    2.1812


fval =

   1.9195e+03

patternsearch генерирует первую пару графиков, показанных в Оптимизировать примере задачи Live Editor.

Чтобы включать нелинейные ограничения, сохраните следующий код в файл с именем double_ineq.m на пути MATLAB.

function [c, ceq] = double_ineq(x)
c = [-1.5 + x(1)*x(2) + x(1) - x(2);
    -x(1)*x(2) - 10];
ceq = [];
end

Чтобы позволить решателю выполнение до завершения с нелинейными ограничениями, увеличьте позволенное число вычислений функции.

options.MaxFunctionEvaluations = 5e4;

Решите задачу включая нелинейные ограничения.

nonlcon = @double_ineq;
[x,fval] = patternsearch(F,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    7.2083
   -1.3873
    4.9579
   -3.1393
   -3.1843
    4.7457


fval =

   2.4018e+03

patternsearch также генерирует вторую пару графиков, показанных в Оптимизировать примере задачи Live Editor.

И Оптимизировать задача Live Editor и командная строка позволяют вам формулировать и решать проблемы, и они дают идентичные результаты. Командная строка более оптимизирована, но обеспечивает меньше справки для выбора решателя, подготовки проблема и выбора опций, таких как функции построения графика. Можно также запустить, использование задач Оптимизируют, и затем генерируют код для использования командной строки, когда в Решают Ограниченную Нелинейную задачу, Основанную на решателе.

Смотрите также

Похожие темы

Документация Global Optimization Toolbox

Поддержка

Для просмотра документации необходимо авторизоваться на сайте