В этом примере показано, как решить ограниченную нелинейную задачу с помощью решателя Optimization Toolbox™. Пример демонстрирует типичный рабочий процесс: создайте целевую функцию, создайте ограничения, решите задачу и исследуйте результаты.
Этот пример обеспечивает два подхода к решению задачи. Каждый использует Оптимизировать задачу Live Editor, визуальный подход. Другое использование MATLAB® командная строка, основанный на тексте подход. Можно также решить этот тип проблемы с помощью подхода, основанного на проблеме; смотрите Решают Ограниченную Нелинейную задачу, Основанную на проблеме.
Проблема состоит в том, чтобы минимизировать функцию Розенброка
по unit disk, то есть, диску радиуса 1 с центром в начале координат. Другими словами, найдите x, который минимизирует функциональный f (x) на множестве . Этой проблемой является минимизация нелинейной функции с нелинейным ограничением.
Примечание
Функция Розенброка является стандартной тестовой функцией в оптимизации. Это имеет уникальное минимальное значение 0 достигнутых в точке [1,1]. Нахождение минимума является проблемой для некоторых алгоритмов, потому что функция имеет неглубокий минимум в очень кривом овраге. Решением для этой проблемы не является в точке [1,1] потому что та точка не удовлетворяет ограничению.
Этот рисунок показывает два представления функции Розенброка на единичном диске. Вертикальная ось имеет логарифмическое масштабирование; другими словами, график показывает журнал (1+f (x)). Линии контура лежат ниже графика поверхности.
Функция Розенброка, масштабируемая журналом: два представления
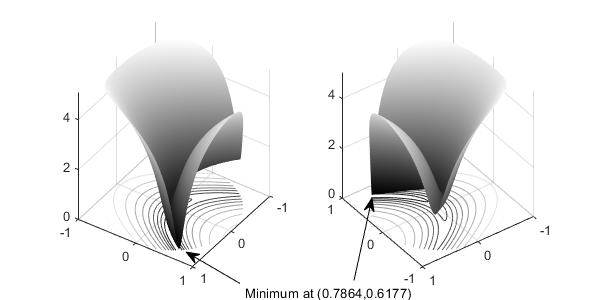
Функциональный f (x) называется целевой функцией. Целевая функция является функцией, которую вы хотите минимизировать. Неравенство называется ограничением. Ограничения ограничивают набор x, по которому решатель ищет минимум. У вас может быть любое количество ограничений, которые являются неравенствами или равенствами.
Все оптимизационные функции Optimization Toolbox минимизируют целевую функцию. Чтобы максимизировать функциональный f, примените стандартную программу оптимизации, чтобы минимизировать –f. Для получения дополнительной информации о максимизации, смотрите Максимизацию Цели.
Оптимизировать задача Live Editor позволяет вам настроить и решить задачу с помощью визуального подхода.
Создайте новый live скрипт путем нажатия кнопки New Live Script на разделе File вкладки Home.
Вставьте Оптимизировать задачу Live Editor. Кликните по вкладке Insert и затем, в разделе Code, выберите Task > Optimize.
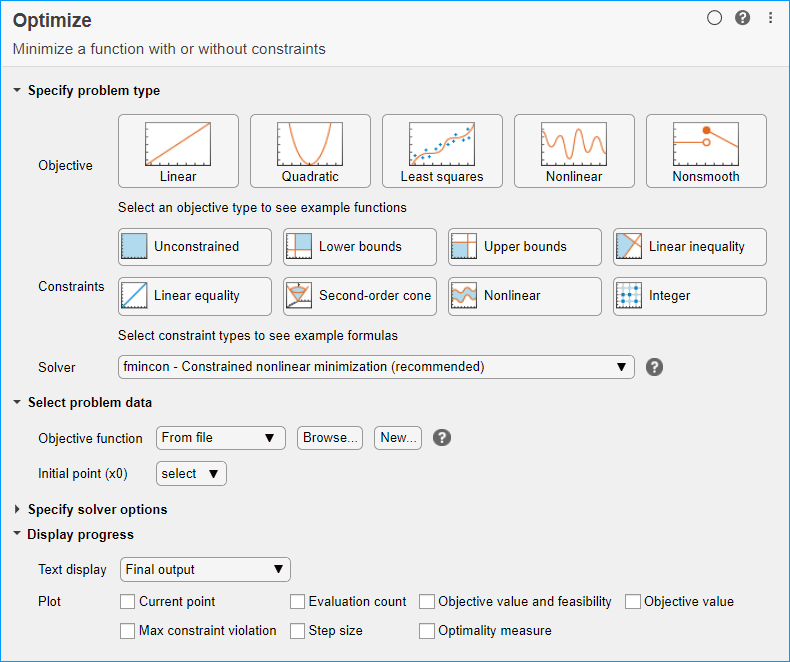
В разделе Specify problem type задачи выберите Objective > Nonlinear и Constraints > Nonlinear. Задача выбирает решатель fmincon - Constrained nonlinear minimization.
Включайте функцию Розенброка как целевую функцию. В разделе Select problem data задачи выберите Objective function > Local function и затем нажмите кнопку New.... Новая локальная функция появляется в разделе ниже задачи.
function f = objectiveFcn(optimInput) % Example: % Minimize Rosenbrock's function % f = 100*(y - x^2)^2 + (1 - x)^2 % Edit the lines below with your calculation x = optimInput(1); y = optimInput(2); f = 100*(y - x^2)^2 + (1 - x)^2; end
Эта функция реализует функцию Розенброка.
В разделе Select problem data задачи выберите Objective function > objectiveFcn.
Поместите начальную точку x0 = [0;0] в рабочее пространство MATLAB. Вставьте новый раздел выше Оптимизировать задачи путем нажатия на задачу, затем нажатия кнопки Section Break на вкладке Insert. В новом разделе выше задачи введите следующий код для начальной точки.
x0 = [0;0];
Запустите раздел путем нажатия Ctrl+Enter. Это действие помещает x0 в рабочую область.
В разделе Select problem data задачи выберите Initial point (x0) > x0.
В разделе Select problem data выберите Constraints > Nonlinear > Local function и затем нажмите кнопку New.... Новая локальная функция появляется ниже предыдущей локальной функции.
Отредактируйте новую локальную функцию можно следующим образом.
function [c,ceq] = unitdisk(x) c = x(1)^2 + x(2)^2 - 1; ceq = [ ]; end
В разделе Select problem data выберите unitdisk как ограничительная функция.
Чтобы контролировать прогресс решателя, в разделе Display progress задачи, выбирают Text display > Each iteration. Кроме того, выберите Objective value and feasibility для графика.

Чтобы запустить решатель, кликните по кнопке ⁝ опций в правом верхнем из окна задачи и выберите Run Section. График появляется в отдельном окне рисунка и в области вывода.
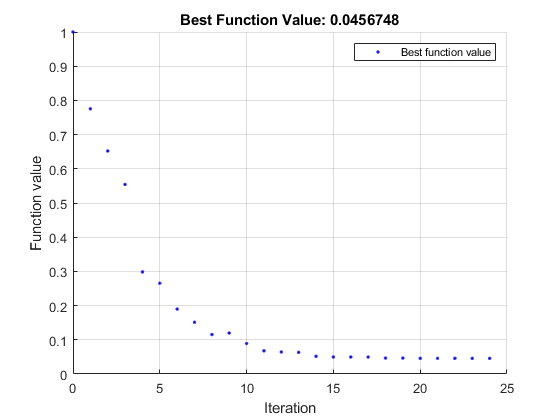
Область вывода показывает, что таблица итераций, обсужденных в, Интерпретирует Результат.
Чтобы найти решение, посмотрите во главе задачи.
![]()
Решатель помещает переменные solution и objectiveValue в рабочей области. Просмотрите их значения путем вставки нового разрыва раздела ниже задачи и ввода этих линий.

Запустите раздел путем нажатия Ctrl+Enter.
![solution = [0.7864,0.6177]. objectiveValue = 0.0457.](optimizelet_viewsolution_result.png)
Понять fmincon процесс для получения результата, смотрите, Интерпретируют Результат.
Отобразить код, которые Оптимизируют, генерирует, чтобы решить задачу, кликнуть по кнопке ⁝ опций в правом верхнем из окна задачи и выбрать Controls and Code.
В нижней части задачи появляется следующий код.
% Set nondefault solver options options = optimoptions('fmincon','Display','iter','PlotFcn',... 'optimplotfvalconstr'); % Solve [solution,objectiveValue] = fmincon(@objectiveFcn,x0,[],[],[],[],[],[],... @unitdisk,options);
Этот код является кодом, который вы используете, чтобы решить задачу в командной строке, аналогичной описанному затем.
Первый шаг в решении задачи оптимизации в командной строке должен выбрать решатель. Консультируйтесь с Таблицей решений Оптимизации. Для проблемы с нелинейной целевой функцией и нелинейным ограничением, обычно вы используете fmincon решатель.
Консультируйтесь fmincon страница ссылки на функцию. Синтаксис решателя следующие.
[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
fun и nonlcon входные параметры представляют целевую функцию и нелинейные ограничительные функции, соответственно.
Опишите свою проблему можно следующим образом:
Задайте целевую функцию на языке MATLAB как файл функции или анонимная функция. Этот пример использует файл функции.
Задайте ограничения как отдельный файл или анонимную функцию.
Файл функции является текстовым файлом, который содержит команды MATLAB и имеет дополнительный .m. Создайте файл функции в любом текстовом редакторе или используйте встроенный в MATLAB редактор, как в этом примере.
В командной строке, введите:
edit rosenbrockВ редакторе MATLAB, введите:
%% ROSENBROCK(x) expects a two-column matrix and returns a column vector % The output is the Rosenbrock function, which has a minimum at % (1,1) of value 0, and is strictly positive everywhere else. function f = rosenbrock(x) f = 100*(x(:,2) - x(:,1).^2).^2 + (1 - x(:,1)).^2;
Примечание
rosenbrock векторизованная функция, которая может вычислить значения для нескольких точек целиком. Смотрите Векторизацию. Векторизованная функция является лучшей для графического вывода. Для невекторизованной версии, введите:
%% ROSENBROCK1(x) expects a two-element vector and returns a scalar % The output is the Rosenbrock function, which has a minimum at % (1,1) of value 0, and is strictly positive everywhere else. function f = rosenbrock1(x) f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
Сохраните файл с именем rosenbrock.m.
Ограничительные функции имеют форму c (x) ≤ 0 или ceq (x) = 0. Ограничение не находится в форме, которую обрабатывает решатель. Чтобы иметь правильный синтаксис, переформулируйте ограничение как .
Синтаксис для нелинейных ограничений возвращает и ограничения равенства и ограничения неравенства. Этот пример включает только ограничение неравенства, таким образом, необходимо передать пустой массив [] как ограничение равенства функционируют ceq.
Учитывая эти соображения, запишите файл функции для нелинейного ограничения.
Создайте файл с именем unitdisk.m содержа следующий код:
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];Сохраните файл unitdisk.m.
Теперь, когда вы задали цель и ограничительные функции, создайте другой fmincon входные параметры.
Создайте опции для fmincon использовать 'optimplotfvalconstr' функция построения графика и возвратить итеративное отображение.
options = optimoptions('fmincon',... 'PlotFcn','optimplotfvalconstr',... 'Display','iter');
Создайте начальную точку.
x0 = [0 0];
Создайте пустые записи для ограничений, которые не использует этот пример.
A = []; b = []; Aeq = []; beq = []; lb = []; ub = [];
Решите задачу путем вызова fmincon.
[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 3 1.000000e+00 0.000e+00 2.000e+00
1 13 7.753537e-01 0.000e+00 6.250e+00 1.768e-01
2 18 6.519648e-01 0.000e+00 9.048e+00 1.679e-01
3 21 5.543209e-01 0.000e+00 8.033e+00 1.203e-01
4 24 2.985207e-01 0.000e+00 1.790e+00 9.328e-02
5 27 2.653799e-01 0.000e+00 2.788e+00 5.723e-02
6 30 1.897216e-01 0.000e+00 2.311e+00 1.147e-01
7 33 1.513701e-01 0.000e+00 9.706e-01 5.764e-02
8 36 1.153330e-01 0.000e+00 1.127e+00 8.169e-02
9 39 1.198058e-01 0.000e+00 1.000e-01 1.522e-02
10 42 8.910052e-02 0.000e+00 8.378e-01 8.301e-02
11 45 6.771960e-02 0.000e+00 1.365e+00 7.149e-02
12 48 6.437664e-02 0.000e+00 1.146e-01 5.701e-03
13 51 6.329037e-02 0.000e+00 1.883e-02 3.774e-03
14 54 5.161934e-02 0.000e+00 3.016e-01 4.464e-02
15 57 4.964194e-02 0.000e+00 7.913e-02 7.894e-03
16 60 4.955404e-02 0.000e+00 5.462e-03 4.185e-04
17 63 4.954839e-02 0.000e+00 3.993e-03 2.208e-05
18 66 4.658289e-02 0.000e+00 1.318e-02 1.255e-02
19 69 4.647011e-02 0.000e+00 8.006e-04 4.940e-04
20 72 4.569141e-02 0.000e+00 3.136e-03 3.379e-03
21 75 4.568281e-02 0.000e+00 6.440e-05 3.974e-05
22 78 4.568281e-02 0.000e+00 8.000e-06 1.084e-07
23 81 4.567641e-02 0.000e+00 1.601e-06 2.793e-05
24 84 4.567482e-02 0.000e+00 2.023e-08 6.916e-06
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
x =
0.7864 0.6177
fval =
0.0457
Выходное сообщение говорит вам, что поиск ограниченного оптимума, законченного, потому что производная целевой функции - почти 0 в направлениях, позволенных ограничением, и что ограничению удовлетворяют к требуемой точности. Несколько фраз в сообщении содержат ссылки на большую информацию о терминах, использованных в сообщении. Для получения дополнительной информации об этих ссылках, смотрите Расширенные Выходные сообщения.
Таблица итерации и в области вывода задачи Live Editor и в командном окне MATLAB показывает, как MATLAB искал минимальное значение функции Розенброка на единичном диске. Ваша таблица может отличаться, в зависимости от версии тулбокса и вычислительной платформы. Следующее описание применяется к таблице, показанной в этом примере.
Первый столбец, пометил Iter, номер итерации от 0 до 24. fmincon взял 24 итерации, чтобы сходиться.
Второй столбец, пометил F-count, сообщает, что накопительное число раз вычислений функции Розенброка было оценено. Итоговая строка показывает F-count из 84, указывая на это fmincon функция оцененного Розенброка 84 раза в процессе нахождения минимума.
Третий столбец, пометил f(x), отображает значение целевой функции. Окончательное значение, 4.567482e-2, минимум, о котором сообщают в Оптимизировать запуске, и в конце выходного сообщения в Командном окне.
Четвертый столбец, Feasibility, 0 для всех итераций. Этот столбец показывает значение ограничительной функции unitdisk в каждой итерации, где ограничение положительно. Поскольку значение unitdisk было отрицательно во всех итерациях, каждая итерация удовлетворила ограничению.
Другие столбцы таблицы итерации описаны в Итеративном Отображении.