В этом примере показано, как найти локальный минимум функции с помощью симулированного отжига. Пример представляет два подхода для минимизации: работа в командной строке и использование Оптимизировать задача Live Editor.
Пятая функция Де Йонга является двумерной функцией со многими (25) локальные минимумы. В следующем графике это неясно, какой из этих локальных минимумов является глобальным минимумом.
dejong5fcn

Много стандартных алгоритмов оптимизации становятся всунутыми локальными минимумами. Поскольку симулированный алгоритм отжига выполняет широкий случайный поиск, шанс того, чтобы быть захваченным в локальном минимуме уменьшен.
Note:Because симулировал, отжигая генераторы случайных чисел использования, каждый раз, когда вы запускаете этот алгоритм, можно получить различные результаты. Смотрите Воспроизводят Ваши Результаты для получения дополнительной информации.
Чтобы запустить симулированный алгоритм отжига без ограничений, вызвать simulannealbnd в командной строке с помощью целевой функции в dejong5fcn.m, ссылаемый анонимной функцией @dejong5fcn в следующем коде.
rng(10,'twister') % for reproducibility fun = @dejong5fcn; [x,fval] = simulannealbnd(fun,[0 0])
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-16.1292 -15.8214
fval =
6.9034В результатах:
x конечная точка, возвращенная алгоритмом.
fval значение целевой функции в конечной точке.
Можно также запустить минимизацию с помощью Оптимизировать задачи Live Editor, которая обеспечивает визуальный подход.
Создайте новый live скрипт путем нажатия кнопки New Live Script в разделе File по вкладке Home.
Вставьте Оптимизировать задачу Live Editor. Кликните по вкладке Insert и затем, в разделе Code, выберите Task > Optimize.
Для использования во вводе проблемных данных вставьте новый раздел путем нажатия кнопки Section Break на вкладке Insert. Новые разделы появляются выше и ниже задачи.
В новом разделе выше задачи введите следующий код, чтобы задать начальную точку и целевую функцию.
x0 = [0 0]; fun = @dejong5fcn;
Чтобы поместить эти переменные в рабочую область, запустите раздел путем нажатия Ctrl+Enter.
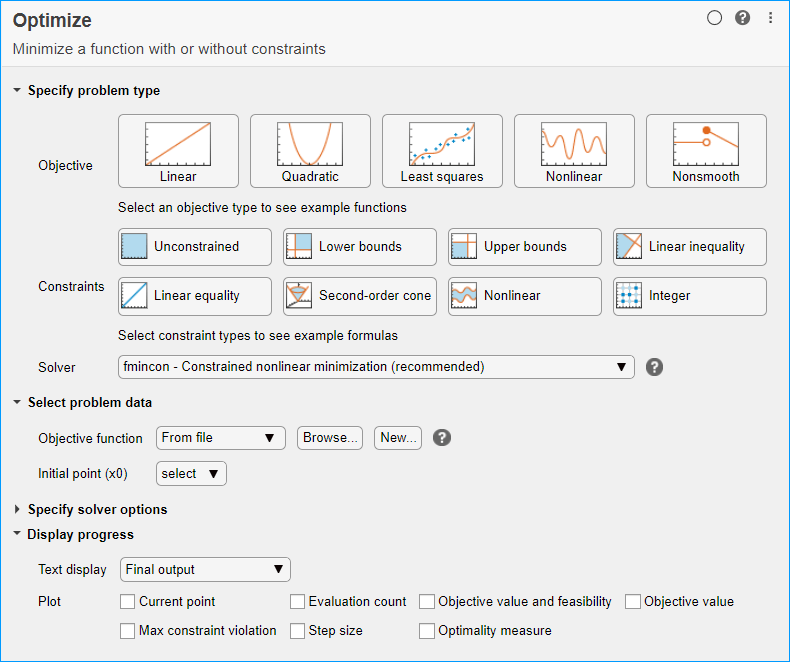
В разделе Specify problem type задачи нажмите кнопку Objective > Nonlinear.
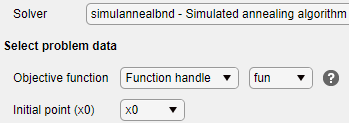
Выберите Solver > simulannealbnd - Simulated annealing algorithm.
В разделе Select problem data задачи выберите Objective function > Function handle и затем выберите fun.
Выберите Initial point (x0) > x0.
В разделе Display progress задачи выберите график Best value.
Чтобы запустить решатель, кликните по кнопке ⁝ опций в правом верхнем из окна задачи и выберите Run Section. График появляется в отдельном окне рисунка и в области вывода задачи. Обратите внимание на то, что ваш график может отличаться от один показанный, потому что simulannealbnd стохастический алгоритм.
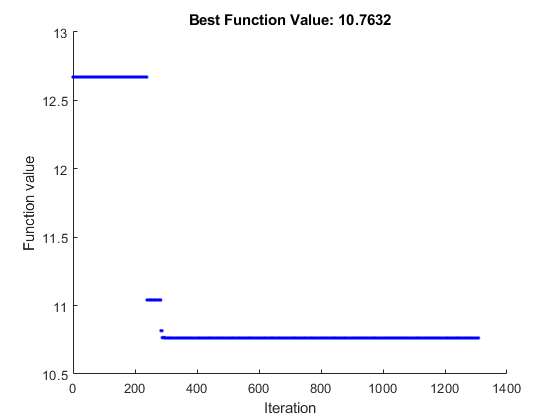
Чтобы видеть решение и лучшее значение целевой функции, посмотрите во главе задачи.
![]()
Оптимизировать задача Live Editor возвращает переменные под названием solution и objectiveValue к рабочей области.
Чтобы просмотреть значения эти переменные, введите следующий код в разделе ниже задачи.
disp(solution) disp(objectiveValue)
Запустите раздел путем нажатия Ctrl+Enter.
disp(solution)
-32.0285 -0.1280
disp(objectiveValue)
10.7632
И Оптимизировать задача Live Editor и командная строка позволяют вам формулировать и решать проблемы, и они дают идентичные результаты. Командная строка более оптимизирована, но обеспечивает меньше справки для выбора решателя, подготовки проблема и выбора опций, таких как функции построения графика. Можно также запустить, использование задач Оптимизируют, и затем генерируют код для использования командной строки, когда в Решают Ограниченную Нелинейную задачу, Основанную на решателе.