Смешанное Целое число ga Оптимизация

Смешанное целое число `ga` Оптимизация

Решение смешанных целочисленных задач оптимизации

ga может решить задачи, когда определенные переменные с целочисленным знаком. Дайте intcon, вектор из компонентов x, которые являются целыми числами:

[x,fval,exitflag] = ga(fitnessfcn,nvars,A,b,[],[],...
    lb,ub,nonlcon,intcon,options)

intcon вектор из положительных целых чисел, который содержит компоненты x, которые с целочисленным знаком. Например, если вы хотите ограничить x(2) и x(10) чтобы быть целыми числами, установите intcon к [2,10].

surrogateopt решатель также принимает целочисленные ограничения.

Примечание

Ограничения существуют на типах проблем это ga может решить с целочисленными переменными. В частности, ga не принимает нелинейные ограничения равенства, когда существуют целочисленные переменные. Для получения дополнительной информации смотрите Характеристики Целого числа ga Решатель.

Совет

ga решает целочисленные задачи лучше всего, когда вы обеспечиваете нижние и верхние границы для каждого компонента x.

Смешанная целочисленная оптимизация функции Рэстриджина

Скрипт Open Live Script

В этом примере показано, как найти минимум функции Рэстриджина ограниченным, таким образом, первый компонент x является целым числом. Компоненты x далее ограничиваются, чтобы быть в области $5 π \leq x (1) \leq 20 π, - 20 π \leq x (2) \leq - 4 π$ .

Настройте границы для своей проблемы

lb = [5*pi,-20*pi];
ub = [20*pi,-4*pi];

Установите функцию построения графика, таким образом, можно просмотреть прогресс ga

opts = optimoptions('ga','PlotFcn',@gaplotbestf);

Вызовите ga решатель, где x (1) имеет целочисленные значения

rng(1,'twister') % for reproducibility
intcon = 1;
[x,fval,exitflag] = ga(@rastriginsfcn,2,[],[],[],[],...
    lb,ub,[],intcon,opts)

Figure Genetic Algorithm contains an axes object. The axes object with title Best: 424.136 Mean: 614.506 contains 2 objects of type line. These objects represent Best penalty value, Mean penalty value.

Optimization terminated: average change in the penalty fitness value less than options.FunctionTolerance
and constraint violation is less than options.ConstraintTolerance.

x = 1×2

   16.0000  -12.9325

fval = 424.1355

exitflag = 1

ga сходится быстро к решению.

Характеристики Целого числа ga Решатель

Существуют некоторые ограничения на типы проблем это ga может решить, когда вы включаете целочисленные ограничения:

Никакие нелинейные ограничения равенства. Любая нелинейная ограничительная функция должна возвратить [] для нелинейного ограничения равенства. Для возможного обходного решения смотрите Пример: Целочисленное программирование с Нелинейным Ограничением равенства.
Только doubleVector тип населения.
Никакая гибридная функция. ga переопределения любая установка HybridFcn опция.
ga игнорирует ParetoFraction, DistanceMeasureFcn, InitialPenalty, и PenaltyFactor опции.

Перечисленные ограничения являются в основном естественными, не произвольными. Например, никакие гибридные функции не поддерживают целочисленные ограничения. Так ga не использует гибридные функции, когда существуют целочисленные ограничения.

Пример: целочисленное программирование с нелинейным ограничением равенства

Этот пример пытается определить местоположение минимума функции Ackley (включенный с вашим программным обеспечением) в пяти размерностях с этими ограничениями:

x(1), x(3), и x(5) целые числа.
norm(x) = 4.

Функция Ackley затрудняет, чтобы минимизировать. Добавление целочисленных и ограничений равенства увеличивает трудность.

Чтобы включать нелинейное ограничение равенства, дайте маленькому допуску tol это позволяет норму x быть в tol из 4. Без допуска никогда не удовлетворяют нелинейному ограничению равенства, и решатель не понимает, когда это имеет возможное решение.

Запишите выражению   norm(x) = 4 как два “меньше, чем нулевые” неравенства:
  norm(x) - 4≤ 0
  -(norm(x) - 4)≤ 0  . (1)
Позвольте маленький допуск в неравенствах:
norm(x) - 4 - tol≤ 0
-(norm(x) - 4) - tol≤ 0 . (2)
Запишите нелинейную функцию ограничения неравенства, которая реализует эти неравенства:
```
function [c, ceq] = eqCon(x)

ceq = [];
rad = 4;
tol = 1e-3;
confcnval = norm(x) - rad;
c = [confcnval - tol;-confcnval - tol];
```
Установка опций:
- MaxStallGenerations = 50 — Позвольте решателю пробовать некоторое время.
- FunctionTolerance = 1e-10 — Задайте более строгий критерий остановки чем обычно.
- MaxGenerations = 300 — Позвольте больше поколений, чем значение по умолчанию.
- PlotFcn = @gaplotbestfun — Наблюдайте оптимизацию.
```
opts = optimoptions('ga','MaxStallGenerations',50,'FunctionTolerance',1e-10,...
    'MaxGenerations',300,'PlotFcn',@gaplotbestfun);
```
Установите нижние и верхние границы помогать решателю:
```
nVar = 5;
lb = -5*ones(1,nVar);
ub = 5*ones(1,nVar);
```

Решите задачу:

rng(0,'twister') % for reproducibility
[x,fval,exitflag] = ga(@ackleyfcn,nVar,[],[],[],[], ...
    lb,ub,@eqCon,[1 3 5],opts);

Optimization terminated: average change in the penalty fitness value less than options.FunctionTolerance
and constraint violation is less than options.ConstraintTolerance.

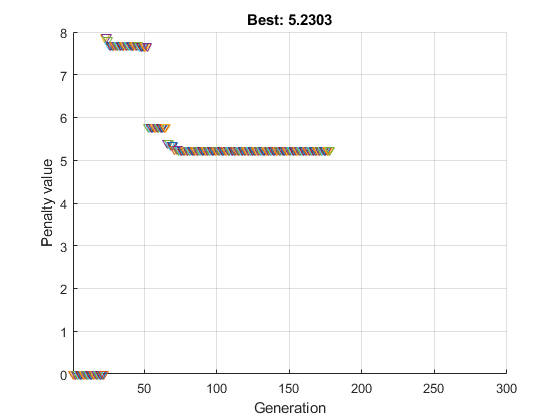
Исследуйте решение:
```
x,fval,exitflag,norm(x)

x =

         0   -1.7367   -3.0000   -0.0000   -2.0000


fval =

    5.2303


exitflag =

     1


ans =

    4.0020
```
Нечетный x компоненты являются целыми числами, как задано. Норма x 4, к в данной относительной погрешности 1e-3.
Несмотря на положительный выходной флаг, решение не является глобальным оптимумом. Запустите проблему снова и исследуйте решение:
```
opts = optimoptions('ga',opts,'Display','off');
[x2,fval2,exitflag2] = ga(@ackleyfcn,nVar,[],[],[],[], ...
    lb,ub,@eqCon,[1 3 5],opts);
```
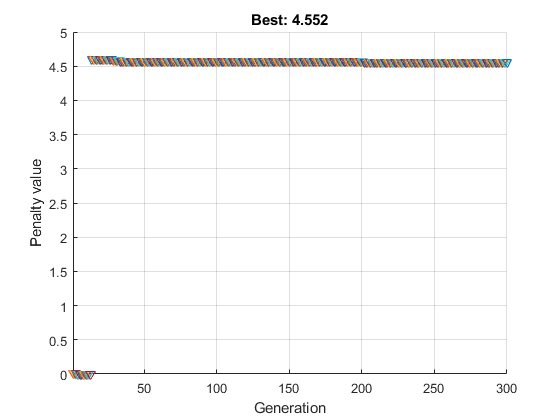
Исследуйте второе решение:
```
x2,fval2,exitflag2,norm(x2)
```
```
x2 =

   -2.0000    2.8930         0   -1.9095         0


fval2 =

    4.5520


exitflag2 =

     0


ans =

    4.0020
```
Второй запуск дает лучшее решение (более низкое значение функции фитнеса). Снова, нечетный x компоненты являются целыми числами и нормой x2 4, к в данной относительной погрешности 1e-3.

Следует иметь в виду, что эта процедура может перестать работать; ga испытывает трудности с одновременными целочисленными и ограничениями равенства.

Эффективное целое число `ga`

Использовать ga наиболее эффективно на целочисленных задачах, следуйте этим инструкциям.

Связанный каждый компонент так плотно, как вы можете. Эта практика дает ga самое маленькое пространство поиска, включая ga искать наиболее эффективно.
Если вы не можете, связал компонент, то укажите соответствующий начальный диапазон. По умолчанию, ga создает начальную генеральную совокупность с областью значений [-1e4,1e4] для каждого компонента. Меньшая или большая начальная область значений может дать лучшие результаты, когда значение по умолчанию является несоответствующим. Чтобы изменить начальную область значений, используйте InitialPopulationRange опция.
Если вы имеете больше чем 10 переменных, устанавливаете численность населения, которая больше, чем значение по умолчанию при помощи PopulationSize опция. Значение по умолчанию 200 для шести или больше переменных. Для размера значительной части населения:
- ga может занять много времени, чтобы сходиться. Если вы достигаете, максимальное количество поколений (выйдите из флага 0), увеличьте значение MaxGenerations опция.
- Уменьшите уровень мутации. Для этого увеличьте значение CrossoverFraction опция от ее значения по умолчанию 0.8 к 0.9 или выше.
- Увеличьте значение EliteCount опция от ее значения по умолчанию 0.05*PopulationSize к 0.1*PopulationSize или выше.

Для получения информации об опциях смотрите ga options входной параметр.

Целочисленный `ga` Алгоритм

Целочисленное программирование с ga включает несколько модификаций основного алгоритма (см. Как работы Генетического алгоритма). Для целочисленного программирования:

По умолчанию специальное создание, перекрестное соединение и функции мутации осуществляют переменные, чтобы быть целыми числами. Для получения дополнительной информации смотрите Глубоко и др. [2].
Если вы используете создание не по умолчанию, перекрестное соединение или функции мутации, ga осуществляет линейную выполнимость и выполнимость относительно целочисленных ограничений в каждой итерации.
Генетический алгоритм пытается минимизировать функцию штрафа, не функцию фитнеса. Функция штрафа включает термин для недопустимости. Эта функция штрафа объединена с бинарным выбором турнира по умолчанию, чтобы выбрать индивидуумов для последующих поколений. Значение функции штрафа члена населения:
- Если член выполним, функция штрафа является функцией фитнеса.
- Если член неосуществим, функция штрафа является максимальной функцией фитнеса среди выполнимых членов населения плюс сумма нарушений ограничений (неосуществимой) точки.
Для получения дополнительной информации функции штрафа, смотрите Деб [1].

Ссылки

[1] Деб, Kalyanmoy. Эффективный ограничительный метод обработки для генетических алгоритмов. Компьютерные Методы в Прикладной Механике и Разработке, 186 (2–4), стр 311–338, 2000.

[2] Глубоко, Kusum, Кришна Пратап Сингх, М.Л. Кэнсэл и К. Мохэн. Действительный закодированный генетический алгоритм для решения целого числа и смешанных целочисленных задач оптимизации. Прикладная математика и Расчет, 212 (2), стр 505–518, 2009.

Документация