Что такое многоцелевая оптимизация?

Вы можете должны быть сформулировать проблемы больше чем с одной целью, поскольку одна цель с несколькими ограничениями не может соответственно представлять стоявшую проблему. Если так, существует вектор из целей,

F (x) = [F ₁ (x), F ₂ (x)..., F _m (x)],

(1)

это должно быть обменяно в некотором роде. Относительная важность этих целей не является общеизвестной, пока лучшие возможности системы не определяются и компромиссы между целями, полностью изученными. Как количество увеличений целей, компромиссы, вероятно, станут комплексными и менее легко определенными количественно. Разработчик должен использовать его интуицию и способность описать настройки в цикле оптимизации. Таким образом требования для многоцелевой стратегии проектирования должны позволить естественной формулировке задачи быть описанной и смочь решить задачу и ввести настройки в численно послушную и реалистическую проблему проектирования.

Многоцелевая оптимизация касается минимизации вектора из целей F (x), который может быть предметом многих ограничений или границ:

$\begin{array}{l} \min_{x \in ℝ^{n}} F (x), при ограничениях \\ G_{i} (x) = 0, i = 1, ..., k_{e}; G_{i} (x) \leq 0, i = k_{e} + 1, ..., k; l \leq x \leq u . \end{array}$

Обратите внимание на то, что, потому что F (x) является вектором, если какой-либо из компонентов F (x) конкурирует, нет никакого уникального решения этой проблемы. Вместо этого концепция ненеполноценности в Zadeh [4] (также названный оптимальностью Парето в Цензоре [1] и Da Cunha и Полак [2]) должна использоваться, чтобы охарактеризовать цели. Ненижнее решение - то, в котором улучшение одной цели требует ухудшения другого. Чтобы задать эту концепцию более точно, рассмотрите выполнимую область, Ω, в пространстве параметров. x является элементом n - размерные вещественные числа $x \in ℝ^{n}$ это удовлетворяет всем ограничениям, то есть,

$Ω = {x \in ℝ^{n}},$

при ограничениях

$\begin{array}{l} G_{i} (x) = 0, i = 1, ..., k_{e}, \\ G_{i} (x) \leq 0, i = k_{e} + 1, ..., k, \\ l \leq x \leq u . \end{array}$

Это позволяет определение соответствующей выполнимой области для пробела целевой функции Λ:

$Λ = {y \in ℝ^{m} : y = F (x), x \in Ω} .$

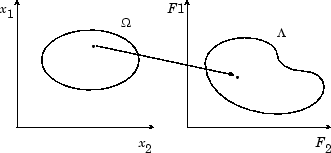
Вектор эффективности F (x) пространство параметров карт в пробел целевой функции, как представлено в двух измерениях в рисунке 13-1 фигуры, Сопоставляющем от Пространства параметров в Пробел Целевой функции.

Рисунок 13-1, сопоставляющий от пространства параметров в пробел целевой функции

Ненижняя точка решения может теперь быть задана.

Определение: точка $x * \in Ω$ ненижнее решение, если для некоторого окружения x* там не существует Δx, таким образом что $(x * + Δ x) \in Ω$ и

$\begin{array}{l} F_{i} (x * + Δ x) \leq F_{i} (x *), i = 1, ..., m, и \\ F_{j} (x * + Δ x) < F_{j} (x *) для по крайней мере одного j . \end{array}$

В двумерном представлении рисунка 13-2 фигуры, Наборе Ненижних Решений, набор ненижних решений находится на кривой между C и D. Точки A и B представляют определенные ненижние точки.

Рисунок 13-2, набор ненижних решений

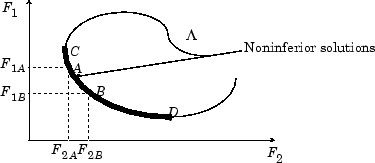
A и B являются явно ненижними точками решения, потому что улучшение одной цели, F ₁, требует ухудшения в другой цели, F ₂, то есть, F _1B < F _1A, F _2B > F _2A.

Поскольку любая точка в Ω, который является нижней точкой, представляет точку, в которой улучшение может быть достигнуто во всех целях, ясно, что такая точка не представляет ценности. Многоцелевая оптимизация, поэтому, касается генерации и выбора ненижних точек решения.

Ненижние решения также называются Pareto optima. Общая цель в многоцелевой оптимизации создает optima Парето.

Документация Global Optimization Toolbox

Поддержка

Памятка переводчика

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Документация