Ядра от рассеяния - собирают операции типа

GPU Coder™ также поддерживает концепцию сокращений - важное исключение к правилу, что итерации цикла должны быть независимыми. Переменная сокращения накапливает значение, которое зависит от всех итераций вместе, но независимо от порядка итерации. Переменные сокращения появляются и на стороне оператора присваивания, такой как в суммировании, скалярном произведении, и на виде. Следующий пример показывает типичное использование переменной x сокращения:

x = ...; % Some initialization of x
for i = 1:n
  x = x + d(i);
end

Переменная x в каждой итерации получает ее значение или прежде, чем ввести цикл или от предыдущей итерации цикла. Эта последовательная реализация типа порядка не подходит для параллельного выполнения из-за цепи зависимостей в последовательном выполнении. Альтернативный подход должен использовать основанный на двоичном дереве подход.

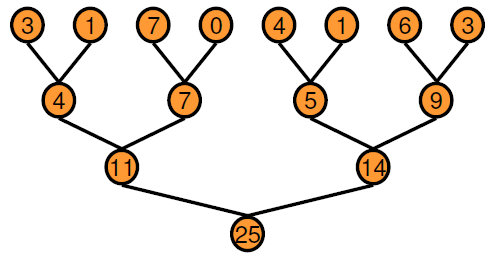
В основанном на дереве подходе можно выполнить каждый горизонтальный уровень дерева параллельно по определенному числу передач. Когда по сравнению с последовательным выполнением, двоичное дерево действительно требует большей памяти, потому что каждая передача требует массива временных ценностей, как выведено. Выигрыш в производительности, который вы получаете далеко, перевешивает стоимость увеличенного использования памяти. GPU Coder создает ядра сокращения при помощи этого основанного на дереве подхода, где каждый блок потока уменьшает фрагмент массива. Параллельное сокращение требует частичных обменов данными результата между блоками потока. В более старом CUDA^® устройства, этот обмен данными был достигнут при помощи синхронизации потока и общей памяти. Начиная с архитектуры графического процессора Кеплера CUDA обеспечивает перестановку (shfl) инструкция и быстрая память устройства атомарные операции, которые делают сокращения еще быстрее. Ядра сокращения, которые создает GPU Coder, используют shfl_down инструкция уменьшать через деформацию (32 потока) потоков. Затем первый поток каждой деформации использует атомарные инструкции по операции обновить уменьшаемое значение.

Для получения дополнительной информации об инструкциях обратитесь к NVIDIA^® документация.

Векторный пример суммы

В этом примере показано, как создать ядра типа сокращения CUDA при помощи GPU Coder. Предположим, что вы хотите создать векторный v и вычислите сумму его элементов. Можно реализовать этот пример как MATLAB^® функция.

function s = VecSum(v)
    s = 0;
    for i = 1:length(v)
       s = s + v(i);
    end
end

Подготовьте vecSum к Созданию Ядра

GPU Coder требует, чтобы никакая специальная прагма не вывела ядра сокращения. В этом примере используйте coder.gpu.kernelfun прагма, чтобы сгенерировать ядра сокращения CUDA. Используйте модифицированный VecSum функция.

function s = VecSum(v) %#codegen
    s = 0;
    
    coder.gpu.kernelfun();
    for i = 1:length(v)
       s = s + v(i);
    end
end

Сгенерированный код CUDA

Когда вы генерируете код CUDA при помощи приложения GPU Coder или из командной строки, GPU Coder создает одно ядро, которое выполняет векторное вычисление суммы. Следующее является отрывком vecSum_kernel1.

static __global__ __launch_bounds__(512, 1) void vecSum_kernel1(const real_T *v,
  real_T *s)
{
  uint32_T threadId;
  uint32_T threadStride;
  uint32_T thdBlkId;
  uint32_T idx;
  real_T tmpRed;
  ;
  ;
  thdBlkId = (threadIdx.z * blockDim.x * blockDim.y + threadIdx.y * blockDim.x)
    + threadIdx.x;
  threadId = ((gridDim.x * gridDim.y * blockIdx.z + gridDim.x * blockIdx.y) +
              blockIdx.x) * (blockDim.x * blockDim.y * blockDim.z) + thdBlkId;
  threadStride = gridDim.x * blockDim.x * (gridDim.y * blockDim.y) * (gridDim.z *
    blockDim.z);
  if (!((int32_T)threadId >= 512)) {
    tmpRed = 0.0;
    for (idx = threadId; threadStride < 0U ? idx >= 511U : idx <= 511U; idx +=
         threadStride) {
      tmpRed += v[idx];
    }

    tmpRed = workGroupReduction1(tmpRed, 0.0);
    if (thdBlkId == 0U) {
      atomicOp1(s, tmpRed);
    }
  }
}

Прежде, чем вызвать VecSum_kernel1, два cudaMemcpy вызовы передают векторный v и скалярный s с хоста на устройство. Ядро имеет один блок потока, содержащий 512 потоков на блок, сопоставимый с размером входного вектора. Треть cudaMemcpy вызовите копирует результат расчета назад к хосту. Следующее является отрывком основной функции.

  cudaMemcpy((void *)gpu_v, (void *)v, 4096ULL, cudaMemcpyHostToDevice);
  cudaMemcpy((void *)gpu_s, (void *)&s, 8ULL, cudaMemcpyHostToDevice);
  VecSum_kernel1<<<dim3(1U, 1U, 1U), dim3(512U, 1U, 1U)>>>(gpu_v, gpu_s);
  cudaMemcpy(&s, gpu_s, 8U, cudaMemcpyDeviceToHost);

Примечание

Для лучшей эффективности GPU Coder уделяет первостепенное значение, чтобы быть параллельным ядрам по сокращениям. Если ваш алгоритм содержит сокращение в параллельном цикле, GPU Coder выводит сокращение как регулярный цикл и генерирует ядра для него.

1D операции сокращения на графическом процессоре

Можно использовать gpucoder.reduce функция, чтобы сгенерировать код CUDA, который выполняет эффективные 1D операции сокращения на графическом процессоре. Сгенерированный код использует внутренние параметры перестановки CUDA, чтобы реализовать операцию сокращения.

Например, чтобы найти sum и max элементы массива A:

function s = myReduce(A)
   s = gpucoder.reduce(A, {@mysum, @mymax}); 
end

function c = mysum(a, b)
   c = a+b;
end

function c = mymax(a, b)
   c = max(a,b);
end

Для генерации кода, gpucoder.reduce функция имеет эти требования:

Вход должен иметь тип числовых данных или логический тип данных.
Функция прошла через @handle, должна быть двоичная функция, которая принимает два входных параметров и возвращает один выходной параметр. Вводы и выводы должны иметь совпадающий тип данных.
Функция должна быть коммутативной и ассоциативной.

Примечание

Для некоторых входных параметров, которые имеют целочисленный тип данных, код, сгенерированный для gpucoder.reduce функция может содержать промежуточные расчеты, которые достигают насыщения. В таких случаях результаты сгенерированного кода не могут совпадать с результатами симуляции из MATLAB.

Документация