Алгоритм Локализации Монте-Карло (MCL) используется, чтобы оценить положение и ориентацию робота. Алгоритм использует известную карту среды, данных о датчике области значений и данных датчика одометрии. Чтобы видеть, как создать объект и использовать этот алгоритм, смотрите monteCarloLocalization.
Чтобы локализовать робота, алгоритм MCL использует фильтр частиц, чтобы оценить его положение. Частицы представляют распределение вероятных состояний для робота. Каждая частица представляет возможное состояние робота. Частицы сходятся вокруг одного местоположения, когда робот перемещается в среду и обнаруживает различные части среды с помощью датчика области значений. Движение робота обнаруживается с помощью датчика одометрии.
Частицы обновляются в этом процессе:
Частицы распространены на основе изменения в положении и заданной модели движения, MotionModel.
Частицы являются присвоенными весами на основе вероятности получения датчика области значений, читающего для каждой частицы. Это чтение основано на модели датчика, которую вы задаете в SensorModel.
На основе этих весов оценка состояния робота извлечена на основе весов частицы. Группа частиц с самым высоким весом используется, чтобы оценить положение робота.
Наконец, частицы передискретизируются на основе заданного ResamplingInterval. Передискретизация регулирует положения частицы и улучшает производительность путем корректировки количества используемых частиц. Это - ключевая возможность для корректировки к изменениям и хранения частиц, важных для оценки состояния робота.
Алгоритм выводит предполагаемое положение и ковариацию. Эти оценки являются средним значением и ковариацией самого высокого взвешенного кластера частиц. Для непрерывного отслеживания повторите эти шаги в цикле, чтобы распространить частицы, оценить их вероятность и получить лучшую оценку состояния.
Для получения дополнительной информации о фильтрах частиц как общее применение смотрите Рабочий процесс Фильтра частиц.
При работе с алгоритмом локализации цель состоит в том, чтобы оценить состояние системы. Для приложений робототехники это предполагаемое состояние обычно является положением робота. Для monteCarloLocalization объект, вы указываете, что это изображает из себя трехэлементный вектор. Положение соответствует положению x-y, [x y], и угловая ориентация, theta.
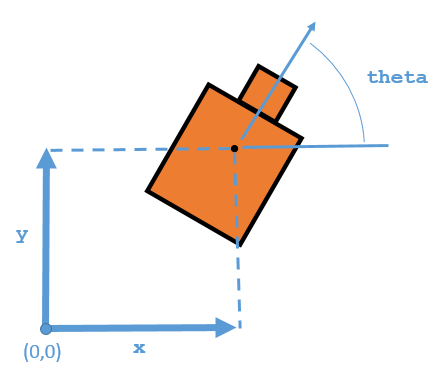
Алгоритм MCL оценивает эти три значения на основе входных параметров датчика среды и данной модели движения вашей системы. Выход от использования monteCarloLocalization объект включает pose, который является лучшим предполагаемым состоянием [x y theta] значения. Частицы распределяются вокруг начального положения, InitialPose, или произведенная однородно использующая глобальная локализация. Положение вычисляется как среднее значение самого высокого взвешенного кластера частиц, если эти частицы были откорректированы на основе измерений.
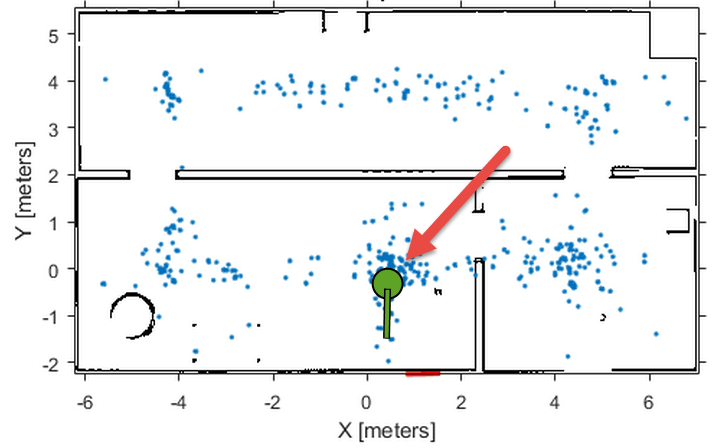
Этот график показывает самый высокий взвешенный кластер и итоговое положение робота, отображенное по демонстрационным частицам зеленого цвета. С большим количеством итераций алгоритма MCL и коррекций измерения, частицы сходятся к истинному местоположению робота. Однако возможно, что кластеры частицы могут иметь высокие веса для ложных оценок и сходиться на неправильном местоположении. Если неправильная сходимость происходит, передискретизируйте частицы путем сброса алгоритма MCL с обновленным InitialPose.
Когда вы сначала создаете monteCarloLocalization алгоритм, задайте минимальные и максимальные пределы частицы при помощи ParticleLimits свойство. Более высокое количество частиц увеличивает вероятность, что частицы сходятся на фактическом местоположении. Однако более низкий номер частицы быстрее. Количество частиц настраивает динамически в пределах на основе весов кластеров частицы. Эта корректировка помогает сократить количество частиц в зависимости от времени, таким образом, локализация может запуститься более эффективно.
Частицы должны быть произведены через заданное распределение. Чтобы инициализировать частицы в пространстве состояний, можно использовать или начальное положение или глобальную локализацию. С глобальной локализацией можно однородно распределить частицы на ожидаемом пространстве состояний (вытянутый от Map свойство yourSensorModel объект. В объекте MCL по умолчанию, набор GlobalLocalization свойство к true.
mcl = monteCarloLocalization; mcl.GlobalLocalization = true;
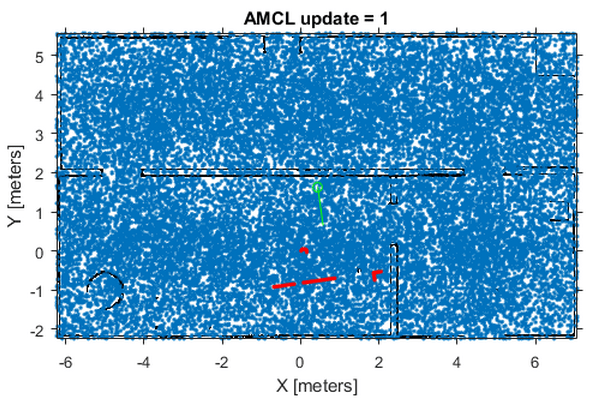
Глобальная локализация требует большего числа частиц к эффективно демонстрационным частицам через пространство состояний. Больше частиц увеличивает вероятность успешной сходимости на реальном положении. Это большое распределение значительно уменьшает начальную эффективность, пока частицы не начинают сходиться, и количество частицы может быть сокращено.
По умолчанию глобальная локализация установлена в false. Без глобальной локализации необходимо задать InitialPose и InitialCovariance свойства, который помогает локализовать частицы. Используя это начальное положение, частицы более тесно сгруппированы вокруг предполагаемого состояния. Близкая группировка частиц позволяет вам использовать меньше из них и увеличивает скорость и точность отслеживания во время первых итераций.
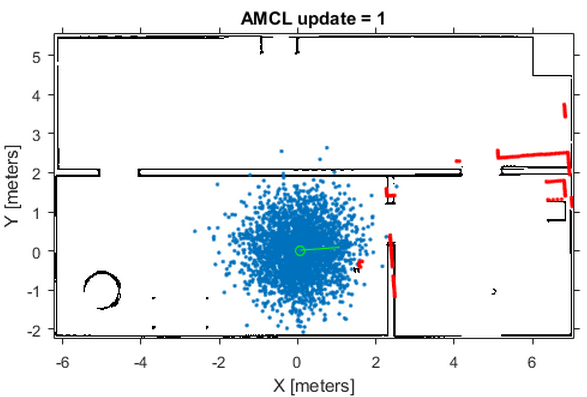
Эти изображения были взяты из Локализовать TurtleBot Используя пример Локализации Монте-Карло, который показывает, как использовать алгоритм MCL с TurtleBot® в известной среде.
Чтобы локализовать вашего робота постоянно, необходимо передискретизировать частицы и обновить алгоритм. Используйте UpdateThreshold и ResamplingInterval свойства управлять при передискретизации и обновления предполагаемого состояния происходят.
UpdateThreshold трехэлементный вектор, который задает минимальное изменение в положении робота, [x y theta], инициировать обновление. Замена переменной больше, чем этим минимумом инициировала обновление, вызывая объект возвратить новую оценку состояния. Это изменение в положении робота основано на одометрии, которая задана в функциональной форме объекта. Настройте эти пороги на основе своих свойств датчика и движения вашего робота. Случайные шумовые или незначительные изменения, больше, чем ваш порог, могут инициировать ненужное обновление и влиять на вашу эффективность. ResamplingInterval свойство задает количество обновлений, чтобы инициировать передискретизацию частицы. Например, интервал передискретизации 2 передискретизирует при любом обновлении.
Преимущество передискретизации частиц - то, что вы обновляете возможные местоположения, которые способствуют итоговой оценке. Передискретизация перераспределяет частицы на основе их весов и развивает частицы на основе Модели Движения. В этом процессе частицы с более низким весом устраняются, помогая частицам сходиться к истинному состоянию робота. Количество частиц динамически изменяется, чтобы улучшить скорость или отслеживание.
Эффективность алгоритма зависит от соответствующей передискретизации. Если частицы широко рассеиваются, и начальное положение робота не известно, алгоритм обеспечивает высокое количество частицы. Когда алгоритм сходится на истинном местоположении, он сокращает количество частиц и увеличивает скорость эффективности. Можно настроить ParticleLimits свойство ограничить минимальные и максимальные частицы раньше помогало с эффективностью.
Движение и модели датчика для алгоритма MCL похожи на StateTransitionFcn и MeasurementLikelihoodFcn функции для stateEstimatorPF объект, которые описаны в Параметрах Фильтра частиц. Для алгоритма MCL эти модели более характерны для локализации робота. После вызова объекта, чтобы изменить MotionModel или SensorModel свойства, необходимо сначала вызвать release на вашем объекте.
По умолчанию, monteCarloLocalization использует likelihoodFieldSensorModel возразите как модель датчика. Эта модель датчика содержит параметры, характерные для датчика области значений используемая, 2D информация о карте для среды робота и характеристики шума измерения. Модель датчика использует параметры с измерениями области значений, чтобы вычислить вероятность измерений, учитывая текущее положение робота. Без включающего эти параметры некоторые погрешности измерения могут скосить оценку состояния или увеличить вес на несоответствующих частицах.
Свойства датчика области значений:
SensorPose – Положение датчика области значений относительно местоположения робота. Это положение используется, чтобы преобразовать показания области значений в систему координат координаты робота.
SensorLimits – Минимум и максимум располагаются пределы. Измерение за пределами этих областей значений не включено в вычисление вероятности.
NumBeams – Количество лучей раньше вычисляло вероятность. Можно улучшить скорость эффективности путем сокращения количества используемых лучей.
Измерения области значений, как также известно, дают ложные показания из-за системного шума или другой экологической интерференции. С учетом ошибки датчика задайте эти параметры:
MeasurementNoise – Стандартное отклонение для шума измерения. Это отклонение применяется к чтению области значений и составляет любую интерференцию с датчиком. Установите это значение на основе информации от вашего датчика области значений.
RandomMeasurementWeight — Вес для вероятности случайного измерения. Установите низкую вероятность для случайных измерений. Значение по умолчанию 0.05.
ExpectedMeasurementWeight — Вес для вероятности ожидаемого измерения. Установите высокую вероятность для ожидаемых измерений. Значение по умолчанию 0.95.
Модель датчика также хранит карту среды робота как сетка заполнения. Используйте binaryOccupancyMap задавать вашу карту с занятыми и свободными пространствами. Установите любые неизвестные пробелы в карте как свободные местоположения. Установка их к свободным местоположениям препятствует тому, чтобы алгоритм совпадал с обнаруженными объектами к этим областям карты.
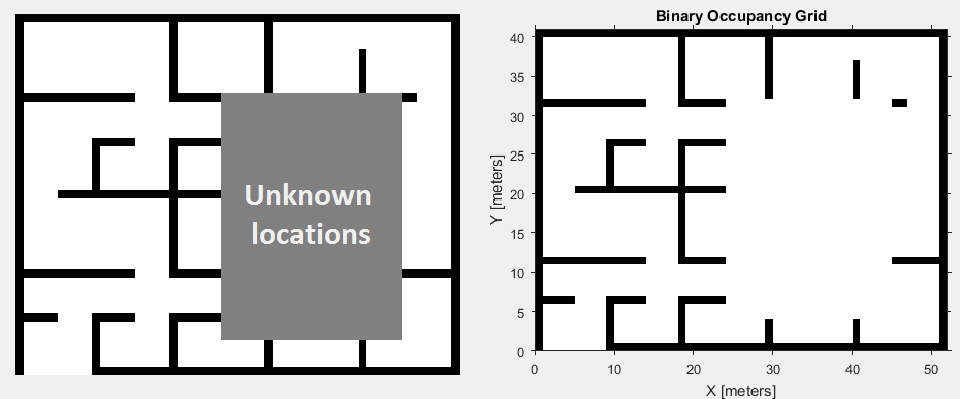
Кроме того, можно задать MaximumLikelihoodDistance, который ограничивает область для поиска препятствий. Значение MaximumLikelihoodDistance максимальное расстояние до самого близкого препятствия, которое используется для расчета вероятности.
Модель движения для локализации робота помогает предсказать, как частицы развиваются в течение времени при передискретизации. Это - представление кинематики робота. Модель движения, включенная по умолчанию с алгоритмом MCL, является основанной на одометрии дифференциальной моделью движения диска (odometryMotionModel). Без модели движения, предсказывая следующий шаг больше затрудняет. Важно знать возможности вашей системы так, чтобы алгоритм локализации мог запланировать распределения частицы, чтобы получить лучшие оценки состояния. Обязательно рассмотрите ошибки от энкодеров колеса, или другие датчики раньше измеряли одометрию. Ошибки в системе задают распространение распределения частицы.
Можно задать ошибку, ожидаемую на основе движения робота как четырехэлементный вектор, Noise. Эти четыре элемента указаны как веса на стандартных отклонениях для [1]:
Вращательная ошибка из-за вращательного движения
Вращательная ошибка из-за поступательного движения
Поступательная ошибка из-за поступательного движения
Поступательная ошибка из-за вращательного движения
Для роботов с дифференциальным приводом, когда робот перемещается от стартового положения до итогового положения, изменение в положении может быть обработано как:
Вращение к конечному положению
Перевод в прямой линии к конечному положению
Вращение к целевой ориентации
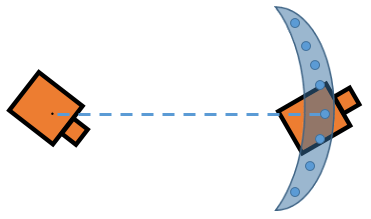
Принимая эти шаги, можно визуализировать эффект ошибок попеременно и перевода. Ошибки в начальном вращении приводят к вашим возможным положениям, распространяемым в C-форме вокруг конечного положения.
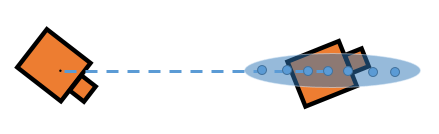
Большие поступательные ошибки приводят к вашим возможным положениям, распространяемым вокруг прямой линии к конечному положению.
Большие ошибки и в переводе и во вращении могут привести к шире распространенным положениям.
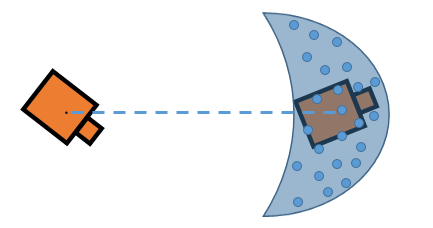
Кроме того, вращательные ошибки влияют на ориентацию итогового положения. Понимание этих эффектов помогает вам задать Гауссов шум в Noise свойство MotionModel возразите для своего определенного приложения. Когда изображения показывают, каждый параметр непосредственно не управляет дисперсией и может меняться в зависимости от вашей настройки робота и геометрии. Кроме того, несколько изменений положения как робот перешли через вашу среду, может увеличить эффекты этих ошибок по многим различным шагам. Путем точного определения этих параметров частицы распределяются соответственно, чтобы дать алгоритму MCL достаточно гипотез, чтобы найти наилучшую оценку для местоположения робота.
[1] Трун, Себастьян и Дитер Фокс. Вероятностная Робототехника. 3-й редактор Кембридж, Масса: Нажатие MIT, 2006. p.136.
monteCarloLocalization | likelihoodFieldSensorModel | odometryMotionModel