Автоматическое дифференцирование (также известный как autodiff, AD или algorithmic differentiation) является широко используемым инструментом в оптимизации. solve функционируйте использует автоматическое дифференцирование по умолчанию в основанной на проблеме оптимизации для общих нелинейных целевых функций и ограничениях; смотрите Автоматическое Дифференцирование в Optimization Toolbox.
Автоматическое дифференцирование является набором методов для оценки производных (градиенты) численно. Метод использует символьные правила для дифференцирования, которые более точны, чем приближения конечной разности. В отличие от чисто символьного подхода, автоматическое дифференцирование выполняет выражения численно рано в расчетах, вместо того, чтобы выполнить большие символьные расчеты. Другими словами, автоматическое дифференцирование оценивает производные в конкретных числовых значениях; это не создает символьные выражения для производных.
Forward mode автоматическое дифференцирование оценивает числовую производную путем выполнения элементарных производных операций одновременно с операциями выполнения самой функции. Как детализировано в следующем разделе, программное обеспечение выполняет эти расчеты на вычислительном графике.
Reverse mode автоматическое дифференцирование использует расширение прямого режима вычислительный график, чтобы включить расчет градиента противоположным обходом графика. Когда программное обеспечение запускает код, чтобы вычислить функцию и ее производную, это записывает операции в структуре данных, названной trace.
Как многие исследователи отметили (например, Baydin, Pearlmutter, Радул и Siskind [1]), для скалярной функции многих переменных, реверсный режим вычисляет градиент более эффективно, чем прямой режим. Поскольку целевая функция является скаляром, solve автоматическое дифференцирование использует реверсный режим для скалярной оптимизации. Однако для функций с векторным знаком, таких как нелинейный метод наименьших квадратов и решение уравнения, solve использование передает режим для некоторых вычислений. Смотрите Автоматическое Дифференцирование в Optimization Toolbox.
Рассмотрите задачу выполнения этой функции и ее градиента:
Автоматическое дифференцирование работает в конкретных точках. В этом случае возьмите x 1 = 2, x 2 = 1/2.
Следующий вычислительный график кодирует вычисление функционального f (x).
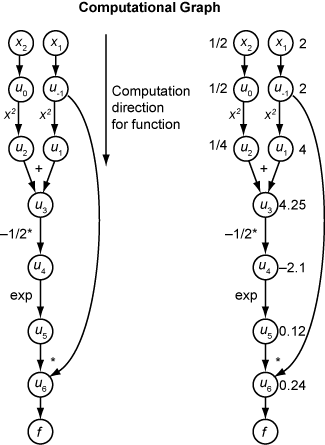
Чтобы вычислить градиент f (x) с помощью прямого режима, вы вычисляете тот же график в том же направлении, но изменяете расчет на основе элементарных правил дифференцирования. Чтобы далее упростить вычисление, вы заполняете значение производной каждого подвыражения ui, когда вы идете. Чтобы вычислить целый градиент, необходимо пересечь график дважды, однажды для частной производной относительно каждой независимой переменной. Каждое подвыражение в цепочечном правиле имеет числовое значение, таким образом, целое выражение имеет тот же вид графика оценки как сама функция.
Расчет является повторным приложением цепочечного правила. В этом примере производная f относительно x 1 расширяется до этого выражения:
Пусть представляйте производную выражения ui относительно x 1. Используя оцененные значения ui от вычисления функции, вы вычисляете частную производную f относительно x 1 как показано в следующем рисунке. Заметьте, что все значения станьте доступными, когда вы пересекаете график сверху донизу.
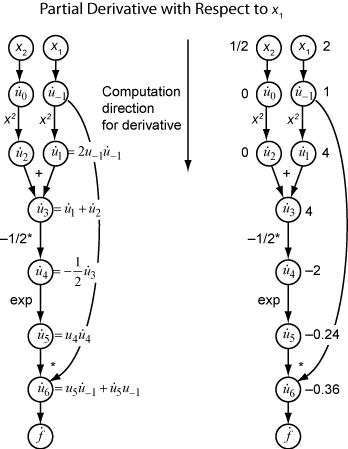
Чтобы вычислить частную производную относительно x 2, вы пересекаете подобный вычислительный график. Поэтому, когда вы вычисляете градиент функции, количество обходов графика совпадает с количеством переменных. Этот процесс может быть медленным для многих приложений, когда целевая функция или нелинейные ограничения зависят от многих переменных.
Реверсный режим использует один прямой обход вычислительного графика, чтобы настроить трассировку. Затем это вычисляет целый градиент функции в одном обходе графика в противоположном направлении. Для проблем со многими переменными этот режим намного более эффективен.
Теория позади реверсного режима также основана на цепочечном правиле, наряду со связанными примыкающими переменными, обозначенными со сверхпанелью. Примыкающая переменная для ui
В терминах вычислительного графика каждая исходящая стрела из переменной способствует соответствующей примыкающей переменной своим термином в цепочечном правиле. Например, переменная u –1 имеет исходящие стрелы к двум переменным, u 1 и u 6. График имеет связанное уравнение
В этом вычислении, вспоминая это и u 6 = u 5u–1, вы получаете
Во время прямого обхода графика программное обеспечение вычисляет промежуточные переменные ui. Во время противоположного обхода, начинающего с начального значения , расчет реверсного режима получает примыкающие значения для всех переменных. Поэтому реверсный режим вычисляет градиент во всего одном расчете, экономя много времени, сравненного с прямым режимом.
Следующий рисунок показывает расчет градиента в реверсном режиме для функции
Снова, расчет берет x 1 = 2, x 2 = 1/2. Расчет реверсного режима использует значения ui, которые получены во время расчета функции в исходном вычислительном графике. В правильном фрагменте фигуры вычисленные значения примыкающих переменных появляются рядом с примыкающими именами переменных, с помощью формул от левого фрагмента фигуры.
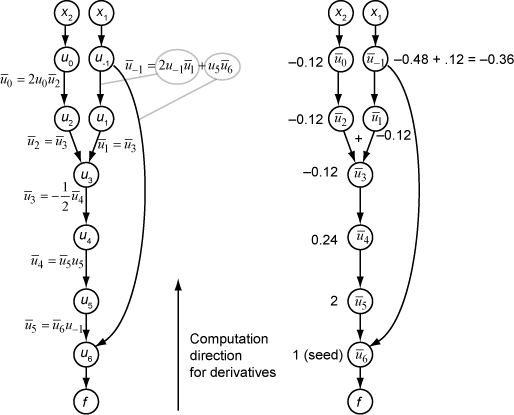
Итоговые значения градиента появляются как и .
Для получения дополнительной информации смотрите Baydin, Pearlmutter, Радул, и Siskind [1] или статью Wikipedia об автоматическом дифференцировании [2].
Автоматическое дифференцирование (AD) применяется solve и prob2struct функции при следующих условиях:
Цель и ограничительные функции поддерживаются, как описано в Поддерживаемых Операциях для Переменных и выражений Оптимизации. Они не требуют использования fcn2optimexpr функция.
Решатель, вызванный solve fmincon, fminunc, fsolve, или lsqnonlin.
Для задач оптимизации, 'ObjectiveDerivative' и 'ConstraintDerivative' аргументы пары "имя-значение" для solve или prob2struct установлены в 'auto' (значение по умолчанию), 'auto-forward', или 'auto-reverse'.
Для проблем уравнения, 'EquationDerivative' опция установлена в 'auto' (значение по умолчанию), 'auto-forward', или 'auto-reverse'.
| Когда AD применяется | Все ограничительные поддерживаемые функции | Одно или несколько ограничений, не поддержанных |
|---|---|---|
| Поддерживаемая целевая функция | AD используется для цели и ограничений | AD, используемый для цели только |
| Целевая функция, не поддерживаемая | AD, используемый для ограничений только | AD, не используемый |
Когда этим условиям не удовлетворяют, solve оценочные градиенты конечными разностями, и prob2struct не создает градиенты в его сгенерированных файлах функции.
Решатели выбирают следующий тип AD по умолчанию:
Для общей нелинейной целевой функции, fmincon значения по умолчанию, чтобы инвертировать AD для целевой функции. fmincon значения по умолчанию, чтобы инвертировать AD для нелинейного ограничения функционируют, когда количество нелинейных ограничений меньше количества переменных. В противном случае, fmincon значения по умолчанию, чтобы передать AD для нелинейной ограничительной функции.
Для общей нелинейной целевой функции, fminunc значения по умолчанию, чтобы инвертировать AD.
Для целевой функции наименьших квадратов, fmincon и fminunc значение по умолчанию, чтобы передать AD для целевой функции. Для определения основанной на проблеме целевой функции наименьших квадратов смотрите Целевую функцию Записи для Основанных на проблеме Наименьших квадратов.
lsqnonlin значения по умолчанию, чтобы передать AD, когда число элементов в объективном векторе больше или равно количеству переменных. В противном случае, lsqnonlin значения по умолчанию, чтобы инвертировать AD.
fsolve значения по умолчанию, чтобы передать AD, когда количество уравнений больше или равно количеству переменных. В противном случае, fsolve значения по умолчанию, чтобы инвертировать AD.
Примечание
Использовать автоматические производные в проблеме, преобразованной prob2struct, передайте опции, задающие эти производные.
options = optimoptions('fmincon','SpecifyObjectiveGradient',true,... 'SpecifyConstraintGradient',true); problem.options = options;
В настоящее время AD работает только на первые производные; это не применяется к вторым или производным высшего порядка. Так, например, если вы хотите использовать аналитический Гессиан, чтобы ускорить вашу оптимизацию, вы не можете использовать solve непосредственно, и должен вместо этого использовать подход, описанный в Производных Предоставления в Основанном на проблеме Рабочем процессе.
[1] Baydin, Atilim Gunes, Барак А. Перлматтер, Радул Алексея Андреевича и Джеффри Марк Сискинд. "Автоматическое Дифференцирование в Машинном обучении: Обзор". Журнал Исследования Машинного обучения, 18 (153), 2018, стр 1–43. Доступный в https://arxiv.org/abs/1502.05767.
[2] Автоматическое дифференцирование. Википедия. Доступный в https://en.wikipedia.org/wiki/Automatic_differentiation.