fminsearch Алгоритмfminsearch использует алгоритм симплекса Nelder-меда как описано в Lagarias и др. [57]. Этот алгоритм использует симплекс n + 1 точка для n - размерные векторы x. Алгоритм сначала делает симплекс вокруг исходного предположения x 0 путем добавления 5% каждого x компонента 0 (i) к x 0 и использования этих векторов n в качестве элементов симплекса в дополнение к x 0. (Алгоритм использует 0.00025 в качестве i компонента если x 0 (i) = 0.) Затем алгоритм неоднократно изменяет симплекс согласно следующей процедуре.
Примечание
Ключевые слова для fminsearch итеративное отображение появляется полужирным после описания шага.
Позволенный x (i) обозначают список точек в текущем симплексе, i = 1..., n + 1.
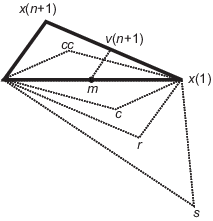
Закажите точки в симплексе от самого низкого значения функции f (x (1)) к самому высокому f (x (n + 1)). На каждом шаге в итерации алгоритм отбрасывает текущую худшую точку x (n + 1) и принимает другую точку в симплекс. [Или, в случае шага 7 ниже, это изменяет все точки n со значениями выше f (x (1))].
Сгенерируйте точку reflected
r = 2m – x (n + 1),
где
m = Σx (i)/n, i = 1... n,
и вычислите f (r).
Если f (x (1)) ≤ f (r) <f (x (n)), примите r и отключите эту итерацию. Отразиться
Если f (r) <f (x (1)), вычислите, расширение указывают s
s = m + 2 (m – x (n + 1)),
и вычислите f (s).
Если f (s) <f (r), примите s и отключите итерацию. Расширение
В противном случае примите r и отключите итерацию. Отразиться
Если f (r) ≥ f (x (n)), выполните contraction между m и eitherx (n + 1) или r, в зависимости от которого имеет более низкое значение целевой функции.
Если f (r) <f (x (n + 1)) (то есть, r лучше, чем x (n + 1)), вычислить
c = m + (r – m)/2
и вычислите f (c). Если f (c) < f (r), примите c и отключите итерацию. Контракт снаружи
В противном случае продолжите Шаг 7 (Уменьшение).
Если f (r) ≥ f (x (n + 1)), вычислить
cc = m + (x (n + 1) – m)/2
и вычислите f (cc). Если f (cc) < f (x (n + 1)), примите cc и отключите итерацию. Контракт внутри
В противном случае продолжите Шаг 7 (Уменьшение).
Вычислите точки n
v (i) = x (1) + (x (i) – x (1))/2
и вычислите f (v (i)), i = 2..., n + 1. Симплексом в следующей итерации является x (1), v (2)..., v (n + 1). Уменьшение
Следующий рисунок показывает точки это fminsearch может вычислить в процедуре, наряду с каждым возможным новым симплексом. Исходный симплекс имеет полужирную схему. Итерации продолжают, пока они не соответствуют останавливающемуся критерию.