Безусловная минимизация является задачей нахождения векторный x, который является локальным минимумом к скалярной функции f (x):
Неограниченный термин означает, что никакое ограничение не установлено для области значений x.
fminunc trust-region АлгоритмМногие методы, используемые в решателях Optimization Toolbox™, основаны на доверительных областях, простой все же мощной концепции в оптимизации.
Чтобы изучить подход доверительной области к оптимизации, рассмотрите задачу безусловной минимизации, минимизируйте f (x), где функция берет аргументы вектора и возвращает скаляры. Предположим, что вы - в точке x в n - пробел, и вы хотите улучшиться, т.е. переместиться в точку с более низким значением функции. Основная идея состоит в том, чтобы аппроксимировать f более простым функциональным q, который обоснованно отражает поведение функционального f в окружении N вокруг точки x. Это окружение является доверительной областью. Испытательный шаг s вычисляется путем минимизации (или приблизительно минимизации) по N. Это - подпроблема доверительной области,
| (1) |
Текущая точка обновляется, чтобы быть x + s если f (x + s) < f (x); в противном случае текущая точка остается неизменной, и N, область доверия, уменьшается, и испытательный расчет шага повторяется.
Ключевые вопросы в определении определенного подхода доверительной области к минимизации f (x) состоят в том, как выбрать и вычислить приближение q (заданный в текущей точке x), как выбрать и изменить доверительную область N, и как точно решить подпроблему доверительной области. Этот раздел фокусируется на неограниченной проблеме. Более поздние разделы обсуждают дополнительные осложнения из-за присутствия ограничений на переменные.
В стандартном методе доверительной области ([48]), квадратичное приближение q задан первыми двумя терминами приближения Тейлора к F в x; окружение N является обычно сферическим или эллипсоидальным в форме. Математически подпроблема доверительной области обычно утверждается
| (2) |
где g является градиентом f в текущей точке x, H является матрицей Гессиана (симметрическая матрица вторых производных), D является диагональной матрицей масштабирования, Δ является положительной скалярной величиной и ∥. ∥ является 2-нормой. Хорошие алгоритмы существуют для решения уравнения 2 (см. [48]); такие алгоритмы обычно включают расчет всех собственных значений H, и процесс Ньютона применился к характеристическому уравнению
Такие алгоритмы предоставляют точное решение уравнения 2. Однако они требуют времени, пропорционального нескольким факторизациям H. Поэтому для крупномасштабных проблем другой подход необходим. Несколько приближений и эвристических стратегий, на основе уравнения 2, были предложены в литературе ([42] и [50]). Подход приближения, сопровождаемый в решателях Optimization Toolbox, должен ограничить подпроблему доверительной области двумерным подпространством S ([39] и [42]). Однажды подпространство S был вычислен, работа, чтобы решить уравнение 2 тривиальна, даже если полная информация о собственном значении/собственном векторе необходима (поскольку в подпространстве, проблема только двумерна). Доминирующая работа теперь переключила к определению подпространства.
Двумерное подпространство S определяется при помощи предобусловленного процесса метода сопряженных градиентов, описанного ниже. Решатель задает S как линейный пробел, заполненный s 1 и s 2, где s 1 является в направлении градиента g, и s 2 является любой аппроксимированным направлением Ньютона, i.e., решение
| (3) |
или направление отрицательной кривизны,
| (4) |
Философия позади этого выбора S должна обеспечить глобальную сходимость (через направление наискорейшего спуска или направление отрицательной кривизны) и достигнуть быстро локальной сходимости (через шаг Ньютона, когда это существует).
Эскиз безусловной минимизации с помощью идей доверительной области теперь легко дать:
Сформулируйте двумерную подпроблему доверительной области.
Решите уравнение 2, чтобы определить испытательный шаг s.
Если f (x + s) <f (x), то x = x + s.
Настройте Δ.
Эти четыре шага повторяются до сходимости. Размерность доверительной области Δ настроена согласно стандартным правилам. В частности, это уменьшено, если испытательный шаг не принят, т.е. f (x + s) ≥ f (x). См. [46] и [49] для обсуждения этого аспекта.
Решатели Optimization Toolbox обрабатывают несколько важных особых случаев f со специализированными функциями: нелинейный метод наименьших квадратов, квадратичные функции и линейный метод наименьших квадратов. Однако базовые алгоритмические идеи эквивалентны для общего случая. Эти особые случаи обсуждены в более поздних разделах.
Популярным способом решить большие, симметричные, положительные определенные системы линейных уравнений Hp = –g является метод Предобусловленных методов сопряженных градиентов (PCG). Этот итерационный подход требует способности вычислить матричные векторные произведения формы H·v, где v является произвольным вектором. Симметричный положительный определенный матричный M является предварительным формирователем для H. Таким образом, M = C2, где C–1HC–1 хорошо подготовленная матрица или матрица с кластеризованными собственными значениями.
В контексте минимизации можно принять, что матрица Гессиана H симметрична. Однако H, как гарантируют, будет положителен определенный только в окружении сильного минимизатора. PCG алгоритма выходит, когда он сталкивается с направлением отрицательных (или нуль) искривление, то есть, dTHD ≤ 0. PCG направление выхода p является или направлением отрицательной кривизны или приближенным решением системы Ньютона Hp = –g. В любом случае p помогает задать двумерное подпространство, используемое в подходе доверительной области, обсужденном в Методах Доверительной области для Нелинейной Минимизации.
fminunc quasi-newton АлгоритмНесмотря на то, что широкий спектр методов существует для оптимизации без ограничений, методы могут быть широко категоризированы в терминах производной информации или нет, используются. Методы поиска, которые используют только вычисления функции (e.g., симплексный поиск Nelder и Mead [30]), наиболее подходят для проблем, которые не являются гладкими или имеют много разрывов. Градиентные методы обычно более эффективны, когда функция, которая будет минимизирована, непрерывна в ее первой производной. Методы высшего порядка, такие как метод Ньютона, только действительно подходят, когда информация второго порядка с готовностью и легко вычисляется, потому что вычисление информации второго порядка, с помощью числового дифференцирования, является в вычислительном отношении дорогим.
Градиентные методы используют информацию о наклоне функции, чтобы продиктовать направление поиска, где минимум, как думают, лежит. Самым простым из них является метод быстрейшего спуска, в котором поиск выполняется в направлении, – ∇f (x), где ∇f (x) является градиентом целевой функции. Этот метод очень неэффективен, когда функция, которая будет минимизирована, имеет длинные узкие овраги, когда, например, имеет место для функции Розенброка
| (5) |
Минимум этой функции в x = [1,1], где f (x) = 0. Контурная карта этой функции показана на рисунке ниже, наряду с путем к решению к минимуму для реализации наискорейшего спуска, запускающейся в точке [-1.9,2]. Оптимизация была отключена после 1 000 итераций, все еще значительное расстояние от минимума. Черные области - то, где метод постоянно делает зигзаги с одной стороны оврага другому. Обратите внимание на то, что к центру графика, много больших шагов сделаны, когда точка приземляется точно в центре оврага.
Рисунок 5-1, метод быстрейшего спуска для функции Розенброка
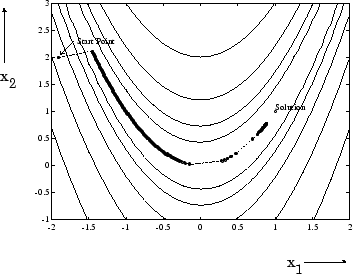
Эта функция, также известная как банановую функцию, известна в неограниченных примерах из-за способа, которым искривление изгибается вокруг источника. Функция Розенброка используется в этом разделе, чтобы проиллюстрировать использование множества методов оптимизации. Контуры были построены с экспоненциальным шагом из-за крутизны наклона, окружающего U-образный овраг.
Для большего количества полного описания этого рисунка, включая скрипты, которые генерируют итеративные точки, смотрите Банановую Минимизацию Функции.
Из методов, которые используют информацию о градиенте, самыми привилегированными являются приближенные методы ньютона. Эти методы создают информацию об искривлении в каждой итерации, чтобы сформулировать квадратичную проблему модели формы
| (6) |
где матрица Гессиана, H, является положительной определенной симметрической матрицей, c является постоянным вектором, и b является константой. Оптимальное решение для этой проблемы происходит, когда частные производные x переходят к нулю, i.e.,
| (7) |
Точка оптимального решения, x*, может быть записана как
| (8) |
Методы типа ньютона (в противоположность приближенным методам ньютона) вычисляют H непосредственно и продолжают в направлении спуска определять местоположение минимума после многих итераций. Вычисление H численно включает большой объем расчета. Приближенные методы ньютона избегают этого при помощи наблюдаемого поведения f (x) и ∇f (x), чтобы создать информацию об искривлении, чтобы сделать приближение к H с помощью соответствующего метода обновления.
Большое количество методов обновления Гессиана было разработано. Однако формула Broyden [3], Флетчер [12], Goldfarb [20] и Shanno [37] (BFGS), как думают, является самой эффективной для использования в методе общего назначения.
Формула, данная BFGS,
| (9) |
где
Как начальная точка, H 0 может быть установлен в любую симметричную положительную определенную матрицу, например, единичная матрица I. Чтобы избежать инверсии Гессиана H, можно вывести метод обновления, который избегает прямой инверсии H при помощи формулы, которая делает приближение обратного Гессиана H–1 при каждом обновлении. Известная процедура является формулой DFP Davidon [7], Флетчера и Пауэлла [14]. Это использует ту же формулу в качестве метода BFGS (уравнение 9) за исключением того, что qk заменяют sk.
Информация градиента или предоставлена через аналитически расчетные градиенты или выведена частными производными с помощью числового метода дифференцирования через конечные разности. Это включает беспокойство каждой из переменных проекта, x, в свою очередь и вычисления скорости изменения в целевой функции.
В каждой главной итерации, k, поиск линии выполняется в направлении
| (10) |
Приближенный метод ньютона проиллюстрирован путем к решению на функции Розенброка в рисунке 5-2, Методе BFGS на Функции Розенброка. Метод может следовать за формой оврага и сходится к минимуму после 140 вычислений функции с помощью только градиенты конечной разности.
Рисунок 5-2, метод BFGS на функции Розенброка
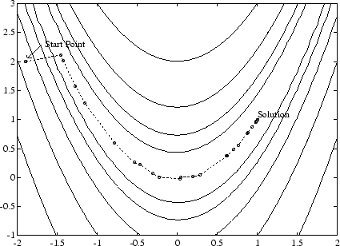
Для большего количества полного описания этого рисунка, включая скрипты, которые генерируют итеративные точки, смотрите Банановую Минимизацию Функции.
Поиск линии является методом поиска, который используется в качестве части большего алгоритма оптимизации. На каждом шаге основного алгоритма метод поиска линии ищет вдоль линии, содержащей текущую точку, xk, параллельный поисковому направлению, которое является вектором, определенным основным алгоритмом. Таким образом, метод находит, что следующие выполняют итерации x k +1 из формы
| (11) |
где xk обозначает, что ток выполняет итерации, dk является поисковым направлением, и α* является скалярным параметром длины шага.
Метод поиска линии пытается уменьшить целевую функцию вдоль линии xk + α *dk путем повторной минимизации моделей полиномиальной интерполяции целевой функции. Процедура поиска линии имеет два основных шага:
Фаза заключения в скобки определяет область значений точек на линии искаться. Скобка соответствует интервалу, указывающему диапазон значений α.
Шаг разделения делит скобку на подынтервалы, на которых минимум целевой функции аппроксимирован полиномиальной интерполяцией.
Получившаяся длина шага α удовлетворяет условиям Вольфа:
| (12) |
| (13) |
где c 1 и c 2 является константами с 0 <c 1 <c 2 <1.
Первое условие (уравнение 12) требует, чтобы αk достаточно уменьшил целевую функцию. Второе условие (уравнение 13) гарантирует, что длина шага не слишком мала. Точки, которые удовлетворяют обоим условиям ( Уравнение 12 и уравнение 13) называются приемлемыми точками.
Метод поиска линии является реализацией алгоритма, описанного в Разделе 2-6 из [13]. См. также [31] для получения дополнительной информации о поиске линии.
Многие оптимизационные функции определяют направление поиска путем обновления матрицы Гессиана в каждой итерации, использования метода BFGS (уравнение 9). Функция fminunc также предоставляет возможность использовать метод DFP, данный в Приближенных методах ньютона (установите HessUpdate к 'dfp' в options выбрать метод DFP). Гессиан, H, всегда обеспечивается, чтобы быть положителен определенный так, чтобы направление поиска, d, всегда было в направлении спуска. Это означает, что для некоторого произвольно небольшого шага α в направлении d, целевая функция уменьшается в величине. Вы достигаете положительной определенности H путем гарантирования, что H инициализируется, чтобы быть положителен определенный и после этого (от уравнения 14), всегда положительно. Термин продукт параметра длины шага поиска линии αk и комбинация поискового направления d с прошлыми и настоящими оценками градиента,
| (14) |
Вы всегда достигаете условия это положительно путем выполнения достаточно точного поиска линии. Это вызвано тем, что поисковое направление, d, является направлением спуска, так, чтобы αk и отрицательный градиент – ∇f (xk)Td всегда положительны. Таким образом, возможный отрицательный термин – ∇f (x k +1)Td может быть сделан столь же маленьким в величине как требуется путем увеличения точности поиска линии.