Удалите контуры между субдоменами
[ удаляет контуры между субдоменами, заданными в dl1,bt1] = csgdel(dl,bt,bl)bl. При удалении контуров в bl делает анализируемую матрицу геометрии противоречивой, затем csgdel удаляет дополнительные сегменты границы (сегменты ребра между субдоменами), чтобы сохранить непротиворечивость.
Удаление контуров обычно изменяет идентификаторы ребра остающихся контуров.
csgdel не удаляет граничные сегменты (внешние границы).
Удалите ребра в 2D геометрии, созданной в приложении PDE Modeler и экспортируемой в MATLAB® рабочая область.
Создайте геометрию в приложении PDE Modeler путем ввода следующих команд в командное окно MATLAB:
pdecirc(0,0,1,'C1') pdecirc(0,0,0.5,'C2') pderect([-0.2 0.2 0.2 0.9],'R1') pderect([0 1 0 1],'SQ1')
Уменьшайте геометрию до первого квадранта путем пересечения его с квадратом. Для этого введите (C1+C2+R1)*SQ1 в поле Set formula.
Из приложения PDE Modeler экспортируйте матрицу описания геометрии, установите формулу и матрицу пространства имен к рабочему пространству MATLAB путем выбора Export Geometry Description, Set Formula, Labels из меню Draw.
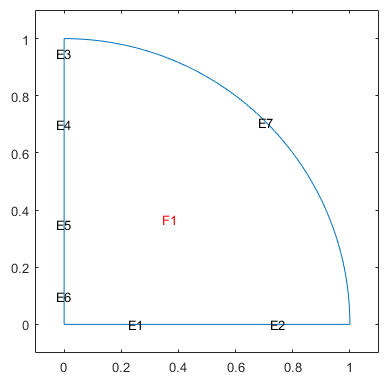
В командном окне MATLAB используйте decsg функция, чтобы разложить экспортируемую геометрию на минимальные области. Это создает AnalyticGeometry объект dl. Постройте dl.
[dl,bt] = decsg(gd,sf,ns); pdegplot(dl,'EdgeLabels','on','FaceLabels','on') xlim([-0.1 1.1]) ylim([-0.1 1.1])
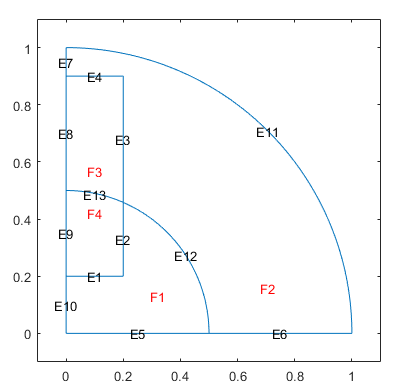
Удалите ребра 1, 2, и 13 использований csgdel функция. Задайте ребра, чтобы удалить как вектор из идентификаторов ребра. Постройте получившуюся геометрию.
[dl1,bt1] = csgdel(dl,bt,[1 2 13]); pdegplot(dl1,'EdgeLabels','on','FaceLabels','on') xlim([-0.1 1.1]) ylim([-0.1 1.1])
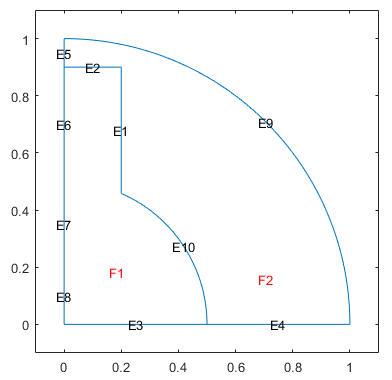
Теперь удалите все контуры между субдоменами и постройте получившуюся геометрию.
[dl1,bt1] = csgdel(dl,bt); pdegplot(dl1,'EdgeLabels','on','FaceLabels','on') xlim([-0.1 1.1]) ylim([-0.1 1.1])
dl — Анализируемая матрица геометрииАнализируемая матрица геометрии, возвращенная как матрица чисел с двойной точностью. Это содержит представление анализируемой геометрии в терминах разделенных минимальных областей, созданных decsg алгоритм. Каждый сегмент ребра минимальных областей соответствует столбцу в dl. Сегменты ребра между минимальными областями (субдомены) являются сегментами границы. Внешние границы являются граничными сегментами. В каждом столбце вторые и третьи строки содержат запуск и окончание x - координаты. Четвертые и пятые строки содержат соответствующий y - координаты. Шестые и седьмые строки содержат левые и правые минимальные метки области относительно направления, вызванного начальными и конечными точками (направление против часовой стрелки на круге и сегментах эллипса). Существует три типа возможных сегментов ребра в минимальной области:
Для круговых сегментов ребра первой строкой является 1. Восьмые и девятые строки содержат координаты центра круга. 10-я строка содержит радиус.
Для сегментов ребра линии первой строкой является 2.
Для сегментов ребра эллипса первой строкой является 4. Восьмые и девятые строки содержат координаты центра эллипса. 10-е и 11-е строки содержат полуоси эллипса. 12-я строка содержит вращательный угол эллипса.
Все столбцы в анализируемой матрице геометрии имеют одинаковое число строк. Строки, которые не требуются для конкретной формы, заполнены нулями.
| Номер строки | Круговой сегмент ребра | Сегмент ребра линии | Сегмент ребра эллипса |
|---|---|---|---|
| 1 | 1 | 2 | 4 |
| 2 | запуск x - координата | запуск x - координата | запуск x - координата |
| 3 | окончание x - координата | окончание x - координата | окончание x - координата |
| 4 | запуск y - координата | запуск y - координата | запуск y - координата |
| 5 | окончание y - координата | окончание y - координата | окончание y - координата |
| 6 | оставленная минимальная метка области | оставленная минимальная метка области | оставленная минимальная метка области |
| 7 | правильная минимальная метка области | правильная минимальная метка области | правильная минимальная метка области |
| 8 | x- центра | x- центра | |
| 9 | y- центра | y- центра | |
| 10 | радиус круга | x- перед вращением | |
| 11 | y- перед вращением | ||
| 12 | Угол в радианах между x - ось и первой полуосью |
Типы данных: double
bt — Булева таблица, связывающая исходные формы с минимальными областямиБулева таблица, связывающая исходные формы с минимальными областями, возвращенными как матрица 1 с и 0s.
Типы данных: double
bl — Контуры, чтобы удалитьКонтуры, чтобы удалить в виде положительного целого числа или вектора из положительных целых чисел. Каждое целое число представляет граничный ID.
Типы данных: double
dl1 — Измененная анализируемая матрица геометрииИзмененная анализируемая матрица геометрии, возвращенная как матрица чисел с двойной точностью.
Типы данных: double
bt1 — Булева табличная связь, остающаяся исходные формы в минимальные областиБулева таблица, связывающая остающиеся исходные формы с минимальными областями, возвращенными как матрица 1 с и 0s.
Типы данных: double
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.