Твердый кабелепровод для потока газа
Simscape / Библиотека Основы / Газ / Элементы
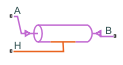
Модели блока Pipe (G) передают динамику потока по каналу в газовой сети. Блок вычисляет вязкие потери на трение и конвективную теплопередачу со стеной трубопровода. Трубопровод содержит постоянный объем газа. Давление и температура развивается на основе сжимаемости и тепловой способности этого объема газа. Дросселирование появляется, когда выход достигает звукового условия.
Внимание
Поток газа через этот блок может дросселировать. Если блок Mass Flow Rate Source (G) или блок Controlled Mass Flow Rate Source (G), соединенный с блоком Pipe (G), задают больший массовый расход жидкости, чем возможный дросселируемый массовый расход жидкости, вы получаете ошибку симуляции. Для получения дополнительной информации смотрите Дросселируемый Поток.
Массовое сохранение связывает массовые расходы жидкости с динамикой давления и температуры внутреннего узла, представляющего объем газа:
где:
частная производная массы объема газа относительно давления при постоянной температуре и объеме.
частная производная массы объема газа относительно температуры при постоянном давлении и объеме.
p я - давление объема газа.
T я - температура объема газа.
t время.
A и B являются массовыми расходами жидкости в портах А и B, соответственно. Скорость потока жидкости, сопоставленная с портом, положительна, когда она течет в блок.
Энергосбережение связывает энергию и уровни теплового потока к динамике давления и температуры внутреннего узла, представляющего объем газа:
где:
частная производная внутренней энергии объема газа относительно давления при постоянной температуре и объеме.
частная производная внутренней энергии объема газа относительно температуры при постоянном давлении и объеме.
Φ A и Φ B является энергетическими скоростями потока жидкости в портах A и B, соответственно.
Q H является уровнем теплового потока в порте H.
Частные производные массового M и внутренней энергии U объема газа, относительно давления и температуры в постоянном объеме, зависят от газовой модели свойства. Для совершенных и полусовершенных газовых моделей уравнения:
где:
ρ я - плотность объема газа.
V является объемом газа.
h я - определенная энтальпия объема газа.
Z является фактором сжимаемости.
R является определенной газовой константой.
Пи c является удельной теплоемкостью при постоянном давлении объема газа.
Для действительной газовой модели, частных производных массового M и внутренней энергии U объема газа, относительно давления и температуры в постоянном объеме:
где:
β является изотермическим модулем объемной упругости объема газа.
α является изобарным тепловым коэффициентом расширения объема газа.
Баланс импульса для каждой половины трубопровода моделирует перепад давления из-за потока импульса и вязкого трения:
где:
p является давлением газа в порте A, порте B или внутреннем узле I, как обозначено индексом.
ρ является плотностью в порте A, порте B или внутреннем узле I, как обозначено индексом.
S является площадью поперечного сечения трубопровода.
AI Δp и BI Δp являются падением давления из-за вязкого трения.
Тепло, которым обмениваются со стеной трубопровода через порт H, добавляется к энергии объема газа, представленного внутренним узлом через уравнение энергосбережения (см. энергетический Баланс). Поэтому балансы импульса для каждой половины трубопровода, между портом A и внутренним узлом и между портом B и внутренним узлом, приняты, чтобы быть адиабатическими процессами. Адиабатические отношения:
где h является определенной энтальпией в порте A, порте B или внутреннем узле I, как обозначено индексом.
Падение давления из-за вязкого трения, AI Δp и BI Δp, зависит от режима течения. Числа Рейнольдса для каждой половины трубопровода заданы как:
где:
D h является гидравлическим диаметром трубопровода.
μ я - динамическая вязкость во внутреннем узле.
Если число Рейнольдса меньше значения параметров Laminar flow upper Reynolds number limit, то поток находится в ламинарном режиме течения жидкости. Если число Рейнольдса больше значения параметров Turbulent flow lower Reynolds number limit, то поток находится в режиме турбулентного течения.
В ламинарном режиме течения жидкости падение давления из-за вязкого трения:
где:
Форма f является значением параметров Shape factor for laminar flow viscous friction.
L eqv является значением параметров Aggregate equivalent length of local resistances.
В режиме турбулентного течения падение давления из-за вязкого трения:
где f Дарси является коэффициентом трения Дарси в порте A или B, как обозначено индексом.
Коэффициенты трения Дарси вычисляются из корреляции Haaland:
где ε грубо является значением параметров Internal surface absolute roughness.
Когда число Рейнольдса между Laminar flow upper Reynolds number limit и значениями параметров Turbulent flow lower Reynolds number limit, поток находится в переходе между ламинарным течением и турбулентным течением. Падение давления из-за вязкого трения во время области перехода следует за сглаженной связью между теми в ламинарном режиме течения жидкости и теми в режиме турбулентного течения.
Конвективное уравнение теплопередачи между стеной трубопровода и внутренним объемом газа:
Surf S является площадью поверхности трубопровода, surf S = 4SL/Dh. Принимая экспоненциальное температурное распределение вдоль трубопровода, конвективная теплопередача
где:
T в является входной температурой в зависимости от направления потока.
средний массовый расход жидкости от порта A до порта B.
удельная теплоемкость, оцененная при средней температуре.
Коэффициент теплопередачи, коэффициент h, зависит от номера Nusselt:
где k в среднем является теплопроводностью, оцененной при средней температуре. Номер Nusselt зависит от режима течения. Номер Nusselt в ламинарном режиме течения жидкости является постоянным и равным значению параметра Nusselt number for laminar flow heat transfer. Номер Nusselt в режиме турбулентного течения вычисляется из корреляции Гниелинского:
где Pr в среднем является числом Прандтля, оцененным при средней температуре. Среднее число Рейнольдса
где μ в среднем является динамической вязкостью, оцененной при средней температуре. Когда среднее число Рейнольдса между Laminar flow upper Reynolds number limit и значениями параметров Turbulent flow lower Reynolds number limit, номер Nusselt следует за плавным переходом между ламинарными и турбулентными числовыми значениями Nusselt.
Дросселируемые массовые расходы жидкости из трубопровода в портах A и B:
где a A и a B является скоростью звука в портах A и B, соответственно.
Недросселируемое давление в порте A или B является значением соответствующей переменной Across в том порте:
Дросселируемые давления в портах A и B получены путем замены дросселируемыми массовыми расходами жидкости в уравнения баланса импульса для трубопровода:
AIchoked Δp и Δp, BIchoked являются падением давления из-за вязкого трения, принимая, что дросселирование появилось. Они вычисляются похожие на AI Δp и BI Δp с массовыми расходами жидкости в портах A и B, замененных дросселируемыми значениями массового расхода жидкости.
В зависимости от того, появилось ли дросселирование, блок присваивает или дросселируемое или недросселируемое значение давления как фактическое давление в порте. Дросселирование может появиться при выходе трубопровода, но не во входе трубопровода. Поэтому, если p Aunchoked ≥ p I, то порт A является входом и p = p Aunchoked. Если p Aunchoked <p I, то порт A является выходом и
Точно так же, если p Bunchoked ≥ p I, то порт B является входом и p B = p Bunchoked. Если p Bunchoked <p I, то порт B является выходом и
Чтобы установить приоритет и начальные целевые значения для переменных в блоках до симуляции, используйте вкладку Variables в диалоговом окне блока (или раздел Variables в блоке Property Inspector). Для получения дополнительной информации смотрите Приоритет Набора и Начальную Цель для Переменных в блоках и Начальные условия для Блоков с Конечным Объемом газа.
Стена трубопровода совершенно тверда.
Поток полностью разрабатывается. Потери на трение и теплопередача не включают эффекты входа.
Эффект силы тяжести незначителен.
Инерция жидкости незначительна.
Этот блок не моделирует сверхзвуковой поток.
[1] Белый, F. M. гидроаэромеханика. 7-й Эд, разделите 6.8. McGraw-Hill, 2011.
[2] Cengel, Y. A. теплопередача и перемещение массы – практический подход. 3-й Эд, разделите 8.5. McGraw-Hill, 2007.