BLDC

Бесщеточный двигатель постоянного тока с тремя обмотками с трапециевидным распределением потока

Библиотека:
Simscape / Электрический / Электромеханический / Постоянный магнит

Описание

Блок BLDC моделирует постоянный магнит синхронная машина с трехфазным статором раны Уая. Блок имеет четыре опции для определения распределения потока постоянного магнита в зависимости от угла ротора. Две опции допускают простую параметризацию путем принятия совершенного трапецоида для коэффициента противо-ЭДС. Для простой параметризации вы задаете или потокосцепление или вызванный ротором коэффициент противо-ЭДС. Другие две опции дают более точные результаты с помощью табличных данных, которые вы задаете. Для более точных результатов вы задаете или частную производную потокосцепления или измеренный коэффициент противо-ЭДС, постоянную для данной скорости ротора.

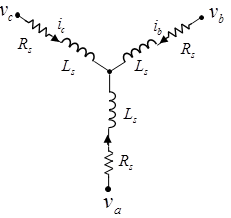
Рисунок показывает эквивалентную электрическую схему для обмоток статора.

Моторная конструкция

Этот рисунок показывает моторную конструкцию с однополюсно-парным на роторе.

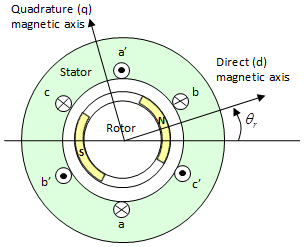
Для соглашения осей на предыдущем рисунке a - выравниваются фаза и потоки постоянного магнита, когда угол ротора _θr является нулем. Блок поддерживает второе определение оси ротора. Для второго определения угол ротора является углом между a - фазой магнитная ось и ротором q - ось.

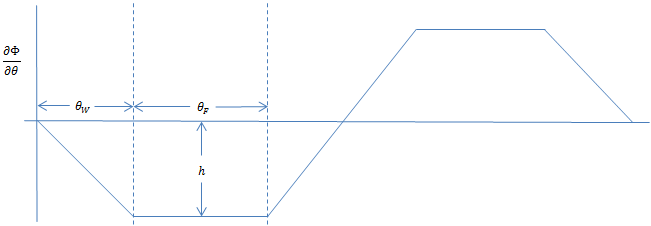
Трапециевидная скорость изменения потока

Магнитное поле ротора из-за постоянных магнитов создает трапециевидную скорость изменения потока с углом ротора. Рисунок показывает эту скорость изменения потока.

Коэффициент противо-ЭДС является скоростью изменения потока, заданного

$\frac{d Φ}{d t} = \frac{\partial Φ}{\partial θ} \frac{d θ}{d t} = \frac{\partial Φ}{\partial θ} ω,$

где:

Φ является потокосцеплением постоянного магнита.
θ является углом ротора.
ω является скоростью вращательного механического устройства.

Высота h из трапециевидной скорости изменения потока профиль выведен из потока пика постоянного магнита.

Интеграция $\frac{\partial Φ}{\partial θ}$ в области значений 0 к π/2,

$Φ_{m a x} = \frac{h}{2} (θ_{F} + θ_{W}),$

где:

_Φmax является потокосцеплением постоянного магнита.
h является скоростью изменения высоты профиля потока.
_θF является углом ротора, передвигаются, по которому, коэффициент противо-ЭДС что поток постоянного магнита вызывает в статоре, является постоянным.
_θW является углом ротора, передвигаются, по которым увеличениям коэффициента противо-ЭДС или уменьшается линейно, когда ротор перемещается в постоянную скорость.

Реорганизация предыдущего уравнения,

$h = 2 Φ_{m a x} / (θ_{F} + θ_{W}) .$

Электрические уравнения определения

Напряжения через обмотки статора заданы

$[\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}] = [\begin{matrix} R_{s} & 0 & 0 \\ 0 & R_{s} & 0 \\ 0 & 0 & R_{s} \end{matrix}] [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] + [\begin{matrix} \frac{d ψ_{a}}{d t} \\ \frac{d ψ_{b}}{d t} \\ \frac{d ψ_{c}}{d t} \end{matrix}],$

где:

_va, _vb и _vc являются внешними напряжениями, применился к трем моторным электрическим соединениям.
_Rs является эквивалентным сопротивлением каждой обмотки статора.
_ia, _ib и _ic являются токами, текущими в обмотках статора.
$\frac{d ψ_{a}}{d t},$ $\frac{d ψ_{b}}{d t},$ и $\frac{d ψ_{c}}{d t}$

скорости изменения магнитного потока в каждой обмотке статора.

Постоянный магнит и эти три обмотки способствуют общему потоку, соединяющему каждую обмотку. Общий поток задан

$[\begin{matrix} ψ_{a} \\ ψ_{b} \\ ψ_{c} \end{matrix}] = [\begin{matrix} L_{a a} & L_{a b} & L_{a c} \\ L_{b a} & L_{b b} & L_{b c} \\ L_{c a} & L_{c b} & L_{c c} \end{matrix}] [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] + [\begin{matrix} ψ_{a m} \\ ψ_{b m} \\ ψ_{c m} \end{matrix}],$

где:

_ψa, _ψb и _ψc являются общими потоками, соединяющими каждую обмотку статора.
_Laa, _Lbb и _Lcc являются самоиндукциями обмоток статора.
_Lab, _Lac, _Lba, и т.д. является взаимной индуктивностью обмоток статора.
_ψam, _ψbm и _ψcm являются потоками постоянного магнита, соединяющими обмотки статора.

Индуктивность в обмотках статора является функциями угла ротора, заданного

$L_{a a} = L_{s} + L_{m} cos (2 θ_{r}),$

$L_{b b} = L_{s} + L_{m} cos (2 (θ_{r} - 2 π / 3)),$

$L_{c c} = L_{s} + L_{m} cos (2 (θ_{r} + 2 π / 3)),$

$L_{a b} = L_{b a} = - M_{s} - L_{m} \cos (2 (θ_{r} + π / 6)),$

$L_{b c} = L_{c b} = - M_{s} - L_{m} \cos (2 (θ_{r} + π / 6 - 2 π / 3)),$

$L_{c a} = L_{a c} = - M_{s} - L_{m} \cos (2 (θ_{r} + π / 6 + 2 π / 3)),$

где:

_Ls является самоиндукцией статора на фазу — средняя самоиндукция каждой из обмоток статора.
_Lm является колебанием индуктивности статора — колебание самоиндукции и взаимной индуктивности с изменяющимся углом ротора.
_Ms является статором взаимная индуктивность — средняя взаимная индуктивность между обмотками статора.

Поток постоянного магнита, соединяющий каждую обмотку статора, следует за трапециевидным показанным на рисунке профилем. Блок реализует трапециевидный профиль с помощью интерполяционных таблиц, чтобы вычислить значения потока постоянного магнита.

Упрощенные уравнения

Напряжение определения и уравнения крутящего момента для блока

$[\begin{matrix} v_{d} \\ v_{q} \\ v_{0} \end{matrix}] = P ([\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}] - N ω [\begin{matrix} \frac{\partial ψ_{a m}}{\partial θ_{r}} \\ \frac{\partial ψ_{b m}}{\partial θ_{r}} \\ \frac{\partial ψ_{c m}}{\partial θ_{r}} \end{matrix}]),$

$v_{d} = R_{s} i_{d} + L_{d} \frac{d i_{d}}{d t} - N ω i_{q} L_{q},$

$v_{q} = R_{s} i_{q} + L_{q} \frac{d i_{q}}{d t} + N ω i_{d} L_{d},$

$v_{0} = R_{s} i_{0} + L_{0} \frac{d i_{0}}{d t},$

$T = \frac{3}{2} N (i_{q} i_{d} L_{d} - i_{d} i_{q} L_{q}) + [\begin{matrix} i_{a} & i_{b} & i_{c} \end{matrix}] [\begin{matrix} \frac{\partial ψ_{a m}}{\partial θ_{r}} \\ \frac{\partial ψ_{b m}}{\partial θ_{r}} \\ \frac{\partial ψ_{c m}}{\partial θ_{r}} \end{matrix}],$

где:

_vd, _vq и _v0 является d - ось, q - ось и напряжения нулевой последовательности.
P является Преобразованием Парка, заданным
$P = 2 / 3 [\begin{matrix} \cos θ_{e} & \cos (θ_{e} - 2 π / 3) & \cos (θ_{e} + 2 π / 3) \\ - \sin θ_{e} & - \sin (θ_{e} - 2 π / 3) & - \sin (θ_{e} + 2 π / 3) \\ 0.5 & 0.5 & 0.5 \end{matrix}]$
N является количеством пар полюса постоянного магнита ротора.
ω является скоростью вращательного механического устройства ротора.
$\frac{\partial ψ_{a m}}{\partial θ_{r}},$ $\frac{\partial ψ_{b m}}{\partial θ_{r}},$ и $\frac{\partial ψ_{c m}}{\partial θ_{r}}$

частные производные мгновенного потока постоянного магнита, соединяющего каждую обмотку фазы.
_id, _iq и _i0 является d - ось, q - ось и токи нулевой последовательности, заданные
$[\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}] = P [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] .$
_Ld = _Ls + _Ms + 3/2 _Lm. _Ld является статором d - составляющая индукции.
_Lq = _Ls + _Ms − 3/2 _Lm. _Lq является статором q - составляющая индукции.
_L0 = _Ls – 2_Ms. _L0 является индуктивностью нулевой последовательности статора.
T является крутящим моментом ротора. Крутящий момент течет из моторного случая (блокируйте физический порт C) к моторному ротору (блокируют физический порт R).

Вычисление потерь в железе

Потери в железе разделены на два термина, одно представление основного пути к намагничиванию и другое представление перекрестного зубного пути к совету, который становится активным во время ослабленной операции поля. Модель потерь в железе, которая основана на работе Меллора [3].

Термин, представляющий основной путь к намагничиванию, зависит от вызванного напряжения статора RMS, $V_{m_{r m s}}^{}$ :

$P_{O C} (V_{m_{r m s}}^{}) = \frac{a_{h}}{k} V_{m_{r m s}}^{} + \frac{a_{j}}{k^{2}} V_{m_{r m s}}^{2} + \frac{a_{e x}}{k^{1.5}} V_{m_{r m s}}^{1.5}$

Это - доминирующий термин во время операции без загрузок. k является коэффициентом противо-ЭДС, постоянной, связывающим вольты RMS на Гц. Это задано как $k = V_{m_{r m s}}^{} / f$ , где f является электрической частотой. Первый термин на правой стороне является магнитной гистерезисной потерей, второй является потеря токов Фуко, и третьей является избыточная потеря. Эти три коэффициента, появляющиеся на числителях, выведены из значений, что вы предусматриваете гистерезис разомкнутой цепи, вихрь и избыточные потери.

Термин, представляющий перекрестный зубной путь к совету, становится важным, когда поле размагничивания создано и может быть определено из теста короткой схемы анализа конечных элементов. Это зависит от эдс RMS, сопоставленной с перекрестным зубным потоком совета, $V_{d_{r m s}}^{*}$ :

$P_{S C} (V_{d_{r m s}}^{*}) = \frac{b_{h}}{k} V_{d_{r m s}}^{*} + \frac{b_{j}}{k^{2}} V_{d_{r m s}}^{* 2} + \frac{b_{e x}}{k^{1.5}} V_{d_{r m s}}^{* 1.5}$

Три термина числителя выведены из значений, вы предусматриваете гистерезис короткой схемы, вихрь и избыточные потери.

Предопределенная параметризация

Существует несколько доступной встроенной параметризации для блока BLDC.

Эти данные перед параметризацией позволяют вам настраивать блок, чтобы представлять компоненты определенными поставщиками. Параметризация этих бесщеточных двигателей постоянного тока совпадает с таблицами данных производителя. Чтобы загрузить предопределенную параметризацию, нажмите на гиперссылку Select a predefined parameterization в маске блока BLDC и выберите часть, которую вы хотите использовать из списка доступных компонентов.

Примечание

Предопределенная параметризация компонентов Simscape использует доступные источники данных для предоставления значений параметров. Техническое решение и упрощение предположений используются, чтобы заполнить для недостающих данных. В результате отклонения между симулированным и фактическим физическим поведением должны ожидаться. Чтобы гарантировать необходимую точность, необходимо подтвердить симулированное поведение против экспериментальных данных и совершенствовать модели компонента по мере необходимости.

Для получения дополнительной информации о предварительной параметризации и для списка доступных компонентов, см. Список Предварительно параметрированных Компонентов.

Тепловые порты

Блок имеет четыре дополнительных тепловых порта, один для каждой из этих трех обмоток и один для ротора. Эти порты скрыты по умолчанию. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите Show thermal port. Это действие отображает тепловые порты на значке блока и отсоединяет параметры Thermal Port и Temperature Dependence. Эти параметры описаны далее на этой странице с описанием.

Используйте тепловые порты, чтобы симулировать эффекты медного сопротивления и потерь в железе, которые преобразовывают электроэнергию в теплоту. Для получения дополнительной информации об использовании тепловых портов в блоках привода смотрите Термальные эффекты Симуляции во Вращательных и Поступательных Приводах.

Переменные

Используйте настройки Variables, чтобы задать приоритет и начальные целевые значения для переменных в блоках перед симуляцией. Для получения дополнительной информации смотрите Приоритет Набора и Начальную Цель для Переменных в блоках.

Порты

Сохранение

развернуть все

`~` — Трехфазный порт
электрический

Расширяемый трехфазный порт.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Composite three-phase ports.

`a` — a - фаза
электрический

Электрический порт сохранения, сопоставленный с a - фаза.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Expanded three-phase ports.

`b` — b - фаза
электрический

Электрический порт сохранения, сопоставленный с b - фаза.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Expanded three-phase ports.

`c` — c - фаза
электрический

Электрический порт сохранения, сопоставленный с c - фаза.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Expanded three-phase ports.

`n` — Нейтральная фаза
электрический

Электрический порт сохранения сопоставлен с нейтральной фазой.

Зависимости

Чтобы включить этот порт, установите Winding Type на Wye-wound и Zero sequence к Include.

`R` — Моторный ротор
механическое устройство

Порт сохранения вращательного механического устройства сопоставлен с моторным ротором.

`C` — Моторный случай
механическое устройство

Порт сохранения вращательного механического устройства сопоставлен с моторным случаем.

`HA` — Обмотка теплового порта
тепловой

Тепловой порт сохранения, сопоставленный с обмоткой A. Для получения дополнительной информации смотрите Тепловые Порты.

`HB` — Обмотка B тепловой порт
тепловой

Тепловой порт сохранения, сопоставленный с обмоткой B. Для получения дополнительной информации смотрите Тепловые Порты.

`HC` — Обмотка C тепловой порт
тепловой

Тепловой порт сохранения, сопоставленный с обмоткой C. Для получения дополнительной информации смотрите Тепловые Порты.

`HR` — Ротор тепловой порт
тепловой

Тепловой порт сохранения сопоставлен с ротором. Для получения дополнительной информации смотрите Тепловые Порты.

Параметры

развернуть все

Ротор

`Electrical connection` — Электрическое соединение
`Composite three-phase ports` (значение по умолчанию) | `Expanded three-phase ports`

Иметь ли составной объект или расширил трехфазные порты.

`Winding type` — Настройка обмоток
`Wye-wound` (значение по умолчанию) | `Delta-wound`

Выберите настройку для обмоток:

Wye-wound — Обмотки являются раной Уая.
Delta-wound — Обмотки являются раной дельты. a - фаза соединяется между портами a и b, b - фазой между портами b и c и c - фаза между портами c и a.

`Back EMF profile` — Профиль Коэффициента противо-ЭДС
`Perfect trapezoid - specify maximum flux linkage` (значение по умолчанию) | `Perfect trapezoid - specify maximum rotor-induced back emf` | `Tabulated - specify flux partial derivative with respect to rotor angle` | `Tabulated - specify rotor-induced back emf as a function of rotor angle`

Параметризация для определения распределения потока постоянного магнита в зависимости от угла ротора. Выберите:

Perfect trapezoid - specify maximum flux linkage задавать максимальное потокосцепление для постоянного магнита и угла ротора, где коэффициент противо-ЭДС является постоянным. Блок принимает совершенный трапецоид для коэффициента противо-ЭДС. Это - значение по умолчанию.
Perfect trapezoid - specify maximum rotor-induced back emf задавать максимум вызванный ротором коэффициент противо-ЭДС и соответствующая скорость ротора. Блок принимает совершенный трапецоид для коэффициента противо-ЭДС.
Tabulated - specify flux partial derivative with respect to rotor angle задавать значения для частной производной потокосцепления и соответствующих углов ротора.
Tabulated - specify rotor-induced back emf as a function of rotor angle задавать измеренный коэффициент противо-ЭДС, постоянную и соответствующую скорость ротора и углы.

`Maximum permanent magnet flux linkage` — Максимальное потокосцепление постоянного магнита
0.03 `Wb` (значение по умолчанию)

Пиковое потокосцепление постоянного магнита с любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Back EMF profile на Perfect trapezoid - specify maximum flux linkage.

`Rotor angle over which back emf is constant` — Угол ротора, по которому коэффициент противо-ЭДС является постоянным
`pi / 12` `rad` (значение по умолчанию)

Угол ротора передвигается, по которому поток постоянного магнита, соединяющий обмотку статора, является постоянным. Этот угол является _θF на рисунке, который показывает Трапециевидную Скорость изменения Потока.

Зависимости

Чтобы включить этот параметр, установите Back EMF profile на Perfect trapezoid - specify maximum flux linkage или Perfect trapezoid - specify maximum rotor-induced back emf.

`Maximum rotor-induced back emf` — Максимум вызванный ротором коэффициент противо-ЭДС
9.6 `V` (значение по умолчанию)

Пик вызванный ротором коэффициент противо-ЭДС в обмотки статора.

Зависимости

Чтобы включить этот параметр, установите Back EMF profile на Perfect trapezoid - specify maximum rotor-induced back emf.

`Rotor-induced back emf` — Вызванный ротором коэффициент противо-ЭДС
[0, -9.6, -9.6, 9.6, 9.6, 0] `V` (значение по умолчанию)

Вектор из значений для вызванного ротором коэффициента противо-ЭДС в зависимости от угла ротора. Первые и последние значения должны быть тем же самым и обычно равны нулю. Для получения дополнительной информации смотрите параметр Corresponding rotor angles. Первые и последние значения являются тем же самым, потому что поток является циклическим с периодом $2 π / N$ , где N является количеством пар полюса постоянного магнита.

Зависимости

Чтобы включить этот параметр, установите Back EMF profile на Tabulated - specify rotor-induced back emf as a function of rotor angle.

`Flux linkage partial derivative with respect to rotor angle` — Частная производная потокосцепления относительно угла ротора
[0, -.1528, -.1528, .1528, .1528, 0] `Wb/rad` (значение по умолчанию)

Вектор из значений для частной производной потокосцепления (где потокосцепление является количеством времен потока обмотки поворотов) относительно угла ротора. Первые и последние значения должны быть тем же самым и обычно равны нулю. Для получения дополнительной информации смотрите параметр Corresponding rotor angles. Первые и последние значения являются тем же самым, потому что поток является циклическим с периодом $2 π / N$ , где N является количеством пар полюса постоянного магнита.

`Corresponding rotor angles` — Соответствующие углы ротора
[0, 7.5, 22.5, 37.5, 52.5, 60] `deg` (значение по умолчанию)

Вектор из углов ротора, где частная производная потокосцепления или вызванный ротором коэффициент противо-ЭДС заданы. Угол ротора задан как угол между a - фазой магнитная ось и d - ось. Таким образом, когда угол является нулем, магнитные поля из-за ротора и a - обмотка фазы выравнивается. Это определение используется независимо от вашей установки блока для углового определения ротора. Первое значение является нулем, и последнее значение $2 π / N$ , где N является количеством пар полюса постоянного магнита.

Зависимости

Чтобы включить этот параметр, установите Back EMF profile на Tabulated - specify flux partial derivative with respect to rotor angle или Tabulated - specify rotor-induced back emf as a function of rotor angle.

`Rotor speed used for back emf measurement` — Скорость ротора используется для измерения коэффициента противо-ЭДС
600 `rpm` (значение по умолчанию)

Задайте скорость ротора, соответствующую максимуму вызванный ротором коэффициент противо-ЭДС.

Зависимости

Чтобы включить этот параметр, установите Back EMF profile на Perfect trapezoid - specify maximum rotor-induced back emf или Tabulated - specify rotor-induced back emf as a function of rotor angle.

`Number of pole pairs` Количество пар полюсов
6 (значение по умолчанию)

Количество постоянного магнита подпирает пары шестами на роторе.

`Rotor angle definition` — Контрольная точка для углового измерения ротора
`Angle between the a-phase magnetic axis and the d-axis` (значение по умолчанию) | `Angle between the a-phase magnetic axis and the q-axis`

Контрольная точка для углового измерения ротора. Значением по умолчанию является Angle between the a-phase magnetic axis and the d-axis. Это определение показывают на Моторном рисунке Конструкции. Когда вы выбираете это значение, ротор и a - потоки фазы выравниваются, когда угол ротора является нулем.

Другим значением, которое можно выбрать для этого параметра, является Angle between the a-phase magnetic axis and the q-axis. Когда вы выбираете это значение, a - текущая фаза генерирует максимальный крутящий момент, когда угол ротора является нулем.

Статор

`Modeling fidelity` — Моделирование точности
`Constant Ld and Lq` (значение по умолчанию) | `Tabulated Ld and Lq`

Выберите точность моделирования:

Constant Ld and Lq — Ld и значения Lq являются постоянными и заданы их соответствующими параметрами.
Tabulated Ld and Lq — Ld и значения Lq вычисляются онлайн из текущих интерполяционных таблиц DQ можно следующим образом:

$L_{d} = f_{1} (i_{d}, i_{q})$

$L_{d} = f_{2} (i_{d}, i_{q})$

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0.

`Stator parameterization` — Параметризация статора
`Specify Ld, Lq, and L0` (значение по умолчанию) | `Specify Ls, Lm, and Ms`

Выберите Specify Ld, Lq, and L0 или Specify Ls, Lm, and Ms.

`Stator d-axis inductance, Ld` — D-составляющая-индукции статора
0.00022 `H` (значение по умолчанию)

D-составляющая-индукции.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Constant Ld and Lq.

`Stator q-axis inductance, Lq` — Q-составляющая-индукции статора
0.00022 `H` (значение по умолчанию)

Q-составляющая-индукции.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Constant Ld and Lq.

`Direct-axis current vector, iD` — Прямая ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию)

Прямая ось текущий вектор, ID.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld and Lq.

`Quadrature-axis current vector, iQ` — Квадратурная ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию)

Квадратурная ось текущий вектор, IQ.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld and Lq.

`Ld matrix, Ld(id,iq)` — Матрица Ld
`0.00022 * ones(3, 3)` `H` (значение по умолчанию)

Матрица Ld.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld and Lq.

`Lq matrix, Lq(id,iq)` — Матрица Lq
`0.00022 * ones(3, 3)` `H` (значение по умолчанию)

Матрица Lq.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld and Lq.

`Stator zero-sequence inductance, L0` — Индуктивность нулевой последовательности статора
0.00016 `H` (значение по умолчанию)

Индуктивность нулевой последовательности.

Зависимости

Включить этот параметр также:

Установите Winding Type на Wye-wound, Zero sequence к Include, и Stator parameterization к Specify Ld, Lq, and L0.
Установите Winding Type на Delta-wound и Stator parameterization к Specify Ld, Lq, and L0.

`Stator self-inductance per phase, Ls` — Самоиндукция статора на фазу
0.0002 `H` (значение по умолчанию)

Средняя самоиндукция каждой из трех обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ls, Lm, and Ms.

`Stator inductance fluctuation, Lm` — Колебание индуктивности статора
0 `H` (значение по умолчанию)

Колебание самоиндукции и взаимной индуктивности обмоток статора с углом ротора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ls, Lm, and Ms.

`Stator mutual inductance, Ms` — Статор взаимная индуктивность
0.00002 `H` (значение по умолчанию)

Средняя взаимная индуктивность между обмотками статора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ls, Lm, and Ms.

`Stator resistance per phase, Rs` — Сопротивление статора на фазу
0.013 `Ohm` (значение по умолчанию)

Сопротивление каждой из обмоток статора.

`Zero sequence` — Нулевая опция последовательности
`Include` (значение по умолчанию) | `Exclude`

Опция, чтобы включать или исключить термины нулевой последовательности.

Include — Включайте термины нулевой последовательности. Чтобы приоритизировать точность модели, используйте эту настройку по умолчанию. Используя эту опцию:
- Результаты по ошибке для симуляций, которые используют решатель Разделения. Для получения дополнительной информации смотрите, что Скорость симуляции Увеличения Использует Решатель Разделения.
- Отсоединяет параметр нулевой последовательности в настройках Impedances.
Exclude — Исключите термины нулевой последовательности. Чтобы приоритизировать скорость симуляции для настольной симуляции или развертывания приложений, выберите эту опцию.

Зависимости

Этот параметр отображается только, когда вы устанавливаете параметр Winding Type на Wye-wound.

Потери в железе

`Iron-loss` — Включите расчет Потерь в железе
`None` (значение по умолчанию) | `Empirical`

Задайте вычислительную модель потерь в железе.

`Open-circuit iron losses, [P_hysteresis P_eddy P_excess]` — Потери в железе разомкнутой цепи
[0, 0, 0] `W` (значение по умолчанию)

Вектор-строка, длины 3, потерь в железе разомкнутой цепи из-за гистерезиса, Эдди и избыточных потерь, соответственно, на частоте задан Electrical frequency at which losses determined.

Зависимости

Чтобы включить этот параметр, установите Iron-loss на Empirical.

`Short-circuit iron losses, [P_hysteresis P_eddy P_excess]` — Потери в железе короткой схемы
[0, 0, 0] `W` (значение по умолчанию)

Вектор-строка, длины 3, потерь в железе короткой схемы из-за гистерезиса, Эдди и избыточных потерь, соответственно, на частоте задан Electrical frequency at which losses determined.

Зависимости

Чтобы включить этот параметр, установите Iron-loss на Empirical.

`Electrical frequency at which losses determined` — Электрическая частота, на которой определяются потери
60 `Hz` (значение по умолчанию)

Электрическая частота, на которой были измерены разомкнутая цепь и потери в железе короткой схемы.

Зависимости

Чтобы включить этот параметр, установите Iron-loss на Empirical.

`Short-circuit RMS current for short-circuit iron losses` — RMS короткой схемы, текущая для потерь в железе короткой схемы
95 `A` (значение по умолчанию)

Получившаяся фаза RMS короткой схемы, текущая при измерении потерь короткой схемы.

Зависимости

Чтобы включить этот параметр, установите Iron-loss на Empirical.

Механическое устройство

`Rotor inertia` — Инерция ротора
0.01 `kg*m^2` (значение по умолчанию)

Инерция ротора присоединяется к механическому поступательному порту R. Значение может быть нулем.

`Rotor damping` — Затухание ротора
0 `N*m/(rad/s)` (значение по умолчанию)

Ротационное затухание.

Температурная зависимость

Эти параметры появляются только для блоков с осушенными тепловыми портами. Для получения дополнительной информации смотрите Тепловые Порты.

`Measurement temperature` — Температура измерения
298.15 `K` (значение по умолчанию)

Температура, для которой заключаются в кавычки параметры двигателя.

`Resistance temperature coefficient` — Коэффициент температуры сопротивления
`3.93e-3` `1/K` (значение по умолчанию)

Коэффициент α в сопротивлении связи уравнения температуре, как описано в Тепловой Модели для Блоков Привода. Значение по умолчанию для меди.

`Permanent magnet flux temperature coefficient` — Коэффициент температуры потока постоянного магнита
-0.001 `1/K` (значение по умолчанию)

Дробная скорость изменения плотности потока постоянного магнита с температурой. Это используется, чтобы линейно уменьшать крутящий момент и вызванный коэффициент противо-ЭДС, когда температура повышается.

Тепловой порт

`Thermal mass for each stator winding` — Количество тепла для каждой обмотки статора
100 `J/K` (значение по умолчанию)

Значение количества тепла для A, B, и обмотки C. Количество тепла является энергией, требуемой для повышения температуры на один градус.

`Rotor thermal mass` — Количество тепла ротора
200 `J/K` (значение по умолчанию)

Количество тепла ротора, то есть, энергия, требуемая повысить температуру ротора одной степенью.

`Percentage of main flux path iron losses associated with the rotor` — Процент основных потерь в железе пути к потоку сопоставлен с ротором
90 (значение по умолчанию)

Процент основных потерь в железе пути к потоку сопоставлен с магнитным путем через ротор. Это определяет, сколько из нагревания потери в железе приписано ротору тепловой порт HR, и сколько приписано трем извилистым тепловым портам HA, HB и HC.

Зависимости

Чтобы включить этот параметр, установите Iron-loss на Empirical.

`Percentage of cross-tooth flux path iron losses associated with the rotor` — Процент перекрестных зубных потерь в железе пути к потоку сопоставлен с ротором
30 (значение по умолчанию)

Процент перекрестных зубных потерь в железе пути к потоку сопоставлен с магнитным путем через ротор. Это определяет, сколько из нагревания потери в железе приписано ротору тепловой порт HR, и сколько приписано трем извилистым тепловым портам HA, HB и HC.

Зависимости

Чтобы включить этот параметр, установите Iron-loss на Empirical.

Примеры модели

Регулировка скорости BLDC

Контролируйте скорость ротора в базирующемся электрическом диске BLDC. Идеальный источник крутящего момента обеспечивает загрузку. Подсистема Управления использует основанную на PI структуру каскадного регулирования с внешним циклом регулировки скорости и внутренним циклом управления напряжения dc-ссылки. Напряжение dc-ссылки настроено через понижающий конвертер DC-DC. BLDC питается управляемым трехфазным инвертором. Сигналы логического элемента для инвертора получены из сигналов Холла. Симуляция использует шаги скорости. Подсистема Осциллографов содержит осциллографы, которые позволяют вам видеть результаты симуляции.

BLDC Position Control with Thermal Model

Управление положением BLDC с тепловой моделью

Управляйте углом ротора в базирующемся электрическом диске BLDC. BLDC включает тепловые и эмпирические потери в железе модели. Идеальный источник крутящего момента обеспечивает загрузку. Подсистема Управления использует основанную на PI структуру каскадного регулирования с тремя циклами управления: внешний цикл управления положения, цикл регулировки скорости и внутренний текущий цикл управления. BLDC питается управляемым трехфазным инвертором. Сигналы логического элемента для инвертора получены из сигналов Холла. Симуляция использует ссылки шага. Начальная температура обмоток статора и ротора установлена в 25 градусов Цельсия. Температура окружающей среды составляет 27 градусов Цельсия. Подсистема Осциллографов содержит осциллографы, которые позволяют вам видеть результаты симуляции.

Вопросы совместимости

развернуть все

Обновление портов электрического соединения

Поведение изменяется в R2021b

От R2021b вперед, чтобы переключиться между составным объектом и расширенными портами, устанавливают параметр Electrical connection на любой Composite three-phase ports или Expanded three-phase ports.

Ссылки

[1] Kundur, P. Устойчивость энергосистемы и управление. Нью-Йорк, Нью-Йорк: Макгроу Хилл, 1993.

[2] Андерсон, пополудни анализ неработающих энергосистем. Хобокен, NJ: нажатие Wiley-IEEE, 1995.

[3] Меллор, P.H., Р. Робель и Д. Холидей. “В вычислительном отношении эффективная модель потери в железе для бесщеточных машин AC, которая обслуживает расчетный поток и поле, ослабила операцию”. IEEE Электрическая Конференция по Машинам и Дискам. Май 2009.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Блоки Simscape

Permanent Magnet Synchronous Motor | Hybrid Excitation Synchronous Machine

Блоки

BLDC Commutation Logic | BLDC Current Controller with PWM Generation | BLDC Current Controller

Темы

Введенный в R2013b

Документация

BLDC

Описание

Моторная конструкция

Трапециевидная скорость изменения потока

Электрические уравнения определения

Упрощенные уравнения

Вычисление потерь в железе

Предопределенная параметризация

Тепловые порты

Переменные

Порты

Сохранение

~ — Трехфазный порт электрический

Зависимости

a — a - фаза электрический

Зависимости

b — b - фаза электрический

Зависимости

c — c - фаза электрический

Зависимости

n — Нейтральная фаза электрический

Зависимости

R — Моторный ротор механическое устройство

C — Моторный случай механическое устройство

HA — Обмотка теплового порта тепловой

HB — Обмотка B тепловой порт тепловой

HC — Обмотка C тепловой порт тепловой

HR — Ротор тепловой порт тепловой

Параметры

Ротор

Electrical connection — Электрическое соединение Composite three-phase ports (значение по умолчанию) | Expanded three-phase ports

Winding type — Настройка обмоток Wye-wound (значение по умолчанию) | Delta-wound

Maximum permanent magnet flux linkage — Максимальное потокосцепление постоянного магнита0.03 Wb (значение по умолчанию)

Зависимости

Rotor angle over which back emf is constant — Угол ротора, по которому коэффициент противо-ЭДС является постоянным pi / 12 rad (значение по умолчанию)

Зависимости

Maximum rotor-induced back emf — Максимум вызванный ротором коэффициент противо-ЭДС9.6 V (значение по умолчанию)

Зависимости

Rotor-induced back emf — Вызванный ротором коэффициент противо-ЭДС[0, -9.6, -9.6, 9.6, 9.6, 0] V (значение по умолчанию)

Зависимости

Flux linkage partial derivative with respect to rotor angle — Частная производная потокосцепления относительно угла ротора[0, -.1528, -.1528, .1528, .1528, 0] Wb/rad (значение по умолчанию)

Corresponding rotor angles — Соответствующие углы ротора[0, 7.5, 22.5, 37.5, 52.5, 60] deg (значение по умолчанию)

Зависимости

Rotor speed used for back emf measurement — Скорость ротора используется для измерения коэффициента противо-ЭДС600 rpm (значение по умолчанию)

Зависимости

Number of pole pairs Количество пар полюсов6 (значение по умолчанию)

Rotor angle definition — Контрольная точка для углового измерения ротора Angle between the a-phase magnetic axis and the d-axis (значение по умолчанию) | Angle between the a-phase magnetic axis and the q-axis

Статор

Modeling fidelity — Моделирование точности Constant Ld and Lq (значение по умолчанию) | Tabulated Ld and Lq

Зависимости

Stator parameterization — Параметризация статора Specify Ld, Lq, and L0 (значение по умолчанию) | Specify Ls, Lm, and Ms

Stator d-axis inductance, Ld — D-составляющая-индукции статора0.00022 H (значение по умолчанию)

Зависимости

Stator q-axis inductance, Lq — Q-составляющая-индукции статора0.00022 H (значение по умолчанию)

Зависимости

Direct-axis current vector, iD — Прямая ось текущий вектор[-200, 0, 200] A (значение по умолчанию)

Зависимости

Quadrature-axis current vector, iQ — Квадратурная ось текущий вектор[-200, 0, 200] A (значение по умолчанию)

Зависимости

Ld matrix, Ld(id,iq) — Матрица Ld 0.00022 * ones(3, 3) H (значение по умолчанию)

Зависимости

Lq matrix, Lq(id,iq) — Матрица Lq 0.00022 * ones(3, 3) H (значение по умолчанию)

Зависимости

Stator zero-sequence inductance, L0 — Индуктивность нулевой последовательности статора0.00016 H (значение по умолчанию)

Зависимости

Stator self-inductance per phase, Ls — Самоиндукция статора на фазу0.0002 H (значение по умолчанию)

Зависимости

Stator inductance fluctuation, Lm — Колебание индуктивности статора0 H (значение по умолчанию)

Зависимости

Stator mutual inductance, Ms — Статор взаимная индуктивность0.00002 H (значение по умолчанию)

Зависимости

Stator resistance per phase, Rs — Сопротивление статора на фазу0.013 Ohm (значение по умолчанию)

Zero sequence — Нулевая опция последовательности Include (значение по умолчанию) | Exclude

Зависимости

Потери в железе

Iron-loss — Включите расчет Потерь в железе None (значение по умолчанию) | Empirical

Open-circuit iron losses, [P_hysteresis P_eddy P_excess] — Потери в железе разомкнутой цепи[0, 0, 0] W (значение по умолчанию)

Зависимости

Short-circuit iron losses, [P_hysteresis P_eddy P_excess] — Потери в железе короткой схемы[0, 0, 0] W (значение по умолчанию)

`~` — Трехфазный порт
электрический

`a` — a - фаза
электрический

`b` — b - фаза
электрический

`c` — c - фаза
электрический

`n` — Нейтральная фаза
электрический

`R` — Моторный ротор
механическое устройство

`C` — Моторный случай
механическое устройство

`HA` — Обмотка теплового порта
тепловой

`HB` — Обмотка B тепловой порт
тепловой

`HC` — Обмотка C тепловой порт
тепловой

`HR` — Ротор тепловой порт
тепловой

`Electrical connection` — Электрическое соединение
`Composite three-phase ports` (значение по умолчанию) | `Expanded three-phase ports`

`Winding type` — Настройка обмоток
`Wye-wound` (значение по умолчанию) | `Delta-wound`

`Maximum permanent magnet flux linkage` — Максимальное потокосцепление постоянного магнита
0.03 `Wb` (значение по умолчанию)

`Rotor angle over which back emf is constant` — Угол ротора, по которому коэффициент противо-ЭДС является постоянным
`pi / 12` `rad` (значение по умолчанию)

`Maximum rotor-induced back emf` — Максимум вызванный ротором коэффициент противо-ЭДС
9.6 `V` (значение по умолчанию)

`Rotor-induced back emf` — Вызванный ротором коэффициент противо-ЭДС
[0, -9.6, -9.6, 9.6, 9.6, 0] `V` (значение по умолчанию)

`Flux linkage partial derivative with respect to rotor angle` — Частная производная потокосцепления относительно угла ротора
[0, -.1528, -.1528, .1528, .1528, 0] `Wb/rad` (значение по умолчанию)

`Corresponding rotor angles` — Соответствующие углы ротора
[0, 7.5, 22.5, 37.5, 52.5, 60] `deg` (значение по умолчанию)

`Rotor speed used for back emf measurement` — Скорость ротора используется для измерения коэффициента противо-ЭДС
600 `rpm` (значение по умолчанию)

`Number of pole pairs` Количество пар полюсов
6 (значение по умолчанию)

`Rotor angle definition` — Контрольная точка для углового измерения ротора
`Angle between the a-phase magnetic axis and the d-axis` (значение по умолчанию) | `Angle between the a-phase magnetic axis and the q-axis`

`Modeling fidelity` — Моделирование точности
`Constant Ld and Lq` (значение по умолчанию) | `Tabulated Ld and Lq`

`Stator parameterization` — Параметризация статора
`Specify Ld, Lq, and L0` (значение по умолчанию) | `Specify Ls, Lm, and Ms`

`Stator d-axis inductance, Ld` — D-составляющая-индукции статора
0.00022 `H` (значение по умолчанию)

`Stator q-axis inductance, Lq` — Q-составляющая-индукции статора
0.00022 `H` (значение по умолчанию)

`Direct-axis current vector, iD` — Прямая ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию)

`Quadrature-axis current vector, iQ` — Квадратурная ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию)

`Ld matrix, Ld(id,iq)` — Матрица Ld
`0.00022 * ones(3, 3)` `H` (значение по умолчанию)

`Lq matrix, Lq(id,iq)` — Матрица Lq
`0.00022 * ones(3, 3)` `H` (значение по умолчанию)

`Stator zero-sequence inductance, L0` — Индуктивность нулевой последовательности статора
0.00016 `H` (значение по умолчанию)

`Stator self-inductance per phase, Ls` — Самоиндукция статора на фазу
0.0002 `H` (значение по умолчанию)

`Stator inductance fluctuation, Lm` — Колебание индуктивности статора
0 `H` (значение по умолчанию)

`Stator mutual inductance, Ms` — Статор взаимная индуктивность
0.00002 `H` (значение по умолчанию)

`Stator resistance per phase, Rs` — Сопротивление статора на фазу
0.013 `Ohm` (значение по умолчанию)

`Zero sequence` — Нулевая опция последовательности
`Include` (значение по умолчанию) | `Exclude`

`Iron-loss` — Включите расчет Потерь в железе
`None` (значение по умолчанию) | `Empirical`

`Open-circuit iron losses, [P_hysteresis P_eddy P_excess]` — Потери в железе разомкнутой цепи
[0, 0, 0] `W` (значение по умолчанию)

`Short-circuit iron losses, [P_hysteresis P_eddy P_excess]` — Потери в железе короткой схемы
[0, 0, 0] `W` (значение по умолчанию)

`Electrical frequency at which losses determined` — Электрическая частота, на которой определяются потери
60 `Hz` (значение по умолчанию)

`Short-circuit RMS current for short-circuit iron losses` — RMS короткой схемы, текущая для потерь в железе короткой схемы
95 `A` (значение по умолчанию)

`Rotor inertia` — Инерция ротора
0.01 `kg*m^2` (значение по умолчанию)

`Rotor damping` — Затухание ротора
0 `N*m/(rad/s)` (значение по умолчанию)

`Measurement temperature` — Температура измерения
298.15 `K` (значение по умолчанию)

`Resistance temperature coefficient` — Коэффициент температуры сопротивления
`3.93e-3` `1/K` (значение по умолчанию)

`Permanent magnet flux temperature coefficient` — Коэффициент температуры потока постоянного магнита
-0.001 `1/K` (значение по умолчанию)

`Thermal mass for each stator winding` — Количество тепла для каждой обмотки статора
100 `J/K` (значение по умолчанию)

`Rotor thermal mass` — Количество тепла ротора
200 `J/K` (значение по умолчанию)

`Percentage of main flux path iron losses associated with the rotor` — Процент основных потерь в железе пути к потоку сопоставлен с ротором
90 (значение по умолчанию)

`Percentage of cross-tooth flux path iron losses associated with the rotor` — Процент перекрестных зубных потерь в железе пути к потоку сопоставлен с ротором
30 (значение по умолчанию)

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.