Ожидаемый недостаток (ES) является ожидаемой потерей в дни, когда существует отказ Подверженного риску значения (VaR). Если VaR является 10 миллионами, и ES является 12 миллионами, мы знаем ожидаемую потерю завтра; если это, оказывается, очень плохой день, это на 20% выше, чем VaR. ES иногда называется Подверженным риску значения условным выражением (CVaR), Подверженным риску значения хвостом (TVaR), Условным ожиданием хвоста (TCE) или Условным ожиданием хвоста (CTE).
Существует много подходов к оценке VaR и ES, и они могут привести к различному VaR и оценкам ES. Как можно определить, оценивают ли модели точно риск ежедневно? Как можно оценить, который модель выполняет лучше? varbacktest инструменты помогают подтвердить эффективность моделей VaR относительно предполагаемых значений VaR. esbacktest, esbacktestbysim, и esbacktestbyde инструменты расширяют эти возможности оценить модели VaR относительно предполагаемых значений ES.
Для VaR backtesting возможности каждый день равняются двум: или существует отказ VaR или нет. Если доверительный уровень VaR составляет 95%, отказы VaR должны произойти приблизительно 5% времени. К backtest VaR только необходимо знать, был ли VaR превышен (отказ VaR) или не в каждый день тестового окна и доверительного уровня VaR. Инструменты VaR backtesting Risk Management Toolbox™ поддерживают “частоту” (оцените пропорцию отказов), и “независимость” (оценивают независимость через время) тесты и эти тесты работает с двоичной последовательностью результатов "отказа" или "безотказности" по тестовому окну.
Для ожидаемого недостатка (ES) возможности каждый день бесконечны: VaR может быть превышен на 1%, или на 10%, или на 150%, и так далее. Например, существует три отказа VaR в следующем примере:
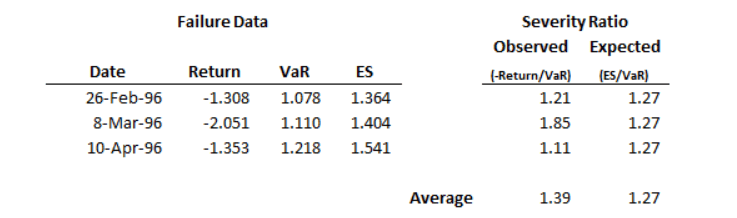
В дни отказа VaR превышен в среднем на 39%, но предполагаемый ES превышает VaR в среднем на 27%. Как можно сказать, значительно больше ли 39%, чем 27%? Знание доверительного уровня VaR недостаточно, необходимо ли также знать, с какой вероятностью различные exceedances по VaR согласно модели VaR. Другими словами, вам нужна некоторая информация о распределении о том, что происходит вне VaR согласно вашим предположениям модели. Для моделей VaR тонкого хвоста 39% по сравнению с 27% могут быть значительными различиями. Однако для модели VaR тяжелого хвоста, где серьезность дважды VaR имеет нетривиальную вероятность случая, затем 39% по сравнению с 27% по трем датам отказа не могут быть красным флагом.
Основное отличие между VaR backtesting и ES backtesting - то, что большая часть ES backtesting методы запрашивает информацию о распределении возвратов в каждый день, или по крайней мере распределении хвостов вне VaR. Одним исключением является “безусловный” тест (см. unconditionalNormal и unconditionalT) где можно получить аппроксимированные результаты испытаний, не предоставляя информацию о распределении. Это важно на практике, потому что “безусловный” тест намного более прост использовать и может использоваться в принципе для любой модели VaR или ES. Компромисс - то, что аппроксимированные результаты могут быть неточными, особенно в границе принимают или отклоняют дела, или для определенных типов распределений.
Тулбокс поддерживает следующие тесты для ожидаемого недостатка backtesting для основанных на таблице тестов для безусловного теста Acerbi-Szekely с помощью esbacktest объект:
ES backtests обязательно аппроксимирован в этом, они чувствительны к ошибкам в предсказанном VaR. Однако минимально смещенный тест имеет только маленькую чувствительность к ошибкам VaR, и чувствительность является благоразумной, в том смысле, что ошибки VaR приводят к более карательному тесту ES. См. Acerbi-Szekely (2017 и 2019) для деталей. Когда информация о распределении доступна, минимально смещенный тест (minBiasRelative или minBiasAbsolute) рекомендуется.
Тулбокс поддерживает следующие основанные на симуляции тесты Acerbi-Szekely для ожидаемого недостатка backtesting использование esbacktestbysim объект:
Для основанных на симуляции тестов Acerbi-Szekely необходимо предоставить информацию о распределении модели как часть входных параметров к esbacktestbysim.
Тулбокс также поддерживает следующие тесты Du и Escanciano для ожидаемого недостатка backtesting использование esbacktestbyde объект:
Для Du и Escanciano основанные на симуляции тесты, необходимо предоставить информацию о распределении модели как часть входных параметров к esbacktestbyde.
Тестовая статистическая величина conditional Acerbi и Szekely основана на условном отношении
где
Xt является результатом портфеля, то есть, портфель возвращаются или прибыль портфеля и потеря в течение периода t.
VaRt является предполагаемый VaR в течение периода t.
ESt является предполагаемым ожидаемым недостатком в течение периода t.
Количество отказов задано как
где
N количество периодов в тестовом окне (t = 1N).
It является индикатором отказа VaR на периоде t со значением 1 если Xt <-var, и 0 в противном случае.
Условная тестовая статистическая величина задана как
Условный тест имеет две части. VaR backtest должен быть запущен для количества отказов (NumFailures), и автономный условный тест выполняется для условной тестовой статистической величины Zcond. Условный тест принимает модель только, когда и тест VaR и автономный условный тест принимают модель. Для получения дополнительной информации смотрите conditional.
Тестовая статистическая величина unconditional Acerbi и Szekely основана на безусловном отношении,
где
Xt является результатом портфеля, то есть, портфель возвращаются или прибыль портфеля и потеря в течение периода t.
PVaR является вероятностью отказа VaR, заданного как уровень с 1 var.
ESt является предполагаемым ожидаемым недостатком в течение периода t.
It является индикатором отказа VaR на периоде t со значением 1 если Xt <-var, и 0 в противном случае.
Безусловная тестовая статистическая величина задана как
Критические значения для безусловной тестовой статистической величины устойчивы через область значений распределений, которая является базисом для основанных на таблице тестов. esbacktest класс запускает безусловный тест против предварительно вычисленных критических значений под двумя дистрибутивными предположениями, а именно, нормальное распределение (тонкие хвосты, смотрите unconditionalNormal), и распределение t с 3 степенями свободы (тяжелые хвосты, смотрите unconditionalT).
Демонстрационное средство оценки ожидаемого недостатка для демонстрационного Y1, …, YN:
где
N количество периодов в тестовом окне (t = 1N).
PVaR является вероятностью отказа VaR, заданного как уровень с 1 var.
Y1, …, YN являются отсортированными демонстрационными значениями (от самого маленького до самого большого), и самое большое целое число, меньше чем или равное NpVar.
Чтобы вычислить квантиль тестируют статистическую величину, выборку размера N создается в каждый раз t можно следующим образом. Во-первых, преобразуйте результаты портфеля в Xt к рангам использование кумулятивной функции распределения Pt. Если предположения распределения правильны, значения ранга U1, …, UN равномерно распределены в интервале (0,1). Затем в каждый раз t:
Инвертируйте ранги U = (U1, …, UN) получить N квантили .
Вычислите демонстрационное средство оценки .
Вычислите ожидаемое значение демонстрационного средства оценки
где V = (V1, …, VN) выборка N независимые универсальные случайные переменные в интервале (0,1). Это может быть вычислено аналитически.
Тестовая статистическая величина квантиля Acerbi и Szekely задана как
Знаменатель в сумме может быть вычислен аналитически как
где Ix (zW) упорядоченная неполная бета-функция. Для получения дополнительной информации смотрите betainc и quantile.
Минимально смещенная тестовая статистическая величина Acerbi и Szekely основана на следующем представлении VaR и ES (см. Acerbi и Szekely 2017 и 2019 для деталей и также Рокэфеллэра и Урясева 2002, и Acerbi и Tasche 2002):
где
X является результатом портфеля.
(x) _ является отрицательной функцией, определяемой части как (x) _ = макс. (0,-x).
ɑ уровень с 1 var.
Тестовая статистическая величина имеет абсолютную версию и относительную версию. Абсолютной версией минимально смещенной тестовой статистической величины дают
где
X t является результатом портфеля, который является портфелем, возвращается или прибыль портфеля и потеря в течение периода t.
VaR t является существенный VaR в течение периода t.
ES t является ожидаемым недостатком в течение периода t.
p VaR является вероятностью Отказа Var, заданного как уровень с 1 var.
N является количеством периодов в тестовом окне (t = 1... N).
(x) _ отрицательная функция, определяемая части как (x) _ = макс. (0,-x).
Относительной версией минимально смещенной тестовой статистической величины дают
ES backtests обязательно аппроксимирован в этом, они чувствительны к ошибкам в предсказанном VaR. Однако минимально смещенный тест имеет только маленькую чувствительность к ошибкам VaR, и чувствительность является благоразумной, в том смысле, что ошибки VaR приводят к более карательному тесту ES. См. Acerbi-Szekely (2017 и 2019) для деталей. Когда информация о распределении доступна, минимально смещенный тест рекомендуется. Для получения дополнительной информации смотрите minBiasRelative и minBiasAbsolute.
В течение каждого дня модель Дю-Эсканкяно принимает распределение для возвратов. Например, если у вас есть нормальное распределение с условным отклонением 1,5%, существует соответствующая кумулятивная функция распределения P t. Путем отображения возвратов X t с распределением P t вы становитесь “сопоставленными, возвращает” серию U t, также известную как ряд "рангов", который конструкцией имеет значения между 0 и 1 (см. столбец 2 в следующей таблице). Позвольте α быть дополнением уровня VaR — например, если уровень VaR составляет 95%, α составляет 5%. Если сопоставленный возврат U, t меньше, чем α, то существует VaR “нарушение” или VaR “отказ”. Это эквивалентно наблюдению возврата X t, меньший, чем отрицание значения VaR в течение того дня, с тех пор, конструкцией, отрицание значения VaR сопоставлено с α. Поэтому можно сравнить U t с α, даже не зная значения VaR. Ряд отказов VaR обозначается h t, и это - серия 0 и 1's сохраненный в столбце 3 в следующей таблице. Наконец, столбец 4 в следующей таблице содержит “совокупные нарушения” ряд, обозначенный H t. Это - серьезность сопоставленных нарушений VaR в дни, в которые нарушен VaR. Например, если сопоставленный возврат, U, t составляет 1% и α, составляет 5%, H t, составляет 4%. H t задан как нуль, при отсутствии нарушений VaR.
| Xt | U t = P t (X t) | h t = U t <α | H t = (α - U t) * h t |
|---|---|---|---|
| 0.00208 | 0.5799 | 0 | 0 |
| -0.01073 | 0.1554 | 0 | 0 |
| -0.00825 | 0.2159 | 0 | 0 |
| -0.02967 | 0.0073 | 1 | 0.0427 |
| 0.01242 | 0.8745 | 0 | 0 |
| ... | ... | ... | ... |
Учитывая серию h t нарушений и совокупную серию H t нарушений, тесты Дю-Эсканкяно (DE) получены в итоге как:
| Тест Дю-Эсканкяно | Тест VaR | Тест ES |
|---|---|---|
| Безусловный | Среднее значение h t | Среднее значение H t |
| Условное выражение | Автокорреляция h t | Автокорреляция H t |
Тесты DE VaR оценивают среднее значение и автокорреляцию серии h t и получившееся тестовое перекрытие с известными тестами VaR. Например, среднее значение h t, как ожидают, будет совпадать с α. Другими словами, пропорция времени, VaR нарушен, как ожидают, будет совпадать с доверительным уровнем. Этот тест поддерживается в varbacktest класс с пропорцией отказов (pof) тест (конечная выборка) и бином (bin) тест (приближение большой выборки). В свою очередь условные VaR тестируют меры, если существует шаблон времени в последовательности отказов VaR (компенсационные отказы, и так далее). Условная независимость покрытия (cci) протестируйте в varbacktest класс тестирует на независимость с одной задержкой. Время между независимостью отказов (tbfi) протестируйте в varbacktest класс также оценивает независимость времени для моделей VaR.
esbacktestbyde класс поддерживает тесты ES DE. Тесты ES DE оценивают среднее значение и автокорреляцию серии H t. Для безусловного теста (unconditionalDE), ожидаемое значение является α/2 — например, среднее значение в нижней части 5% универсальной формы (0,1), распределение составляет 2,5%. Условный тест (conditionalDE) оценивает, не только если отказ происходит, но также и если серьезность отказа коррелируется к предыдущим возникновениям отказа и их строгому обращению.
Тестовая статистическая величина для безусловного теста ES DE
Если количество наблюдений является большим, тестовая статистическая величина распределяется как
где N (μ,σ2) нормальное распределение со средним значением μ и отклонение σ2.
Безусловный тест ES DE является двухсторонним тестом, который проверяет, ли тестовая статистическая величина близко к ожидаемому значению α/2. От ограничивающего распределения выведен доверительный уровень. Конечно-демонстрационные доверительные интервалы оцениваются посредством симуляции.
Тестовая статистическая величина для условного теста ES DE выведена на нескольких шагах. Во-первых, задайте автоковариацию для задержки j:
Автокорреляция для задержки j затем
Тестовая статистическая величина для задержек m затем
Если количество наблюдений является большим, тестовая статистическая величина распределяется как распределение хи-квадрат со степенями свободы m:
Условный тест ES DE является односторонним тестом, чтобы определить, намного больше ли условная тестовая статистическая величина ES DE, чем нуль. Если так, существует доказательство автокорреляции. Ограничивающее распределение вычисляет критические значения большой выборки. Конечно-демонстрационные критические значения оцениваются посредством симуляции.
backtesting инструменты, поддержанные Risk Management Toolbox, имеют следующие требования и функции.
| Инструмент Backtesting | PortfolioData Необходимый | VarData Необходимый | ESData Необходимый | VaRLevel Необходимый[a] | PortfolioID и VaRID Поддерживаемый | Distribution Необходимая информация | Многоуровневые модели поддержек[b] | Поддержки несколько VaRLevels |
|---|---|---|---|---|---|---|---|---|
varbacktest | Да | Да | Нет | Да | Да | Нет | Да | Да |
esbacktest | Да | Да | Да | Да | Да | Нет | Да | Да |
esbacktestbysim | Да | Да | Да | Да | Да | Да | Нет | Да |
esbacktestbyde | Да | Нет | Нет | Да | Да | Да | Нет | Да |
[a] [b] Например, вы можете backtest | ||||||||
Risk Management Toolbox поддерживает следующие backtesting инструменты и их связанные тесты.
| Протестируйте тип | Протестируйте имя | Тесты для | Рискните мерой | Расчет критического значения | Используйте объект | Используйте функцию |
|---|---|---|---|---|---|---|
| Базель | Светофор | Частота | Var | Точная конечная выборка (бином) | varbacktest | tl |
| Различный | Бином | Частота | Var | Большая выборка нормальное приближение | varbacktest | bin |
| Kupiec | Пропорция отказов | Частота | Var | Точная конечная выборка (регистрируют вероятность), | varbacktest | pof |
| Kupiec | Время до первого отказа | Независимость | Var | Точная конечная выборка (регистрируют вероятность), | varbacktest | tuff |
| Кристофферсен | Условное покрытие, смешанное | Частота и независимость | Var | Точная конечная выборка (регистрируют вероятность), | varbacktest | cc |
| Кристофферсен | Условное покрытие, независимость | Независимость | Var | Точная конечная выборка (регистрируют вероятность), | varbacktest | cci |
| Хаас | Смешанный тест Kupiec | Частота и независимость | Var | Точная конечная выборка (регистрируют вероятность), | varbacktest | tbf |
| Хаас | Независимость (время между отказами) | Независимость | Var | Точная конечная выборка (регистрируют вероятность), | varbacktest | tbfi |
| Acerbi-Szekely | "Протестируйте 2" или безусловный | Серьезность | ES | Таблицы предварительно симулированных критических значений, под нормальным и распределением t | esbacktest | unconditionalNormal и unconditionalT |
| Acerbi-Szekely | "Протестируйте 1" или условное выражение | Серьезность | ES | Конечно-демонстрационная симуляция | esbacktestbysim | conditional |
| Acerbi-Szekely | "Протестируйте 2" или безусловный | Серьезность | ES | Конечно-демонстрационная симуляция | esbacktestbysim | unconditional |
| Acerbi-Szekely | "Протестируйте 1" или ранги (квантиль) | Серьезность | ES | Конечно-демонстрационная симуляция | esbacktestbysim | quantile |
| Acerbi-Szekely | Минимально Смещенная, относительная версия | Серьезность | ES | Конечно-демонстрационная симуляция | esbacktestbysim | minBiasRelative |
| Acerbi-Szekely | Минимально Смещенная, абсолютная версия | Серьезность | ES | Конечно-демонстрационная симуляция | esbacktestbysim | minBiasAbsolute |
| Дю-Эсканкяно | Безусловный | Серьезность | ES | Приближение большой выборки и конечно-демонстрационная симуляция | esbacktestbyde | unconditionalDE |
| Дю-Эсканкяно | Условное выражение | Независимость | ES | Приближение большой выборки и конечно-демонстрационная симуляция | esbacktestbyde | conditionalDE |
[1] Базельский Комитет по Банковскому надзору. Контрольная Среда для Использования “Backtesting” в сочетании с Внутренним Подходом Моделей к Требованиям Рискового капитала Рынка. Январь 1996. https://www.bis.org/publ/bcbs22.htm.
[2] Acerbi, C. и Б. Сзекели. Бэктестинг ожидаемый недостаток. Декабрь 2014 MSCI Inc.
[3] Acerbi, C. и Б. Сзекели. "Общие свойства статистики Backtestable. SSRN электронный журнал. Январь 2017.
[4] Acerbi, C. и Б. Сзекели. "Минимально смещенный Backtest для ES". Риск. Сентябрь 2019.
[5] Acerbi, C. и Д. Тэш. “На Когерентности Ожидаемого Недостатка”. Журнал Банковского дела и Финансов. Издание 26, 2002, стр 1487-1503.
[6] Du, Z. и Х. К. Эскансиано. "Бэктестинг ожидаемый недостаток: составление риска хвоста". Наука управления. Издание 63, выпуск 4, апрель 2017.
[7] Rockafellar, R. T. и С. Урясев. "Условное выражение, Подверженное риску значения Общих Распределений Потерь". Журнал Банковского дела и Финансов. Издание 26, 2002, стр 1443-1471.
esbacktestbyde | esbacktest | esbacktestbysim | varbacktest