Интерпретация H-нормы-по-бесконечности

Нормы сигналов и систем

Существует несколько способов задать нормы скалярного сигнала e (t) во временном интервале. Мы будем часто использовать 2-норму, (_2-норма L), для математического удобства, которое задано как

${‖ e ‖}_{2} : = {(\int_{- \infty}^{\infty} e {(t)}^{2} d t)}^{\frac{1}{2}} .$

Если этот интеграл конечен, то сигнал e интегрируем с квадратом, обозначен как e ∊ L2. Для сигналов с векторным знаком

$e (t) = [\begin{matrix} e_{1} (t) \\ e_{2} (t) \\ ⋮ \\ e_{n} (t) \end{matrix}],$

2-норма задана как

$\begin{matrix} {‖ e ‖}_{2} : = {(\int_{- \infty}^{\infty} {‖ e (t) ‖}_{2}^{2} d t)}^{\frac{1}{2}} \\ = {(\int_{- \infty}^{\infty} e^{T} (t) e (t) d t)}^{\frac{1}{2}} . \end{matrix}$

В µ-tools динамические системы, с которыми мы имеем дело, исключительно линейны с моделью в пространстве состояний

$[\begin{matrix} \dot{x} \\ e \end{matrix}] = [\begin{matrix} A & B \\ C & D \end{matrix}] [\begin{matrix} x \\ d \end{matrix}],$

или, в форме передаточной функции,

e (s) = T (s) d (s), T (s): = C (СИ – A)^–1B + D

Двумя математически удобными мерами матрицы T (s) передачи в частотном диапазоне является матричный _H2 и H _∞ нормы,

$\begin{array}{l} {‖ T ‖}_{2} : = {[\frac{1}{2 π} \int_{- \infty}^{\infty} {‖ T (j ω) ‖}_{F}^{2} d ω]}^{\frac{1}{2}} \\ {‖ T ‖}_{\infty} : = \underset{ω \in R}{\max \bar{σ}} [T (j ω)], \end{array}$

где норма Фробениуса (см. MATLAB^® norm команда) комплексной матрицы M

${‖ M ‖}_{F} : = \sqrt{Trace (M^{*} M)} .$

Обе из этих норм передаточной функции имеют интерпретации временного интервала ввода/вывода. Если, начинающий с начального условия x (0) = 0, два сигнала d и e связаны

$[\begin{matrix} \dot{x} \\ e \end{matrix}] = [\begin{matrix} A & B \\ C & D \end{matrix}] [\begin{matrix} x \\ d \end{matrix}],$

то

Для d, модульной интенсивности, процесса белого шума, установившееся отклонение e является ∥T∥2.
L ₂ (или RMS) получает от d → e,
$\max_{d \neq 0} \frac{{‖ e ‖}_{2}}{{‖ d ‖}_{2}}$
равно ∥T _∥∞. Это обсуждено более подробно в следующем разделе.

Используя взвешенные нормы, чтобы охарактеризовать эффективность

Любой критерий производительности должен также составлять

Относительная величина внешних влияний
Зависимость частоты сигналов
Относительная важность величин отрегулированных переменных

Так, если цель эффективности в форме матричной нормы, это должна на самом деле быть взвешенная норма

_∥WLTWR ∥

где матрицы функции взвешивания _WL и _WR являются зависимым частоты, с учетом ограничений полосы пропускания и спектрального содержимого внешних сигналов. Самый естественный (математический) способ, чтобы охарактеризовать приемлемую эффективность в терминах MIMO ∥ · _∥∞ (H _∞) норма. Поэтому этот раздел теперь обсуждает некоторые интерпретации H _∞ норма.

Невзвешенная система MIMO

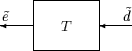
Предположим, что T является MIMO устойчивая линейная система с матрицей T (s) передаточной функции. Для данного управления сигналом $\tilde{d} (t)$ Define $\tilde{e}$ как выход, как показано ниже.

Обратите внимание на то, что более традиционно написать схему в Невзвешенной Системе MIMO: Векторы слева направо стрелками, идущими слева направо как во Взвешенной Системе MIMO.

Невзвешенная система MIMO: векторы слева направо

Две схемы, показанные выше, представляют ту же самую систему. Мы предпочитаем писать эти блок-схемы стрелками, собирающимися справа налево быть сопоставимыми с составом оператора и матрицей.

Примите, что размерностями T является _{ne ×} _{без обозначения даты}. Позвольте β> 0 быть заданным как

$β : = {‖ T ‖}_{\infty} : = \underset{ω \in R}{\max \bar{σ} [T (j ω)]} .$

Теперь считайте ответ, начинающий с начального условия равным 0. В этом случае теорема Парсевэла дает это

$\frac{{‖ \tilde{e} ‖}_{2}}{{‖ \tilde{d} ‖}_{2}} = \frac{{[\int_{0}^{\infty} {\tilde{e}}^{T} (t) \tilde{e} (t) d t]}^{\frac{1}{2}}}{{[\int_{0}^{\infty} {\tilde{d}}^{T} (t) \tilde{d} (t) d t]}^{\frac{1}{2}}} \leq β .$

Кроме того, существуют определенные воздействия d что результат в отношении ${‖ \tilde{e} ‖}_{2} / {‖ \tilde{d} ‖}_{2}$ произвольно близко к β. Из-за этого ∥T _∥∞ упоминается как L ₂ (или RMS) усиление системы.

Как вы ожидали бы, синусоидальная, установившаяся интерпретация ∥T _∥∞ также возможна: Для любой частоты $\bar{ω} \in R$ , любой вектор из амплитуд $a \in R_{n_{d}}$ , и любой вектор из фаз $ϕ \in R^{n_{d}}$ , с ∥a∥2 ≤ 1, задайте сигнал времени

$\tilde{d} (t) = [\begin{matrix} a_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ a_{n_{d}} \sin (\bar{ω} t + ϕ_{n_{d}}) \end{matrix}] .$

При применении этого входа к системе T приводит к установившемуся ответу ${\tilde{e}}_{s s}$ из формы

${\tilde{e}}_{s s} (t) = [\begin{matrix} b_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ b_{n_{e}} \sin (\bar{ω} t + ϕ_{n_{e}}) \end{matrix}] .$

Вектор $b \in R^{n_{e}}$ удовлетворит ∥b∥2 ≤ β. Кроме того, β, как задано во Взвешенной Системе MIMO, является самым маленьким номером, таким образом, что это верно для каждого ∥a∥2 ≤ 1, $\bar{ω}$ , и ϕ.

Обратите внимание на то, что в этой интерпретации, векторы из синусоидальных ответов величины не взвешены, и измеренные в Евклидовой норме. Если реалистические многомерные цели эффективности состоят в том, чтобы быть представлены одним MIMO ∥ · цель _∥∞ на передаточной функции с обратной связью, дополнительные масштабирования необходимы. Поскольку много различных целей смешиваются в одну матрицу, и связанная стоимость является нормой матрицы, важно использовать зависимые частотой функции взвешивания, так, чтобы различные требования могли быть обоснованно объединены в одну функцию стоимости. Диагональные веса наиболее легко интерпретированы.

Рассмотрите схему Взвешенной Системы MIMO, наряду с Невзвешенной Системой MIMO: Векторы слева направо.

Примите, что _WL и _WR являются диагональными, устойчивыми матрицами передаточной функции с диагональными элементами, обозначенными _Ли и _Ри.

$W_{L} = [\begin{matrix} L_{1} & 0 & \dots & 0 \\ 0 & L_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & L_{n_{e}} \end{matrix}], W_{R} = [\begin{matrix} R_{1} & 0 & \dots & 0 \\ 0 & R_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & R_{n_{d}} \end{matrix}] .$

Взвешенная система MIMO

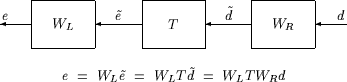
Границы на количестве _∥WLTWR _∥∞ будут подразумевать границы о синусоидальном установившемся поведении сигналов $\tilde{d}$ и $\tilde{e} (= T \tilde{d})$ в схеме Невзвешенной Системы MIMO: Векторы слева направо. А именно, для синусоидального сигнала $\tilde{d}$ , установившееся отношение между $\tilde{e} (= T \tilde{d})$ , $\tilde{d}$ и _∥WLTWR _∥∞ следующие. Установившееся решение ${\tilde{e}}_{s s}$ , обозначенный как

{\tilde{e}}_{s s} (t) = [\begin{matrix} {\tilde{e}}_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ {\tilde{e}}_{n_{e}} \sin (\bar{ω} t + ϕ_{n_{d}}) \end{matrix}]

(1)

удовлетворяет

$\sum_{i = 1}^{n_{e}} {| W_{L_{i}} (j \bar{ω}) {\tilde{e}}_{i} |}^{2} \leq 1$

для всех синусоидальных входных сигналов $\tilde{d}$ из формы

\tilde{d} (t) = [\begin{matrix} {\tilde{d}}_{1} \sin (\bar{ω} t + ϕ_{1}) \\ ⋮ \\ {\tilde{d}}_{n_{e}} \sin (\bar{ω} t + ϕ_{n_{d}}) \end{matrix}]

(2)

удовлетворение

$\sum_{i = 1}^{n_{d}} \frac{{| {\tilde{d}}_{i} |}^{2}}{{| W_{R_{i}} (j \bar{ω}) |}^{2}} \leq 1$

если и только если _∥WLTWR _∥∞ ≤ 1.

Это приблизительно (очень приблизительно — следующий оператор не на самом деле правилен) подразумевает что _∥WLTWR _∥∞ ≤ 1 если и только если для каждой фиксированной частоты $\bar{ω}$ , и все синусоидальные воздействия $\tilde{d}$ из удовлетворения уравнения 2 формы

$| {\tilde{d}}_{i} | \leq | W_{R_{i}} (j \bar{ω}) |$

установившиеся ошибочные компоненты удовлетворят

$| {\tilde{e}}_{i} | \leq \frac{1}{| W_{L_{i}} (j \bar{ω}) |} .$

Это показывает, как можно было выбрать веса эффективности, чтобы отразить желаемую зависимую частотой цель эффективности. Используйте _WR, чтобы представлять относительную величину воздействий синусоид, которые могут присутствовать, и использовать 1/_WL, чтобы представлять желаемую верхнюю границу при последующих ошибках, которые производятся.

Помните, однако, что взвешенный H _∞ норма на самом деле не дает поэлементно границы на компонентах $\tilde{e}$ на основе поэлементно ограничивает на компонентах $\tilde{d}$ . Точное связало его, дает, в терминах Евклидовых норм компонентов $\tilde{e}$ и $\tilde{d}$ (взвешенный соответственно _WL (j $\bar{ω}$ ) и _WR (j $\bar{ω}$ )).

Смотрите также

hinfstruct | hinfsyn

Документация