Exponenta Banner

loopsens

Функции чувствительности обратной связи контроллера объекта

свернуть все на странице

Синтаксис

loops = loopsens(P,C)

Описание

пример

loops = loopsens(P,C) вычисляет многомерную чувствительность, дополнительную чувствительность и передаточные функции разомкнутого контура системы с обратной связью, состоящей из контроллера C в отрицательной обратной связи с объектом P. Чтобы вычислить функции чувствительности для системы с положительной обратной связью, используйте loopsens(P,-C).

Примеры

свернуть все

Скрипт Open Live Script

Рассмотрите ПИ-контроллер для доминируя объекта первого порядка с полосой пропускания замкнутой системы 2,5 рад/секунда. Поскольку проблемой является SISO, все усиления являются тем же самым при вводе и выводе.

gamma = 2; tau = 1.5; taufast = 0.1; 
P = tf(gamma,[tau 1])*tf(1,[taufast 1]); 
tauclp = 0.4; 
xiclp = 0.8; 
wnclp = 1/(tauclp*xiclp); 
KP = (2*xiclp*wnclp*tau - 1)/gamma; 
KI = wnclp^2*tau/gamma; 
C = tf([KP KI],[1 0]);

Сформируйте с обратной связью (и разомкнутый контур) системы с loopsens, и постройте Диаграммы Боде функций чувствительности во входе объекта.

loops = loopsens(P,C); 
bode(loops.Si,'r',loops.Ti,'b',loops.Li,'g')
legend('Sensitivity','Complementary Sensitivity','Loop Transfer')

Figure contains 2 axes objects. Axes object 1 with title From: du To: Out(1) contains 3 objects of type line. These objects represent Sensitivity, Complementary Sensitivity, Loop Transfer. Axes object 2 contains 3 objects of type line. These objects represent Sensitivity, Complementary Sensitivity, Loop Transfer.

Наконец, сравните усиление объекта разомкнутого контура со значением с обратной связью PSi.

bodemag(P,'r',loops.PSi,'b')
legend('Plant','Sensitivity*Plant')

Figure contains an axes object. The axes object with title From: du To: yP contains 2 objects of type line. These objects represent Plant, Sensitivity*Plant.

Скрипт Open Live Script

Рассмотрите интегральный контроллер для постоянного усиления, объекта с 2 выходами, с 2 входами. В целях рисунка контроллер спроектирован через инверсию с различными полосами пропускания в каждом вращаемом канале.

P = ss([2 3;-1 1]); 
BW = diag([2 5]); 
[U,S,V] = svd(P.d);                % get SVD of Plant Gain 
Csvd = V*inv(S)*BW*tf(1,[1 0])*U'; % inversion based on SVD 
loops = loopsens(P,Csvd); 
bode(loops.So,'g',loops.To,'r',logspace(-1,3,120))
title('Output Sensitivity (green), Output Complementary Sensitivity (red)');

Figure contains 8 axes objects. Axes object 1 with title From: dy(1) contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 2 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 3 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 4 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 5 with title From: dy(2) contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 6 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 7 contains 2 objects of type line. These objects represent untitled1, untitled2. Axes object 8 contains 2 objects of type line. These objects represent untitled1, untitled2.

Входные параметры

свернуть все

Объект в виде модели динамической системы, блока системы управления или статической матрицы усиления. P может быть SISO или MIMO, настолько же долго как P*C имеет то же количество вводов и выводов.

P может быть непрерывное время или дискретное время. Если P обобщенная модель (такой как genss или ussто loopsens использует текущее значение или номинальную стоимость всех блоков системы управления в P.

Контроллер в виде модели динамической системы, блока системы управления или статической матрицы усиления. Контроллер может какой-либо иметь типы модели что P может быть, настолько же долго как P*C имеет то же количество вводов и выводов. loopsens вычисляет функции чувствительности, принимающие отрицательную обратную связь система с обратной связью. Чтобы вычислить функции чувствительности для системы с положительной обратной связью, используйте loopsens(P,-C).

loopsens команда принимает одну архитектуру управления степени свободы. Если у вас есть две архитектуры степени свободы, то создайте C включать только компенсатор в путь к обратной связи, не любые ссылочные каналы.

Выходные аргументы

свернуть все

Функции чувствительности обратной связи feedback(P,C), возвращенный в структуре, показывающей поля в приведенной ниже таблице. Функции чувствительности возвращены как пространство состояний (ss) модели тех же размерностей ввода-вывода как C*P. Если P или C модель данных частотной характеристики, затем функциями чувствительности является frd модели.

Поле

Описание

Si

Функция чувствительности входа к объекту.

Ti

Вход к объекту дополнительная функция чувствительности.

Li

Передаточная функция цикла входа к объекту.

So

Функция чувствительности выхода к объекту.

To

Выход к объекту дополнительная функция чувствительности.

Lo

Передаточная функция цикла выхода к объекту.

PSi

Функция чувствительности входа к объекту времен объекта.

CSo

Времена компенсатора функция чувствительности выхода к объекту.

Poles

Полюса замкнутого цикла feedback(P,C). Если любой P или C модель данных частотной характеристики, затем этим полем является NaN.

Stable

1, если номинальный замкнутый цикл устойчив, 0 в противном случае. Если любой P или C модель данных частотной характеристики, затем этим полем является NaN.

Больше о

свернуть все

Функции чувствительности

Структура межсоединений с обратной связью, показанная ниже, задает чувствительность ввода/вывода, дополнительную чувствительность и передаточные функции цикла. Структура включает многомерные системы в который P и C системы MIMO.

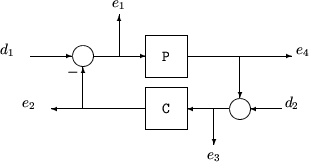
Control structure feedback(P,C) for computing sensitivity functions. The structure includes disturbance inputs d1 (plant input) and d2 (controller input), and measurement outputs e1 (plant input), e2 (controller output), e3 (controller input), and e4 (plant output).

Следующая таблица дает значения функций чувствительности ввода и вывода для этой структуры управления.

Описание

Уравнение

Введите чувствительность Si (передаточная функция с обратной связью от d 1 к e 1)

Si = (I + CP)–1

Введите дополнительную чувствительность Ti (передаточная функция с обратной связью от d 1 к e 2)

Ti = CP (I + CP)–1

Выведите чувствительность So (передаточная функция с обратной связью от d 2 к e 2)

So = (I + PC)–1

Выведите дополнительную чувствительность To (передаточная функция с обратной связью от d 2 к e 4)

To = PC (I + PC)–1

Введите передаточную функцию цикла Li

Li = CP

Выведите передаточную функцию цикла Lo

Lo = PC

Смотрите также

| | |

Представлено до R2006a

Документация Robust Control Toolbox

Поддержка