Exponenta Banner

undershoot

Метрики undershoot для переходов двухуровневых сигналов

свернуть все на странице

Синтаксис

us = undershoot(x)
us = undershoot(x,fs)
us = undershoot(x,t)
[us,uslev,usinst] = undershoot(___)
[___] = undershoot(___,Name,Value)
undershoot(___)

Описание

пример

us = undershoot(x) возвращает отклонение от номинала, описанное как процент различия между государственными уровнями во входном двухуровневом сигнале. Значения в us соответствуйте самым большим отклонениям ниже уровней конечного состояния каждого перехода.

us = undershoot(x,fs) задает частоту дискретизации fs в герц.

пример

us = undershoot(x,t) задает демонстрационные моменты t.

пример

[us,uslev,usinst] = undershoot(___) возвращает уровни uslev и демонстрационные моменты usinst из отклонений от номинала для каждого перехода. Задайте входную комбинацию от любого из предыдущих синтаксисов.

пример

[___] = undershoot(___,Name,Value) задает дополнительные опции с помощью одних или нескольких аргументов name-value.

пример

undershoot(___) строит двухуровневый сигнал и отмечает местоположение отклонения от номинала каждого перехода. Функция также строит более низкие и верхние моменты контрольного уровня и сопоставленные контрольные уровни и государственные уровни и сопоставленный ниже - и верхние государственные границы.

Примеры

свернуть все

Скрипт Open Live Script

Определите максимальное отклонение от номинала процента относительно высокого государственного уровня в 2,3-вольтовой форме волны часов.

Загрузите 2,3-вольтовые данные о часах. Определите максимальное отклонение от номинала процента перехода. Определите также уровень и демонстрационный момент отклонения от номинала. В этом примере максимальное отклонение от номинала в области постперехода происходит около индекса 23.

load('transitionex.mat','x')

[uu,lv,nst] = undershoot(x)
uu = 4.5012

lv = 2.1826

nst = 23

Постройте форму волны. Аннотируйте перерегулирование и соответствующий демонстрационный момент.

undershoot(x);

ax = gca;
ax.XTick = sort([ax.XTick nst]);

Figure Undershoot Plot contains an axes object. The axes object contains 12 objects of type line. These objects represent signal, upper cross, lower cross, post-undershoot, upper boundary, upper state, lower boundary, upper reference, lower reference, lower state.

Скрипт Open Live Script

Определите максимальное отклонение от номинала процента относительно высокого государственного уровня, уровня отклонения от номинала, и демонстрационный момент в 2,3-вольтовой форме волны часов.

Загрузите 2,3-вольтовые данные о часах с выборкой моментов. Данные о часах производятся на уровне 4 МГц.

load('transitionex.mat','x','t')

Определите максимальное отклонение от номинала процента, уровень отклонения от номинала в вольтах, и момент времени, где максимальное отклонение от номинала происходит. Постройте результат.

[us,uslev,usinst] = undershoot(x,t)
us = 4.5012

uslev = 2.1826

usinst = 5.5000e-06

undershoot(x,t);

Figure Undershoot Plot contains an axes object. The axes object contains 12 objects of type line. These objects represent signal, upper cross, lower cross, post-undershoot, upper boundary, upper state, lower boundary, upper reference, lower reference, lower state.

Скрипт Open Live Script

Определите максимальное отклонение от номинала процента относительно низкого государственного уровня, уровня отклонения от номинала, и демонстрационный момент в 2,3-вольтовой форме волны часов. Задайте 'Region' как 'Preshoot' выводить метрики перед переходом.

Загрузите 2,3-вольтовые данные о часах с выборкой моментов. Данные о часах производятся на уровне 4 МГц.

load('transitionex.mat','x','t')

Определите максимальное отклонение от номинала процента, уровень отклонения от номинала в вольтах, и момент выборки, где максимальное отклонение от номинала происходит. Постройте результат.

[us,uslev,usinst] = undershoot(x,t,'Region','Preshoot')
us = 6.1798

uslev = -0.1500

usinst = 5.0000e-06

undershoot(x,t,'Region','Preshoot');

Figure Undershoot Plot contains an axes object. The axes object contains 12 objects of type line. These objects represent signal, upper cross, lower cross, pre-undershoot, upper boundary, upper state, lower boundary, upper reference, lower reference, lower state.

Входные параметры

свернуть все

Двухуровневый сигнал в виде строки с действительным знаком или вектор-столбца. Демонстрационные моменты в X соответствуйте векторным индексам. Первый демонстрационный момент в x соответствует t = 0.

Частота дискретизации в герц в виде действительной положительной скалярной величины. Частота дискретизации определяет демонстрационные моменты, соответствуя элементам в x.

Демонстрационные моменты в виде вектора. Длина t должен равняться длине входного двухуровневого сигнала x.

Аргументы name-value

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'Tolerance',5 вычисляет отклонение от номинала с 5%-й областью допуска.

Контрольные уровни как процент амплитуды формы волны в виде 1 2 вектора с действительным знаком. Функция задает более низкий государственный уровень, чтобы быть 0 процентов и верхний государственный уровень, чтобы быть 100 процентов. Первый элемент соответствует более низкому контрольному уровню процента, и второй элемент соответствует верхнему контрольному уровню процента.

Область аберрации, по которой можно вычислить отклонение от номинала в виде 'Preshoot' или 'Postshoot'. Если вы задаете 'Preshoot', функция задает конец области аберрации перед переходом как прошлый момент, когда сигнал выходит из первого состояния. Если вы задаете 'Postshoot', функция задает запуск области аберрации постперехода как момент, когда сигнал вводит второе состояние. По умолчанию функция вычисляет отклонения от номинала для областей аберрации постперехода.

Длительность области аберрации в виде скаляра с действительным знаком. Функция вычисляет отклонение от номинала по заданной длительности для каждого перехода как кратное соответствующей длительности перехода. Если ребро формы волны достигнуто, или полный прошедший переход обнаруживается, прежде чем длительность области аберрации протекает, длительность является усеченной к ребру формы волны или запуску прошедшего перехода.

Низко - и высокие государственные уровни в виде 1 2 вектора с действительным знаком. Первый элемент соответствует низкому государственному уровню, и второй элемент соответствует высокому государственному уровню входной формы волны.

Уровень терпимости в виде скаляра с действительным знаком. Функция описывает допуск как процент различия между верхним - и более низкими государственными уровнями. Начальные и итоговые уровни каждого перехода должны быть в соответствующих государственных уровнях.

Выходные аргументы

свернуть все

Отклонения от номинала, описанные как процент государственных уровней, возвращенных как вектор. Длина us соответствует количеству переходов, обнаруженных во входном сигнале. Для получения дополнительной информации смотрите Отклонение от номинала.

Уровень отклонения от номинала, возвращенный как вектор-столбец.

Демонстрационные моменты отклонений от номинала предварительного перехода или постперехода, возвращенных как вектор-столбец. Если вы задаете fs или t, моменты отклонения от номинала находятся в секундах. Если вы не делаете specifyfs или t, моменты отклонения от номинала являются индексами входного вектора.

Больше о

свернуть все

Оценка уровней состояний

Определить переходы, undershoot функционируйте оценивает государственные уровни входного двухуровневого сигнала x методом гистограммы с этими шагами.

  1. Определите минимальные и максимальные амплитуды данных.

  2. Для конкретного количества интервалов гистограммы определите ширину интервала, которая является отношением амплитудной области значений к количеству интервалов.

  3. Сортировка значений данных в интервалы гистограммы.

  4. Идентифицируйте самые низкие и самые высокие индексируемые интервалы гистограммы с ненулевыми количествами.

  5. Разделите гистограмму на две подгистограммы.

  6. Вычислите государственные уровни путем определения режима или среднего значения верхних и более низких гистограмм.

Функция идентифицирует все области, которые пересекают верхнюю государственную границу низкого состояния и более низкую государственную границу высокого состояния. Низкое состояние и высокие государственные границы описываются как государственный уровень плюс или минус кратное различию между государственными уровнями.

Отклонение от номинала

Функция вычисляет проценты отклонения от номинала на основе самого большого отклонения от уровня конечного состояния в каждом переходе.

Для положительного движения (положительная полярность) импульс отклонением от номинала дают

100(S2−U)(S2−S1)

где U является самым большим отклонением ниже высокого государственного уровня, S 2 является высоким состоянием, и S 1 является низким состоянием.

Для отрицательного движения (отрицательная полярность) импульс отклонением от номинала дают

100(S1−U)(S2−S1)

Этот рисунок показывает вычисление отклонения от номинала для положительно идущего перехода.

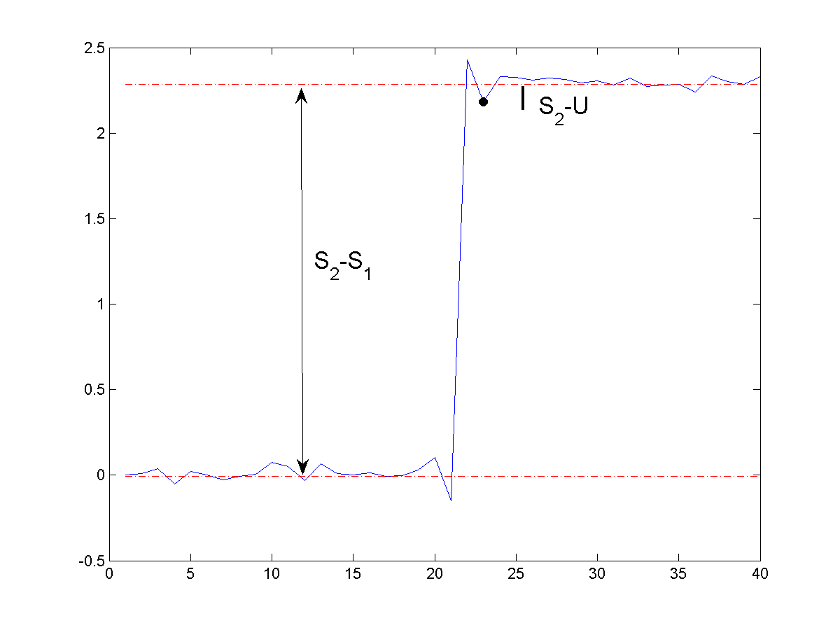
Красные пунктирные линии указывают на предполагаемые государственные уровни. Двусторонняя черная стрела изображает различие между верхним уровнем - и низкими государственными уровнями. Чистая черная линия указывает на различие между высоким государственным уровнем и значением отклонения от номинала.

Допуски государственного уровня

Каждый государственный уровень мог сопоставить ниже - и верхние государственные границы. Эти государственные границы заданы как государственный уровень плюс или минус скалярное кратное различие между высоким состоянием и низким состоянием. Чтобы обеспечить полезную область допуска, скаляр обычно является небольшим числом, таким как 2/100 или 3/100. В общем случае$\alpha\%$ область для низкого состояния задана как

$$S_1\pm{\alpha\over{100}}(S_2-S_1),$$

где$S_1$ низкий государственный уровень и$S_2$ является высоким государственным уровнем. Замените первый термин в уравнении с$S_2$ получить$\alpha\%$ область допуска для высокого состояния.

Этот рисунок иллюстрирует более низкие и верхние 5% государственных границ (области допуска) для двухуровневого сигнала положительной полярности. Толстые пунктирные линии указывают на предполагаемые государственные уровни.

Ссылки

[1] Стандарт IEEE 181. IEEE® Стандарт на переходах, импульсах и связанных формах волны (2003): 15–17.

Смотрите также

| |

Представленный в R2012a

Документация Signal Processing Toolbox

Поддержка