Подбирайте модель Gaussian process regression (GPR)
gprMdl = fitrgp(Tbl,ResponseVarName)Tbl, где ResponseVarName имя переменной отклика в Tbl.
gprMdl = fitrgp(___,Name,Value)Name,Value парные аргументы.
Например, можно задать подходящий метод, метод предсказания, функцию ковариации или активный метод выбора набора. Можно также обучить перекрестную подтвержденную модель.
gprMdl RegressionGP объект. Для методов и свойств этого класса, смотрите RegressionGP страница класса.
Если вы обучаете перекрестную подтвержденную модель, то gprMdl RegressionPartitionedModel объект. Для последующего анализа на перекрестном подтвержденном объекте используйте методы RegressionPartitionedModel класс. Для методов этого класса смотрите RegressionPartitionedModel страница класса.
Этот пример использует данные о морском ушке [1], [2], от Репозитория Машинного обучения UCI [3]. Загрузите данные и сохраните их в вашей текущей папке с именем abalone.data.
Храните данные в таблицу. Отобразите первые семь строк.
tbl = readtable('abalone.data','Filetype','text',... 'ReadVariableNames',false); tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height',... 'WWeight','SWeight','VWeight','ShWeight','NoShellRings'}; tbl(1:7,:)
ans =
Sex Length Diameter Height WWeight SWeight VWeight ShWeight NoShellRings
___ ______ ________ ______ _______ _______ _______ ________ ____________
'M' 0.455 0.365 0.095 0.514 0.2245 0.101 0.15 15
'M' 0.35 0.265 0.09 0.2255 0.0995 0.0485 0.07 7
'F' 0.53 0.42 0.135 0.677 0.2565 0.1415 0.21 9
'M' 0.44 0.365 0.125 0.516 0.2155 0.114 0.155 10
'I' 0.33 0.255 0.08 0.205 0.0895 0.0395 0.055 7
'I' 0.425 0.3 0.095 0.3515 0.141 0.0775 0.12 8
'F' 0.53 0.415 0.15 0.7775 0.237 0.1415 0.33 20Набор данных имеет 4 177 наблюдений. Цель состоит в том, чтобы предсказать возраст морского ушка от восьми физических измерений. Последняя переменная, количество звонков интерпретатора показывает возраст морского ушка. Первый предиктор является категориальной переменной. Последняя переменная в таблице является переменной отклика.
Подбирайте модель GPR с помощью подмножества метода регрессоров для оценки параметра и полностью независимого условного метода для предсказания. Стандартизируйте предикторы.
gprMdl = fitrgp(tbl,'NoShellRings','KernelFunction','ardsquaredexponential',... 'FitMethod','sr','PredictMethod','fic','Standardize',1)
grMdl =
RegressionGP
PredictorNames: {1x8 cell}
ResponseName: 'Var9'
ResponseTransform: 'none'
NumObservations: 4177
KernelFunction: 'ARDSquaredExponential'
KernelInformation: [1x1 struct]
BasisFunction: 'Constant'
Beta: 10.9148
Sigma: 2.0243
PredictorLocation: [10x1 double]
PredictorScale: [10x1 double]
Alpha: [1000x1 double]
ActiveSetVectors: [1000x10 double]
PredictMethod: 'FIC'
ActiveSetSize: 1000
FitMethod: 'SR'
ActiveSetMethod: 'Random'
IsActiveSetVector: [4177x1 logical]
LogLikelihood: -9.0013e+03
ActiveSetHistory: [1x1 struct]
BCDInformation: []
Предскажите ответы с помощью обученной модели.
ypred = resubPredict(gprMdl);
Постройте истинный ответ и предсказанные ответы.
figure(); plot(tbl.NoShellRings,'r.'); hold on plot(ypred,'b'); xlabel('x'); ylabel('y'); legend({'data','predictions'},'Location','Best'); axis([0 4300 0 30]); hold off;
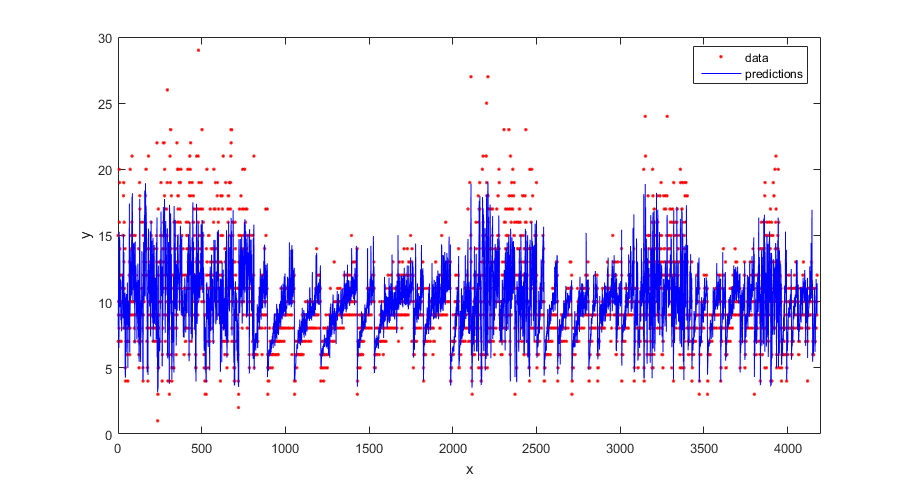
Вычислите потерю регрессии на обучающих данных (потеря перезамены) для обученной модели.
L = resubLoss(gprMdl)
L =
4.0064Сгенерируйте выборочные данные.
rng(0,'twister'); % For reproducibility n = 1000; x = linspace(-10,10,n)'; y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);
Подбирайте модель GPR с помощью линейной основной функции и точного подходящего метода, чтобы оценить параметры. Также используйте точный метод предсказания.
gprMdl = fitrgp(x,y,'Basis','linear',... 'FitMethod','exact','PredictMethod','exact');
Предскажите ответ, соответствующий строкам x (предсказания перезамены) использование обученной модели.
ypred = resubPredict(gprMdl);
Постройте истинный ответ с ожидаемыми значениями.
plot(x,y,'b.'); hold on; plot(x,ypred,'r','LineWidth',1.5); xlabel('x'); ylabel('y'); legend('Data','GPR predictions'); hold off

Загрузите выборочные данные.
load('gprdata2.mat')Данные имеют один переменный предиктор и непрерывный ответ. Это - симулированные данные.
Подбирайте модель GPR с помощью экспоненциальной функции ядра в квадрате параметрами ядра по умолчанию.
gprMdl1 = fitrgp(x,y,'KernelFunction','squaredexponential');
Теперь подбирайте вторую модель, где вы задаете начальные значения для параметров ядра.
sigma0 = 0.2; kparams0 = [3.5, 6.2]; gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential',... 'KernelParameters',kparams0,'Sigma',sigma0);
Вычислите предсказания перезамены из обеих моделей.
ypred1 = resubPredict(gprMdl1); ypred2 = resubPredict(gprMdl2);
Постройте предсказания ответа из обеих моделей и ответов в обучающих данных.
figure(); plot(x,y,'r.'); hold on plot(x,ypred1,'b'); plot(x,ypred2,'g'); xlabel('x'); ylabel('y'); legend({'data','default kernel parameters',... 'kparams0 = [3.5,6.2], sigma0 = 0.2'},... 'Location','Best'); title('Impact of initial kernel parameter values'); hold off
![Figure contains an axes object. The axes object with title Impact of initial kernel parameter values contains 3 objects of type line. These objects represent data, default kernel parameters, kparams0 = [3.5,6.2], sigma0 = 0.2.](../examples/stats/win64/ImpactofSpecifyingInitialKernelParameterValuesExample_01.png)
Крайняя логарифмическая вероятность, что fitrgp максимизирует, чтобы оценить, что параметры GPR имеют несколько локальных решений; решение, к которому это сходится, зависит от начальной точки. Каждое локальное решение соответствует конкретной интерпретации данных. В этом примере решение начальными параметрами ядра по умолчанию соответствует низкочастотному сигналу с высоким шумом, тогда как второе решение пользовательскими начальными параметрами ядра соответствует высокочастотному сигналу с низким шумом.
Загрузите выборочные данные.
load('gprdata.mat')Существует шесть непрерывных переменных предикторов. Существует 500 наблюдений в обучающем наборе данных и 100 наблюдений в наборе тестовых данных. Это - симулированные данные.
Подбирайте модель GPR с помощью экспоненциальной функции ядра в квадрате с отдельной шкалой расстояний для каждого предиктора. Эта функция ковариации задана как:
где представляет шкалу расстояний для предиктора , = 1, 2, ..., и стандартное отклонение сигнала. Неограниченная параметризация
Инициализируйте шкалы расстояний функции ядра в 10 и и шумовых стандартных отклонений сигнала в стандартном отклонении ответа.
sigma0 = std(ytrain); sigmaF0 = sigma0; d = size(Xtrain,2); sigmaM0 = 10*ones(d,1);
Подбирайте модель GPR с помощью начальных значений параметров ядра. Стандартизируйте предикторы в обучающих данных. Используйте точный подбор кривой и методы предсказания.
gprMdl = fitrgp(Xtrain,ytrain,'Basis','constant','FitMethod','exact',... 'PredictMethod','exact','KernelFunction','ardsquaredexponential',... 'KernelParameters',[sigmaM0;sigmaF0],'Sigma',sigma0,'Standardize',1);
Вычислите потерю регрессии на тестовых данных.
L = loss(gprMdl,Xtest,ytest)
L = 0.6919
Доступ к информации о ядре.
gprMdl.KernelInformation
ans = struct with fields:
Name: 'ARDSquaredExponential'
KernelParameters: [7x1 double]
KernelParameterNames: {7x1 cell}
Отобразите названия параметра ядра.
gprMdl.KernelInformation.KernelParameterNames
ans = 7x1 cell
{'LengthScale1'}
{'LengthScale2'}
{'LengthScale3'}
{'LengthScale4'}
{'LengthScale5'}
{'LengthScale6'}
{'SigmaF' }
Отобразите параметры ядра.
sigmaM = gprMdl.KernelInformation.KernelParameters(1:end-1,1)
sigmaM = 6×1
104 ×
0.0004
0.0007
0.0004
5.2711
0.1018
0.0056
sigmaF = gprMdl.KernelInformation.KernelParameters(end)
sigmaF = 28.1721
sigma = gprMdl.Sigma
sigma = 0.8162
Постройте журнал изученных шкал расстояний.
figure() plot((1:d)',log(sigmaM),'ro-'); xlabel('Length scale number'); ylabel('Log of length scale');

Журнал шкалы расстояний для 4-х и 5-х переменных предикторов высок относительно других. Эти переменные предикторы, кажется, как не влияют на ответ как другие переменные предикторы.
Подбирайте модель GPR, не используя 4-е и 5-е переменные в качестве переменных предикторов.
X = [Xtrain(:,1:3) Xtrain(:,6)]; sigma0 = std(ytrain); sigmaF0 = sigma0; d = size(X,2); sigmaM0 = 10*ones(d,1); gprMdl = fitrgp(X,ytrain,'Basis','constant','FitMethod','exact',... 'PredictMethod','exact','KernelFunction','ardsquaredexponential',... 'KernelParameters',[sigmaM0;sigmaF0],'Sigma',sigma0,'Standardize',1);
Вычислите ошибку регрессии на тестовых данных.
xtest = [Xtest(:,1:3) Xtest(:,6)]; L = loss(gprMdl,xtest,ytest)
L = 0.6928
Потеря похожа на ту, когда все переменные используются в качестве переменных предикторов.
Вычислите предсказанный ответ для тестовых данных.
ypred = predict(gprMdl,xtest);
Постройте исходный ответ наряду с подходящими значениями.
figure; plot(ytest,'r'); hold on; plot(ypred,'b'); legend('True response','GPR predicted values','Location','Best'); hold off

В этом примере показано, как оптимизировать гиперпараметры автоматически с помощью fitrgp. Пример использует gprdata2 данные, которые поставляются с вашим программным обеспечением.
Загрузите данные.
load('gprdata2.mat')Данные имеют один переменный предиктор и непрерывный ответ. Это - симулированные данные.
Подбирайте модель GPR с помощью экспоненциальной функции ядра в квадрате параметрами ядра по умолчанию.
gprMdl1 = fitrgp(x,y,'KernelFunction','squaredexponential');
Найдите гиперпараметры, которые минимизируют пятикратную потерю перекрестной проверки при помощи автоматической гипероптимизации параметров управления.
Для воспроизводимости установите случайный seed и используйте 'expected-improvement-plus' функция захвата.
rng default gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential',... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',... struct('AcquisitionFunctionName','expected-improvement-plus'));
|======================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Sigma | | | result | log(1+loss) | runtime | (observed) | (estim.) | | |======================================================================================| | 1 | Best | 0.29417 | 3.0858 | 0.29417 | 0.29417 | 0.0015045 | | 2 | Best | 0.037898 | 2.0644 | 0.037898 | 0.060792 | 0.14147 | | 3 | Accept | 1.5693 | 1.2168 | 0.037898 | 0.040633 | 25.279 | | 4 | Accept | 0.29417 | 2.479 | 0.037898 | 0.037984 | 0.0001091 | | 5 | Accept | 0.29393 | 2.4371 | 0.037898 | 0.038029 | 0.029932 | | 6 | Accept | 0.13152 | 1.4567 | 0.037898 | 0.038127 | 0.37127 | | 7 | Best | 0.037785 | 2.4513 | 0.037785 | 0.037728 | 0.18116 | | 8 | Accept | 0.03783 | 2.6087 | 0.037785 | 0.036524 | 0.16251 | | 9 | Accept | 0.037833 | 2.8548 | 0.037785 | 0.036854 | 0.16159 | | 10 | Accept | 0.037835 | 2.8792 | 0.037785 | 0.037052 | 0.16072 | | 11 | Accept | 0.29417 | 2.8583 | 0.037785 | 0.03705 | 0.00038214 | | 12 | Accept | 0.42256 | 1.6664 | 0.037785 | 0.03696 | 3.2067 | | 13 | Accept | 0.03786 | 3.3164 | 0.037785 | 0.037087 | 0.15245 | | 14 | Accept | 0.29417 | 2.9484 | 0.037785 | 0.037043 | 0.0063584 | | 15 | Accept | 0.42302 | 1.9308 | 0.037785 | 0.03725 | 1.2221 | | 16 | Accept | 0.039486 | 2.1424 | 0.037785 | 0.037672 | 0.10069 | | 17 | Accept | 0.038591 | 1.3666 | 0.037785 | 0.037687 | 0.12077 | | 18 | Accept | 0.038513 | 1.6086 | 0.037785 | 0.037696 | 0.1227 | | 19 | Best | 0.037757 | 2.8048 | 0.037757 | 0.037572 | 0.19621 | | 20 | Accept | 0.037787 | 2.7099 | 0.037757 | 0.037601 | 0.18068 | |======================================================================================| | Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Sigma | | | result | log(1+loss) | runtime | (observed) | (estim.) | | |======================================================================================| | 21 | Accept | 0.44917 | 1.7788 | 0.037757 | 0.03766 | 8.7818 | | 22 | Accept | 0.040201 | 2.3177 | 0.037757 | 0.037601 | 0.075414 | | 23 | Accept | 0.040142 | 2.158 | 0.037757 | 0.037607 | 0.087198 | | 24 | Accept | 0.29417 | 2.8936 | 0.037757 | 0.03758 | 0.0031018 | | 25 | Accept | 0.29417 | 2.6058 | 0.037757 | 0.037555 | 0.00019545 | | 26 | Accept | 0.29417 | 2.8697 | 0.037757 | 0.037582 | 0.013608 | | 27 | Accept | 0.29417 | 2.8458 | 0.037757 | 0.037556 | 0.00076147 | | 28 | Accept | 0.42162 | 1.8276 | 0.037757 | 0.037854 | 0.6791 | | 29 | Best | 0.037704 | 2.3186 | 0.037704 | 0.037908 | 0.2367 | | 30 | Accept | 0.037725 | 3.4969 | 0.037704 | 0.037881 | 0.21743 |


__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 97.0699 seconds
Total objective function evaluation time: 71.9991
Best observed feasible point:
Sigma
______
0.2367
Observed objective function value = 0.037704
Estimated objective function value = 0.038223
Function evaluation time = 2.3186
Best estimated feasible point (according to models):
Sigma
_______
0.16159
Estimated objective function value = 0.037881
Estimated function evaluation time = 2.2999
Сравните пред - и подгонки постоптимизации.
ypred1 = resubPredict(gprMdl1); ypred2 = resubPredict(gprMdl2); figure(); plot(x,y,'r.'); hold on plot(x,ypred1,'b'); plot(x,ypred2,'k','LineWidth',2); xlabel('x'); ylabel('y'); legend({'data','Initial Fit','Optimized Fit'},'Location','Best'); title('Impact of Optimization'); hold off

Этот пример использует данные о морском ушке [1], [2], от Репозитория Машинного обучения UCI [3]. Загрузите данные и сохраните их в вашей текущей папке с именем abalone.data.
Храните данные в table. Отобразите первые семь строк.
tbl = readtable('abalone.data','Filetype','text','ReadVariableNames',false); tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height','WWeight','SWeight','VWeight','ShWeight','NoShellRings'}; tbl(1:7,:)
ans =
Sex Length Diameter Height WWeight SWeight VWeight ShWeight NoShellRings
___ ______ ________ ______ _______ _______ _______ ________ ____________
'M' 0.455 0.365 0.095 0.514 0.2245 0.101 0.15 15
'M' 0.35 0.265 0.09 0.2255 0.0995 0.0485 0.07 7
'F' 0.53 0.42 0.135 0.677 0.2565 0.1415 0.21 9
'M' 0.44 0.365 0.125 0.516 0.2155 0.114 0.155 10
'I' 0.33 0.255 0.08 0.205 0.0895 0.0395 0.055 7
'I' 0.425 0.3 0.095 0.3515 0.141 0.0775 0.12 8
'F' 0.53 0.415 0.15 0.7775 0.237 0.1415 0.33 20Набор данных имеет 4 177 наблюдений. Цель состоит в том, чтобы предсказать возраст морского ушка от восьми физических измерений. Последняя переменная, количество звонков интерпретатора показывает возраст морского ушка. Первый предиктор является категориальной переменной. Последняя переменная в таблице является переменной отклика.
Обучите перекрестную подтвержденную модель GPR с помощью 25% данных для валидации.
rng('default') % For reproducibility cvgprMdl = fitrgp(tbl,'NoShellRings','Standardize',1,'Holdout',0.25);
Вычислите среднюю потерю на моделях использования сгибов, обученных на наблюдениях из сгиба.
kfoldLoss(cvgprMdl)
ans = 4.6409
Предскажите ответы для данных из сгиба.
ypred = kfoldPredict(cvgprMdl);
Постройте истинные ответы, используемые для тестирования и предсказаний.
figure(); plot(ypred(cvgprMdl.Partition.test)); hold on; y = table2array(tbl(:,end)); plot(y(cvgprMdl.Partition.test),'r.'); axis([0 1050 0 30]); xlabel('x') ylabel('y') hold off;
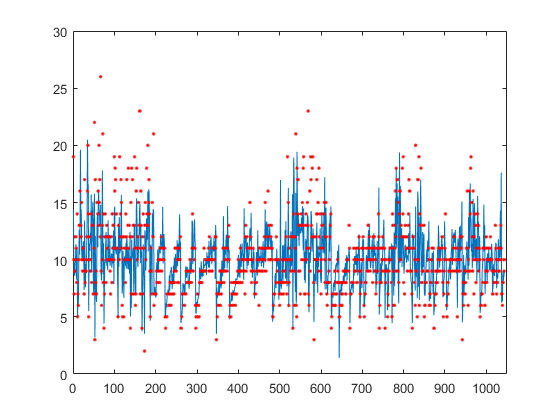
Сгенерируйте выборочные данные.
rng(0,'twister'); % For reproducibility n = 1000; x = linspace(-10,10,n)'; y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);
Задайте экспоненциальную функцию ядра в квадрате как пользовательскую функцию ядра.
Можно вычислить экспоненциальную функцию ядра в квадрате как
где стандартное отклонение сигнала, шкала расстояний. Оба и должен быть больше нуля. Это условие может быть осуществлено неограниченной параметризацией, и , для некоторого неограниченного вектора параметризации .
Следовательно, можно задать экспоненциальную функцию ядра в квадрате как пользовательскую функцию ядра можно следующим образом:
kfcn = @(XN,XM,theta) (exp(theta(2))^2)*exp(-(pdist2(XN,XM).^2)/(2*exp(theta(1))^2));
Здесь pdist2(XN,XM).^2 вычисляет матрицу расстояния.
Подбирайте модель GPR с помощью пользовательской функции ядра, kfcn. Задайте начальные значения параметров ядра (Поскольку вы используете пользовательскую функцию ядра, необходимо ввести начальные значения для неограниченного вектора параметризации, theta).
theta0 = [1.5,0.2]; gprMdl = fitrgp(x,y,'KernelFunction',kfcn,'KernelParameters',theta0);
fitrgp использует аналитические производные, чтобы оценить параметры при использовании встроенной функции ядра, тогда как при использовании пользовательского ядра функционируют, это использует числовые производные.
Вычислите потерю перезамены для этой модели.
L = resubLoss(gprMdl)
L = 0.0391
Подбирайте модель GPR с помощью встроенной экспоненциальной опции функции ядра в квадрате. Задайте начальные значения параметров ядра (Поскольку вы используете встроенную пользовательскую функцию ядра и задающий начальные значения параметров, необходимо ввести начальные значения для стандартного отклонения сигнала и шкалы (шкал) расстояний непосредственно).
sigmaL0 = exp(1.5); sigmaF0 = exp(0.2); gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential','KernelParameters',[sigmaL0,sigmaF0]);
Вычислите потерю перезамены для этой модели.
L2 = resubLoss(gprMdl2)
L2 = 0.0391
Два значения потерь эквивалентны ожидаемый.
Обучите модель GPR на сгенерированных данных со многими предикторами. Задайте начальный размер шага для оптимизатора LBFGS.
Установите seed и тип генератора случайных чисел для воспроизводимости результатов.
rng(0,'twister'); % For reproducibility
Сгенерируйте выборочные данные с 300 наблюдениями и 3 000 предикторов, где переменная отклика зависит от 4-х, 7-х, и 13-х предикторов.
N = 300; P = 3000; X = rand(N,P); y = cos(X(:,7)) + sin(X(:,4).*X(:,13)) + 0.1*randn(N,1);
Установите начальные значения для параметров ядра.
sigmaL0 = sqrt(P)*ones(P,1); % Length scale for predictors sigmaF0 = 1; % Signal standard deviation
Установите начальное шумовое стандартное отклонение на 1.
sigmaN0 = 1;
Specify 1e-2 как допуск завершения к относительной норме градиента.
opts = statset('fitrgp');
opts.TolFun = 1e-2;Подбирайте модель GPR с помощью начальных значений параметров ядра, начального шумового стандартного отклонения, и автоматическое определение уместности (ARD) придало экспоненциальной функции ядра квадратную форму.
Задайте начальный размер шага как 1 для определения начального приближения Гессиана для оптимизатора LBFGS.
gpr = fitrgp(X,y,'KernelFunction','ardsquaredexponential','Verbose',1, ... 'Optimizer','lbfgs','OptimizerOptions',opts, ... 'KernelParameters',[sigmaL0;sigmaF0],'Sigma',sigmaN0,'InitialStepSize',1);
o Parameter estimation: FitMethod = Exact, Optimizer = lbfgs
o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 0 | 3.004966e+02 | 2.569e+02 | 0.000e+00 | | 3.893e-03 | 0.000e+00 | YES |
| 1 | 9.525779e+01 | 1.281e+02 | 1.003e+00 | OK | 6.913e-03 | 1.000e+00 | YES |
| 2 | 3.972026e+01 | 1.647e+01 | 7.639e-01 | OK | 4.718e-03 | 5.000e-01 | YES |
| 3 | 3.893873e+01 | 1.073e+01 | 1.057e-01 | OK | 3.243e-03 | 1.000e+00 | YES |
| 4 | 3.859904e+01 | 5.659e+00 | 3.282e-02 | OK | 3.346e-03 | 1.000e+00 | YES |
| 5 | 3.748912e+01 | 1.030e+01 | 1.395e-01 | OK | 1.460e-03 | 1.000e+00 | YES |
| 6 | 2.028104e+01 | 1.380e+02 | 2.010e+00 | OK | 2.326e-03 | 1.000e+00 | YES |
| 7 | 2.001849e+01 | 1.510e+01 | 9.685e-01 | OK | 2.344e-03 | 1.000e+00 | YES |
| 8 | -7.706109e+00 | 8.340e+01 | 1.125e+00 | OK | 5.771e-04 | 1.000e+00 | YES |
| 9 | -1.786074e+01 | 2.323e+02 | 2.647e+00 | OK | 4.217e-03 | 1.250e-01 | YES |
| 10 | -4.058422e+01 | 1.972e+02 | 6.796e-01 | OK | 7.035e-03 | 1.000e+00 | YES |
| 11 | -7.850209e+01 | 4.432e+01 | 8.335e-01 | OK | 3.099e-03 | 1.000e+00 | YES |
| 12 | -1.312162e+02 | 3.334e+01 | 1.277e+00 | OK | 5.432e-02 | 1.000e+00 | YES |
| 13 | -2.005064e+02 | 9.519e+01 | 2.828e+00 | OK | 5.292e-03 | 1.000e+00 | YES |
| 14 | -2.070150e+02 | 1.898e+01 | 1.641e+00 | OK | 6.817e-03 | 1.000e+00 | YES |
| 15 | -2.108086e+02 | 3.793e+01 | 7.685e-01 | OK | 3.479e-03 | 1.000e+00 | YES |
| 16 | -2.122920e+02 | 7.057e+00 | 1.591e-01 | OK | 2.055e-03 | 1.000e+00 | YES |
| 17 | -2.125610e+02 | 4.337e+00 | 4.818e-02 | OK | 1.974e-03 | 1.000e+00 | YES |
| 18 | -2.130162e+02 | 1.178e+01 | 8.891e-02 | OK | 2.856e-03 | 1.000e+00 | YES |
| 19 | -2.139378e+02 | 1.933e+01 | 2.371e-01 | OK | 1.029e-02 | 1.000e+00 | YES |
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 20 | -2.151111e+02 | 1.550e+01 | 3.015e-01 | OK | 2.765e-02 | 1.000e+00 | YES |
| 21 | -2.173046e+02 | 5.856e+00 | 6.537e-01 | OK | 1.414e-02 | 1.000e+00 | YES |
| 22 | -2.201781e+02 | 8.918e+00 | 8.484e-01 | OK | 6.381e-03 | 1.000e+00 | YES |
| 23 | -2.288858e+02 | 4.846e+01 | 2.311e+00 | OK | 2.661e-03 | 1.000e+00 | YES |
| 24 | -2.392171e+02 | 1.190e+02 | 6.283e+00 | OK | 8.113e-03 | 1.000e+00 | YES |
| 25 | -2.511145e+02 | 1.008e+02 | 1.198e+00 | OK | 1.605e-02 | 1.000e+00 | YES |
| 26 | -2.742547e+02 | 2.207e+01 | 1.231e+00 | OK | 3.191e-03 | 1.000e+00 | YES |
| 27 | -2.849931e+02 | 5.067e+01 | 3.660e+00 | OK | 5.184e-03 | 1.000e+00 | YES |
| 28 | -2.899797e+02 | 2.068e+01 | 1.162e+00 | OK | 6.270e-03 | 1.000e+00 | YES |
| 29 | -2.916723e+02 | 1.816e+01 | 3.213e-01 | OK | 1.415e-02 | 1.000e+00 | YES |
| 30 | -2.947674e+02 | 6.965e+00 | 1.126e+00 | OK | 6.339e-03 | 1.000e+00 | YES |
| 31 | -2.962491e+02 | 1.349e+01 | 2.352e-01 | OK | 8.999e-03 | 1.000e+00 | YES |
| 32 | -3.004921e+02 | 1.586e+01 | 9.880e-01 | OK | 3.940e-02 | 1.000e+00 | YES |
| 33 | -3.118906e+02 | 1.889e+01 | 3.318e+00 | OK | 1.213e-01 | 1.000e+00 | YES |
| 34 | -3.189215e+02 | 7.086e+01 | 3.070e+00 | OK | 8.095e-03 | 1.000e+00 | YES |
| 35 | -3.245557e+02 | 4.366e+00 | 1.397e+00 | OK | 2.718e-03 | 1.000e+00 | YES |
| 36 | -3.254613e+02 | 3.751e+00 | 6.546e-01 | OK | 1.004e-02 | 1.000e+00 | YES |
| 37 | -3.262823e+02 | 4.011e+00 | 2.026e-01 | OK | 2.441e-02 | 1.000e+00 | YES |
| 38 | -3.325606e+02 | 1.773e+01 | 2.427e+00 | OK | 5.234e-02 | 1.000e+00 | YES |
| 39 | -3.350374e+02 | 1.201e+01 | 1.603e+00 | OK | 2.674e-02 | 1.000e+00 | YES |
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 40 | -3.379112e+02 | 5.280e+00 | 1.393e+00 | OK | 1.177e-02 | 1.000e+00 | YES |
| 41 | -3.389136e+02 | 3.061e+00 | 7.121e-01 | OK | 2.935e-02 | 1.000e+00 | YES |
| 42 | -3.401070e+02 | 4.094e+00 | 6.224e-01 | OK | 3.399e-02 | 1.000e+00 | YES |
| 43 | -3.436291e+02 | 8.833e+00 | 1.707e+00 | OK | 5.231e-02 | 1.000e+00 | YES |
| 44 | -3.456295e+02 | 5.891e+00 | 1.424e+00 | OK | 3.772e-02 | 1.000e+00 | YES |
| 45 | -3.460069e+02 | 1.126e+01 | 2.580e+00 | OK | 3.907e-02 | 1.000e+00 | YES |
| 46 | -3.481756e+02 | 1.546e+00 | 8.142e-01 | OK | 1.565e-02 | 1.000e+00 | YES |
Infinity norm of the final gradient = 1.546e+00
Two norm of the final step = 8.142e-01, TolX = 1.000e-12
Relative infinity norm of the final gradient = 6.016e-03, TolFun = 1.000e-02
EXIT: Local minimum found.
o Alpha estimation: PredictMethod = Exact
Поскольку модель GPR использует ядро ARD со многими предикторами, использование приближения LBFGS к Гессиану использует память более эффективно, чем хранение полной матрицы Гессиана. Кроме того, использование начального размера шага, чтобы определить начальное приближение Гессиана может помочь ускорить оптимизацию.
Найдите веса предиктора путем взятия экспоненциала отрицательных изученных шкал расстояний. Нормируйте веса.
sigmaL = gpr.KernelInformation.KernelParameters(1:end-1); % Learned length scales weights = exp(-sigmaL); % Predictor weights weights = weights/sum(weights); % Normalized predictor weights
Постройте нормированные веса предиктора.
figure; semilogx(weights,'ro'); xlabel('Predictor index'); ylabel('Predictor weight');

Обученная модель GPR присваивает самые большие веса 4-м, 7-м, и 13-м предикторам. Несоответствующие предикторы имеют веса близко к нулю.
Tbl — Выборочные данныеtableВыборочные данные раньше обучали модель в виде table. Каждая строка Tbl соответствует одному наблюдению, и каждый столбец соответствует одной переменной. Tbl содержит переменные предикторы, и опционально это может также содержать один столбец для переменной отклика. Многостолбцовые переменные и массивы ячеек кроме массивов ячеек из символьных векторов не позволены.
Если Tbl содержит переменную отклика, и вы хотите использовать все остающиеся переменные в качестве предикторов, затем задать переменную отклика с помощью ResponseVarName.
Если Tbl содержит переменную отклика, и вы хотите использовать только подмножество предикторов в обучении модель, затем задать переменную отклика и переменные предикторы с помощью formula.
Если Tbl не содержит переменную отклика, затем задает переменную отклика с помощью y. Длина переменной отклика и количество строк в Tbl должно быть равным.
Для получения дополнительной информации о table тип данных, смотрите table.
Если ваши данные о предикторе содержат категориальные переменные, то fitrgp создает фиктивные переменные. Для получения дополнительной информации смотрите CategoricalPredictors.
Типы данных: table
ResponseVarName — Имя переменной откликаTblИмя переменной отклика в виде имени переменной в Tbl. Необходимо задать ResponseVarName как вектор символов или строковый скаляр. Например, если переменная отклика y хранится в Tbl (как Tbl.y), затем задайте его как 'y'. В противном случае программное обеспечение обрабатывает все столбцы Tbl, включая y, как предикторы, когда обучение модель.
Типы данных: char | string
formula — Переменные отклика и переменные предикторы, чтобы использовать в обучении модели'y~x1+x2+x3'Переменные отклика и переменные предикторы, чтобы использовать в обучении модели в виде вектора символов или строкового скаляра в форме 'y~x1+x2+x3'. В этой форме, y представляет переменную отклика; x1x2 , x3 представляйте переменные предикторы, чтобы использовать в обучении модель.
Используйте формулу, если вы хотите задать подмножество переменных в Tbl как предикторы, чтобы использовать, когда обучение модель. Если вы задаете формулу, то любые переменные, которые не появляются в formula не используются, чтобы обучить модель.
Имена переменных в формуле должны быть оба именами переменных в Tbl (Tbl.Properties.VariableNames) и допустимый MATLAB® идентификаторы. Можно проверить имена переменных в Tbl при помощи isvarname функция. Если имена переменных не допустимы, то можно преобразовать их при помощи matlab.lang.makeValidName функция.
Формула не указывает на форму BasisFunction.
Пример: 'PetalLength~PetalWidth+Species' идентифицирует переменную PetalLength как переменная отклика и PetalWidth и Species как переменные предикторы.
Типы данных: char | string
X — Данные о предикторе для модели GPRДанные о предикторе для модели GPR в виде n-by-d матрица. n является количеством наблюдений (строки), и d является количеством предикторов (столбцы).
Длина y и количество строк X должно быть равным.
Задавать имена предикторов в порядке их внешнего вида в X, используйте PredictorNames аргумент пары "имя-значение".
Типы данных: double
y — Данные об ответе для модели GPRДанные об ответе для модели GPR в виде n-by-1 вектор. Можно не использовать y если вы обеспечиваете Tbl обучающие данные, который также включает y. В этом случае используйте ResponseVarName идентифицировать переменную отклика или использовать formula идентифицировать переменные отклика и переменные предикторы.
Типы данных: double
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'FitMethod','sr','BasisFunction','linear','ActiveSetMethod','sgma','PredictMethod','fic' обучает модель GPR с помощью подмножества метода приближения регрессоров для оценки параметра, использует линейную основную функцию, использует разреженное жадное матричное приближение для активного выбора и полностью независимый условный метод приближения для предсказания.Примечание
Вы не можете использовать аргумент значения имени перекрестной проверки вместе с 'OptimizeHyperparameters' аргумент значения имени. Можно изменить перекрестную проверку для 'OptimizeHyperparameters' только при помощи 'HyperparameterOptimizationOptions' аргумент значения имени.
FitMethod — Метод, чтобы оценить параметры модели GPR'none' | 'exact' | 'sd' | 'sr' | 'fic'Метод, чтобы оценить параметры модели GPR в виде одного из следующих.
| Подходящий метод | Описание |
|---|---|
'none' | Никакая оценка, используйте начальные значения параметров в качестве известных значений параметров. |
'exact' | Точная Гауссова регрессия процесса. Значение по умолчанию, если n ≤ 2000, где n является количеством наблюдений. |
'sd' | Подмножество приближения точек данных. Значение по умолчанию, если n> 2000, где n является количеством наблюдений. |
'sr' | Подмножество приближения регрессоров. |
'fic' | Полностью независимое условное приближение. |
Пример: 'FitMethod','fic'
BasisFunction — Явный базис в модели GPR'constant' (значение по умолчанию) | 'none' | 'linear' | 'pureQuadratic' | указатель на функциюЯвный базис в модели GPR в виде одного из следующих. Если n является количеством наблюдений, основная функция добавляет термин H *β к модели, где H является базисной матрицей, и β является p-by-1 вектор из базисных коэффициентов.
| Явный базис | Базисная матрица |
|---|---|
'none' | Пустая матрица. |
'constant' |
(n-by-1 вектор 1 с, где n является количеством наблюдений), |
'linear' |
|
'pureQuadratic' |
где
|
| Указатель на функцию | Указатель на функцию, где |
Пример: 'BasisFunction','pureQuadratic'
Типы данных: char | string | function_handle
Beta — Начальное значение коэффициентовНачальное значение коэффициентов для явного базиса в виде p-by-1 вектор, где p является количеством столбцов в базисной матрице H.
Базисная матрица зависит от выбора явной основной функции можно следующим образом (также смотрите BasisFunction).
fitrgp использует содействующие начальные значения в качестве известных содействующих значений, только когда FitMethod 'none'.
Типы данных: double
Sigma — Начальное значение для шумового стандартного отклонения Гауссовой модели процессаstdY)/sqrt(2) (значение по умолчанию) | значение положительной скалярной величиныНачальное значение для шумового стандартного отклонения Гауссовой модели процесса в виде значения положительной скалярной величины.
fitrgp параметрирует шумовое стандартное отклонение как сумму SigmaLowerBound и exp(η), где η является неограниченным значением. Поэтому Sigma должно быть больше, чем SigmaLowerBound маленьким допуском так, чтобы функция могла инициализировать η к конечному значению. В противном случае функция сбрасывает Sigma к совместимому значению.
Допуском является 1e-3 когда ConstantSigma false (значение по умолчанию) и 1e-6 в противном случае. Если допуск не мал достаточно относительно шкалы переменной отклика, можно увеличить переменную отклика так, чтобы значение допуска могло быть рассмотрено маленьким для переменной отклика.
Пример: 'Sigma',2
Типы данных: double
ConstantSigma — Постоянное значение Sigma для шумового стандартного отклонения Гауссовой модели процессаfalse (значение по умолчанию) | trueПостоянное значение Sigma для шумового стандартного отклонения Гауссовой модели процесса в виде логического скаляра. Когда ConstantSigma true, fitrgp не оптимизирует значение Sigma, но вместо этого принимает начальное значение как значение в течение его расчетов.
Пример: 'ConstantSigma',true
Типы данных: логический
SigmaLowerBound — Нижняя граница на шумовом стандартном отклонении1e-2*stdY) (значение по умолчанию) | значение положительной скалярной величиныCategoricalPredictors — Категориальный список предикторов'all'Категориальные предикторы перечисляют в виде одного из значений в этой таблице.
| Значение | Описание |
|---|---|
| Вектор из положительных целых чисел |
Каждая запись в векторе является значением индекса, указывающим, что соответствующий предиктор является категориальным. Значения индекса между 1 и Если |
| Логический вектор |
|
| Символьная матрица | Каждая строка матрицы является именем переменного предиктора. Имена должны совпадать с записями в PredictorNames. Заполните имена дополнительными пробелами, таким образом, каждая строка символьной матрицы имеет ту же длину. |
| Массив строк или массив ячеек из символьных векторов | Каждым элементом в массиве является имя переменного предиктора. Имена должны совпадать с записями в PredictorNames. |
"all" | Все предикторы являются категориальными. |
По умолчанию, если данные о предикторе находятся в таблице (Tbl), fitrgp принимает, что переменная является категориальной, если это - логический вектор, категориальный вектор, символьный массив, массив строк или массив ячеек из символьных векторов. Если данные о предикторе являются матрицей (X), fitrgp принимает, что все предикторы непрерывны. Чтобы идентифицировать любые другие предикторы как категориальные предикторы, задайте их при помощи 'CategoricalPredictors' аргумент значения имени.
Для идентифицированных категориальных предикторов, fitrgp создает фиктивные переменные с помощью двух различных схем, в зависимости от того, не упорядочена ли категориальная переменная или упорядочена. Для неупорядоченной категориальной переменной, fitrgp создает одну фиктивную переменную для каждого уровня категориальной переменной. Для упорядоченной категориальной переменной, fitrgp создает тот меньше фиктивной переменной, чем количество категорий. Для получения дополнительной информации смотрите Автоматическое Создание Фиктивных Переменных.
Пример: 'CategoricalPredictors','all'
Типы данных: single | double | logical | char | string | cell
Standardize — Индикатор, чтобы стандартизировать данные0 (false) (значение по умолчанию) | логическое значениеИндикатор, чтобы стандартизировать данные в виде логического значения.
Если вы устанавливаете 'Standardize',1, затем центры программного обеспечения и шкалы каждый столбец данных о предикторе, столбцом среднее и стандартное отклонение, соответственно. Программное обеспечение не стандартизирует данные, содержавшиеся в фиктивных переменных столбцах, которые это генерирует для категориальных предикторов.
Пример: 'Standardize',1
Пример: 'Standardize',true
Типы данных: логический
Regularization — Стандартное отклонение регуляризации1e-2*stdY) (значение по умолчанию) | значение положительной скалярной величиныСтандартное отклонение регуляризации для разреженного подмножества методов регрессоров ('sr') и полностью независимое условное выражение ('fic') в виде значения положительной скалярной величины.
Пример: 'Regularization',0.2
Типы данных: double
ComputationMethod — Метод для вычисления логарифмической вероятности и градиента'qr' (значение по умолчанию) | 'v'Метод для вычисления логарифмической вероятности и градиента для оценки параметра с помощью подмножества регрессоров ('sr') и полностью независимое условное выражение ('fic') методы приближения в виде одного из следующих.
'qr' — Используйте основанный на QR-факторизации подход, эта опция обеспечивает лучшую точность.
'v' — Используйте подход V-method-based. Эта опция обеспечивает более быстрый расчет логарифмических градиентов вероятности.
Пример: 'ComputationMethod','v'
KernelFunction — Форма функции ковариации'squaredexponential' (значение по умолчанию) | 'exponential' | 'matern32' | 'matern52' | 'rationalquadratic' | 'ardsquaredexponential' | 'ardexponential' | 'ardmatern32' | 'ardmatern52' | 'ardrationalquadratic' | указатель на функциюФорма ковариации функционирует в виде одного из следующих.
| Функция | Описание |
|---|---|
'exponential' | Экспоненциальное ядро. |
'squaredexponential' | Экспоненциальное ядро в квадрате. |
'matern32' | Ядро Matern параметром 3/2. |
'matern52' | Ядро Matern параметром 5/2. |
'rationalquadratic' | Рациональное квадратичное ядро. |
'ardexponential' | Экспоненциальное ядро с отдельной шкалой расстояний на предиктор. |
'ardsquaredexponential' | Экспоненциальное ядро в квадрате с отдельной шкалой расстояний на предиктор. |
'ardmatern32' | Ядро Matern параметром 3/2 и отдельная шкала расстояний на предиктор. |
'ardmatern52' | Ядро Matern параметром 5/2 и отдельная шкала расстояний на предиктор. |
'ardrationalquadratic' | Рациональное квадратичное ядро с отдельной шкалой расстояний на предиктор. |
| Указатель на функцию | Указатель на функцию, который может быть назван как это:Kmn = kfcn(Xm,Xn,theta)
где Xm m-by-d матрица, Xn n-by-d матрица и Kmn m-by-n матрица продуктов ядра, таким образом что Kmn(i, j), продукт ядра между Xm(i, :) и XnJ. theta r-by-1 неограниченный вектор параметра для kfcn. |
Для получения дополнительной информации о функциях ядра смотрите Ядро (Ковариация) Опции Функции.
Пример: 'KernelFunction','matern32'
Типы данных: char | string | function_handle
KernelParameters — Начальные значения для параметров ядраНачальные значения для параметров ядра в виде вектора. Размер вектора и значений зависит от формы функции ковариации, заданной KernelFunction аргумент пары "имя-значение".
'KernelFunction' | 'KernelParameters' |
|---|---|
'exponential', 'squaredexponential', 'matern32', или 'matern52' | 2 1 векторный phi, где phi(1) содержит шкалу расстояний и phi(2) содержит стандартное отклонение сигнала. Начальное значение по умолчанию параметра шкалы расстояний является средним значением стандартных отклонений предикторов, и стандартное отклонение сигнала является стандартным отклонением ответов, разделенных на квадратный корень из 2. Таким образом, phi = [mean(std(X));std(y)/sqrt(2)] |
'rationalquadratic' | Векторный phi 3 на 1phi(1) содержит шкалу расстояний, phi(2) содержит параметр смеси шкалы и phi(3) содержит стандартное отклонение сигнала. Начальное значение по умолчанию параметра шкалы расстояний является средним значением стандартных отклонений предикторов, и стандартное отклонение сигнала является стандартным отклонением ответов, разделенных на квадратный корень из 2. Начальное значение по умолчанию для параметра смеси шкалы равняется 1. Таким образом, phi = [mean(std(X));1;std(y)/sqrt(2)] |
'ardexponential', 'ardsquaredexponential', 'ardmatern32', или 'ardmatern52' | (d +1)-by-1 векторный phi, где phi(i) содержит шкалу расстояний для предиктора i и phi(d+1) содержит стандартное отклонение сигнала. d является количеством переменных предикторов после того, как фиктивные переменные будут созданы для категориальных переменных. Для получения дополнительной информации о создании фиктивных переменных, смотрите CategoricalPredictors. Начальное значение по умолчанию параметров шкалы расстояний является стандартными отклонениями предикторов, и стандартное отклонение сигнала является стандартным отклонением ответов, разделенных на квадратный корень из 2. Таким образом, phi = [std(X)';std(y)/sqrt(2)] |
'ardrationalquadratic' | (d +2)-by-1 векторный phi, где phi(i) содержит шкалу расстояний для предиктора i, phi(d+1) содержит параметр смеси шкалы и phi(d+2) содержит стандартное отклонение сигнала.Начальное значение по умолчанию параметров шкалы расстояний является стандартными отклонениями предикторов, и стандартное отклонение сигнала является стандартным отклонением ответов, разделенных на квадратный корень из 2. Начальное значение по умолчанию для параметра смеси шкалы равняется 1. Таким образом, phi = [std(X)';1;std(y)/sqrt(2)] |
| Указатель на функцию | r-by-1 вектор как начальное значение неограниченного вектора параметра phi поскольку пользовательское ядро функционирует kfcn. Когда KernelFunction указатель на функцию, необходимо предоставить начальные значения для параметров ядра. |
Для получения дополнительной информации о функциях ядра смотрите Ядро (Ковариация) Опции Функции.
Пример: 'KernelParameters',theta
Типы данных: double
DistanceMethod — Метод для вычисления разделяет расстояния знаками препинания'fast' (значение по умолчанию) | 'accurate'Метод для вычисления разделяет расстояния знаками препинания, чтобы выполнить встроенные функции ядра в виде любого 'fast' или 'accurate'. fitrgp вычисляет как когда вы выбираете fast опция и как когда вы выбираете accurate опция.
Пример: 'DistanceMethod','accurate'
ActiveSet — Наблюдения в активном наборе[] (значение по умолчанию) | m-by-1 вектор из целых чисел в пределах от 1 к n (m ≤ n) | логический вектор из длины nНаблюдения в активном наборе в виде m-by-1 вектор из целых чисел в пределах от 1 к n (m ≤ n) или логический вектор из длины n по крайней мере с одним true элемент. n является общим количеством наблюдений в обучающих данных.
fitrgp использует наблюдения, обозначенные ActiveSet обучать модель GPR. Активный набор не может иметь дублирующихся элементов.
Если вы предоставляете ActiveSetто:
fitrgp не использует ActiveSetSize и ActiveSetMethod.
Вы не можете выполнить перекрестную проверку на этой модели.
Типы данных: double | logical
ActiveSetSize — Размер активного набора для разреженных методовРазмер активного набора для разреженных методов ('sd', 'sr', 'fic') в виде целочисленного m, 1 ≤ m ≤ n, где n является количеством наблюдений.
Значением по умолчанию является min (1000, n) когда FitMethod 'sr' или 'fic', и min (2000, n), в противном случае.
Пример: 'ActiveSetSize',100
Типы данных: double
ActiveSetMethod — Активный метод выбора набора'random' (значение по умолчанию) | 'sgma' | 'entropy' | 'likelihood'Активный метод выбора набора в виде одного из следующих.
| Метод | Описание |
|---|---|
'random' | Случайный выбор |
'sgma' | Разреженное жадное матричное приближение |
'entropy' | Дифференциальный основанный на энтропии выбор |
'likelihood' | Подмножество регрессоров регистрирует основанный на вероятности выбор |
Все активные методы выбора набора (кроме 'random') потребуйте устройства хранения данных n-by-m матрица, где m является размером активного набора, и n является количеством наблюдений.
Пример: 'ActiveSetMethod','entropy'
RandomSearchSetSize — Случайный поисковый размер набораСлучайный поисковый размер набора на жадное включение для активного выбора набора в виде целочисленного значения.
Пример: 'RandomSearchSetSize',30
Типы данных: double
ToleranceActiveSet — Относительная погрешность для завершения активного выбора набораОтносительная погрешность для завершения активного выбора набора в виде значения положительной скалярной величины.
Пример: 'ToleranceActiveset',0.0002
Типы данных: double
NumActiveSetRepeats — Количество повторенийКоличество повторений для чередованного активного выбора набора и оценки параметра, когда ActiveSetMethod не 'random'В виде целочисленного значения.
Пример: 'NumActiveSetRepeats',5
Типы данных: double
PredictMethod — Метод раньше делал предсказания'exact' | 'bcd' | 'sd' | 'sr' | 'fic'Метод раньше делал предсказания из Гауссовой модели процесса, учитывая параметры в виде одного из следующих.
| Метод | Описание |
|---|---|
'exact' | Точный Гауссов метод регрессии процесса. Значение по умолчанию, если n ≤ 10000. |
'bcd' | Блокируйте координатный спуск. Значение по умолчанию, если n> 10000. |
'sd' | Подмножество приближения точек данных. |
'sr' | Подмножество приближения регрессоров. |
'fic' | Полностью независимое условное приближение. |
Пример: 'PredictMethod','bcd'
BlockSizeBCD — Размер блокаРазмер блока для блока координирует метод спуска ('bcd') в виде целого числа в диапазоне от 1 до n, где n является количеством наблюдений.
Пример: 'BlockSizeBCD',1500
Типы данных: double
NumGreedyBCD — Количество жадных выборовBlockSizeBCD (значение по умолчанию) | целочисленное значение в диапазоне от 1 до BlockSizeBCDКоличество жадных выборов для блока координирует метод спуска ('bcd') в виде целого числа в диапазоне от 1 до BlockSizeBCD.
Пример: 'NumGreedyBCD',150
Типы данных: double
ToleranceBCD — Относительная погрешность на норме градиента1e-3 (значение по умолчанию) | положительная скалярная величинаОтносительная погрешность на норме градиента для завершения блока координирует метод спуска ('bcd') итерации в виде положительной скалярной величины.
Пример: 'ToleranceBCD',0.002
Типы данных: double
StepToleranceBCD — Абсолютная погрешность на размере шага1e-3 (значение по умолчанию) | положительная скалярная величинаАбсолютная погрешность на размере шага для завершения блока координирует метод спуска ('bcd') итерации в виде положительной скалярной величины.
Пример: 'StepToleranceBCD',0.002
Типы данных: double
IterationLimitBCD — Максимальное количество итераций BCDМаксимальное количество блока координирует метод спуска ('bcd') итерации в виде целочисленного значения.
Пример: 'IterationLimitBCD',10000
Типы данных: double
Optimizer — Оптимизатор, чтобы использовать для оценки параметра'quasinewton' (значение по умолчанию) | 'lbfgs' | 'fminsearch' | 'fminunc' | 'fmincon'Оптимизатор, чтобы использовать для оценки параметра в виде одного из значений в этой таблице.
| Значение | Описание |
|---|---|
'quasinewton' | Плотный, симметричный rank-1-based, приближение квазиньютона к Гессиану |
'lbfgs' | Основанное на LBFGS приближение квазиньютона к Гессиану |
'fminsearch' | Неограниченная нелинейная оптимизация с помощью симплексного метода поиска Lagarias и др. [5] |
'fminunc' | Неограниченная нелинейная оптимизация (требует лицензии Optimization Toolbox™), |
'fmincon' | Ограниченная нелинейная оптимизация (требует лицензии Optimization Toolbox), |
Для получения дополнительной информации об оптимизаторах см. Алгоритмы.
Пример: 'Optimizer','fmincon'
OptimizerOptions — Опции для оптимизатораОпции для оптимизатора вы выбираете использование Optimizer аргумент пары "имя-значение" в виде структуры или объекта создается optimset, statset('fitrgp'), или optimoptions.
| Оптимизатор | Создайте опции оптимизатора Используя |
|---|---|
'fminsearch' | optimset Структура |
'quasinewton' или 'lbfgs' | statset('fitrgp') Структура |
'fminunc' или 'fmincon' | optimoptions объект |
Опции по умолчанию зависят от типа оптимизатора.
Пример: 'OptimizerOptions',opt
InitialStepSize — Начальный размер шага[] (значение по умолчанию) | действительная положительная скалярная величина | 'auto'Начальный размер шага в виде действительной положительной скалярной величины или 'auto'.
'InitialStepSize' аппроксимированное максимальное абсолютное значение первого шага оптимизации, когда оптимизатором является 'quasinewton' или 'lbfgs'. Начальный размер шага может определить начальное приближение Гессиана во время оптимизации.
По умолчанию, fitrgp не использует начальный размер шага, чтобы определить начальное приближение Гессиана. Чтобы использовать начальный размер шага, установите значение для 'InitialStepSize' аргумент пары "имя-значение", или задают 'InitialStepSize','auto' иметь fitrgp определите значение автоматически. Для получения дополнительной информации о 'auto', см. Алгоритмы.
Пример: 'InitialStepSize','auto'
CrossVal — Индикатор для перекрестной проверки'off' (значение по умолчанию) | 'on' Индикатор для перекрестной проверки в виде любого 'off' или 'on'. Если это - 'on', затем fitrgp возвращает модель GPR, перекрестную подтвержденную с 10 сгибами.
Можно использовать один из KFold, Holdout, Leaveout или CVPartition аргументы пары "имя-значение", чтобы изменить настройки перекрестной проверки по умолчанию. Можно использовать только одну из этих пар "имя-значение" за один раз.
Как альтернатива, можно использовать crossval метод для вашей модели.
Пример: 'CrossVal','on'
CVPartition — Случайный раздел для стратифицированного k - сворачивает перекрестную проверкуcvpartition объектHoldout — Часть данных, чтобы использовать для тестированияЧасть данных, чтобы использовать для тестирования в валидации затяжки в виде скалярного значения в диапазоне от 0 до 1. Если вы задаете 'Holdout',p, затем программное обеспечение:
1. Случайным образом резервы вокруг p *100% данных как данные о валидации, и обучают модель с помощью остальной части данных
2. Хранит компактную, обученную модель в cvgprMdl.Trained.
Пример: 'Holdout', 0.3 использование 30% данных для тестирования и 70% данных для обучения.
Если вы задаете Holdout, затем вы не можете задать CVPartition, KFold, или Leaveout.
Типы данных: double
KFold — Количество сгибовКоличество сгибов, чтобы использовать в перекрестной подтвержденной модели GPR в виде положительного целочисленного значения. KFold должен быть больше 1. Если вы задаете 'KFold',k затем программное обеспечение:
1. Случайным образом делит данные в наборы k.
2. Для каждого набора, резервирует набор как тестовые данные и обучает модель с помощью другого k – 1 набор.
3. Хранит k компактные, обученные модели в ячейках k-by-1 массив ячеек в cvgprMdl.Trained.
Пример: 'KFold',5 использование 5 сгибов в перекрестной проверке. Таким образом, для каждого сгиба, использование, которое сворачивается как тестовые данные и обучает модель на остающихся 4 сгибах.
Если вы задаете KFold, затем вы не можете задать CVPartition, Holdout, или Leaveout.
Типы данных: double
Leaveout — Индикатор для перекрестной проверки "пропускает один"'off' (значение по умолчанию) | 'on'Индикатор для перекрестной проверки "пропускает один" в виде любого 'off' или 'on'.
Если вы задаете 'Leaveout','on', затем, для каждого из наблюдений n, программного обеспечения:
1. Резервирует наблюдение как тестовые данные и обучает модель с помощью другого n – 1 наблюдение.
2. Хранит компактную, обученную модель в ячейке в n-by-1 массив ячеек cvgprMdl.Trained.
Пример: 'Leaveout','on'
Если вы задаете Leaveout, затем вы не можете задать CVPartition, Holdout, или KFold.
OptimizeHyperparameters — Параметры, чтобы оптимизировать'none' (значение по умолчанию) | 'auto' | 'all' | массив строк или массив ячеек имеющих право названий параметра | вектор из optimizableVariable объектыПараметры, чтобы оптимизировать в виде одного из следующего:
'none' — Не оптимизировать.
'auto' — Используйте {'Sigma'}.
'all' — Оптимизируйте все имеющие право параметры, эквивалентный to{'BasisFunction','KernelFunction','KernelScale','Sigma','Standardize'}.
Массив строк или массив ячеек имеющих право названий параметра.
Вектор из optimizableVariable объекты, обычно выход hyperparameters.
Оптимизация пытается минимизировать потерю перекрестной проверки (ошибка) для fitrgp путем варьирования параметров. Чтобы управлять типом перекрестной проверки и другими аспектами оптимизации, используйте HyperparameterOptimizationOptions пара "имя-значение".
Примечание
Значения 'OptimizeHyperparameters' замените любые значения, вы задаете использование других аргументов name-value. Например, установка 'OptimizeHyperparameters' к 'auto' причины fitrgp оптимизировать гиперпараметры, соответствующие 'auto' опция и проигнорировать любые заданные значения для гиперпараметров.
Имеющие право параметры для fitrgp :
BasisFunction — fitrgp поисковые запросы среди 'constant''none', 'linear', и 'pureQuadratic'.
KernelFunction — fitrgp поисковые запросы среди 'ardexponential', 'ardmatern32', 'ardmatern52', 'ardrationalquadratic', 'ardsquaredexponential', 'exponential', 'matern32', 'matern52', 'rationalquadratic', и 'squaredexponential'.
KernelScale — fitrgp использует KernelParameters аргумент, чтобы задать значение масштабного коэффициента ядра, который считается постоянный во время подбора кривой. В этом случае все входные размерности ограничиваются иметь тот же KernelScale значение. fitrgp поисковые запросы среди вещественного значения в области значений [1e-3*MaxPredictorRange,MaxPredictorRange], где
MaxPredictorRange = max(max(X) - min(X)).
KernelScale не может быть оптимизирован ни для одного из ядер ARD.
Sigma — fitrgp поисковые запросы среди вещественного значения в области значений [1e-4, max(1e-3,10*ResponseStd)], где
ResponseStd = std(y).
Внутренне, fitrgp устанавливает ConstantSigma пара "имя-значение" к true так значение Sigma является постоянным во время подбора кривой.
Standardize — fitrgp поисковые запросы среди true и false.
Установите параметры не по умолчанию путем передачи вектора из optimizableVariable объекты, которые имеют значения не по умолчанию. Например,
load fisheriris params = hyperparameters('fitrgp',meas,species); params(1).Range = [1e-4,1e6];
Передайте params как значение OptimizeHyperparameters.
По умолчанию итеративное отображение появляется в командной строке, и графики появляются согласно количеству гиперпараметров в оптимизации. Для оптимизации и графиков, целевая функция является журналом (1 + потеря перекрестной проверки). Чтобы управлять итеративным отображением, установите Verbose поле 'HyperparameterOptimizationOptions' аргумент значения имени. Чтобы управлять графиками, установите ShowPlots поле 'HyperparameterOptimizationOptions' аргумент значения имени.
Для примера смотрите, Оптимизируют Регрессию GPR.
Пример: 'auto'
HyperparameterOptimizationOptions — Опции для оптимизацииОпции для оптимизации в виде структуры. Этот аргумент изменяет эффект OptimizeHyperparameters аргумент значения имени. Все поля в структуре являются дополнительными.
| Имя поля | Значения | Значение по умолчанию |
|---|---|---|
Optimizer |
| 'bayesopt' |
AcquisitionFunctionName |
Захват функционирует, чьи имена включают | 'expected-improvement-per-second-plus' |
MaxObjectiveEvaluations | Максимальное количество оценок целевой функции. | 30'bayesopt' и 'randomsearch', и целая сетка для 'gridsearch' |
MaxTime | Ограничение по времени в виде положительного действительного скаляра. Ограничение по времени находится в секундах, как измерено | Inf |
NumGridDivisions | Для 'gridsearch', количество значений в каждой размерности. Значение может быть вектором из положительных целых чисел, дающих количество значений для каждой размерности или скаляр, который применяется ко всем размерностям. Это поле проигнорировано для категориальных переменных. | 10 |
ShowPlots | Логическое значение, указывающее, показать ли графики. Если true, это поле строит лучшее наблюдаемое значение целевой функции против номера итерации. Если вы используете Байесовую оптимизацию (Optimizer 'bayesopt'), затем это поле также строит лучшее предполагаемое значение целевой функции. Лучшие наблюдаемые значения целевой функции и лучше всего оцененные значения целевой функции соответствуют значениям в BestSoFar (observed) и BestSoFar (estim.) столбцы итеративного отображения, соответственно. Можно найти эти значения в свойствах ObjectiveMinimumTrace и EstimatedObjectiveMinimumTrace из Mdl.HyperparameterOptimizationResults. Если проблема включает один или два параметра оптимизации для Байесовой оптимизации, то ShowPlots также строит модель целевой функции против параметров. | true |
SaveIntermediateResults | Логическое значение, указывающее, сохранить ли результаты когда Optimizer 'bayesopt'. Если true, это поле перезаписывает переменную рабочей области под названием 'BayesoptResults' в каждой итерации. Переменной является BayesianOptimization объект. | false |
Verbose | Отображение в командной строке:
Для получения дополнительной информации смотрите | 1 |
UseParallel | Логическое значение, указывающее, запустить ли Байесовую оптимизацию параллельно, которая требует Parallel Computing Toolbox™. Из-за невоспроизводимости синхронизации параллели, параллельная Байесова оптимизация не обязательно приводит к восстанавливаемым результатам. Для получения дополнительной информации смотрите Параллельную Байесовую Оптимизацию. | false |
Repartition | Логическое значение, указывающее, повторно разделить ли перекрестную проверку в каждой итерации. Если этим полем является Установка | false |
| Используйте не больше, чем одну из следующих трех опций. | ||
CVPartition | cvpartition объект, как создано cvpartition | 'Kfold',5 если вы не задаете поле перекрестной проверки |
Holdout | Скаляр в области значений (0,1) представление части затяжки | |
Kfold | Целое число, больше, чем 1 | |
Пример: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)
Типы данных: struct
PredictorNames — Имена переменного предиктораПеременный предиктор называет в виде массива строк уникальных имен или массива ячеек уникальных векторов символов. Функциональность 'PredictorNames' зависит от способа, которым вы снабжаете обучающими данными.
Если вы предоставляете X и y, затем можно использовать 'PredictorNames' дать переменные предикторы в X имена.
Порядок имен в PredictorNames должен соответствовать порядку следования столбцов X. Таким образом, PredictorNames{1} имя X(:,1), PredictorNames{2} имя X(:,2), и так далее. Кроме того, size(X,2) и numel(PredictorNames) должно быть равным.
По умолчанию, PredictorNames {'x1','x2',...}.
Если вы предоставляете Tbl, затем можно использовать 'PredictorNames' выбрать который переменные предикторы использовать в обучении. Таким образом, fitrgp использует переменные предикторы в PredictorNames и ответ только в обучении.
PredictorNames должно быть подмножество Tbl.Properties.VariableNames и не может включать имя переменной отклика.
По умолчанию, PredictorNames содержит имена всех переменных предикторов.
Это хорошая практика, чтобы задать предикторы для обучения с помощью одного из 'PredictorNames' или formula только.
Пример: 'PredictorNames',{'PedalLength','PedalWidth'}
Типы данных: string | cell
ResponseName — Имя переменной отклика"Y" (значение по умолчанию) | вектор символов | строковый скалярИмя переменной отклика в виде вектора символов или строкового скаляра.
Если вы предоставляете Y, затем можно использовать ResponseName задавать имя для переменной отклика.
Если вы предоставляете ResponseVarName или formula, затем вы не можете использовать ResponseName.
Пример: "ResponseName","response"
Типы данных: char | string
Verbose — Уровень многословияУровень многословия в виде одного из следующих.
0 — fitrgp подавляет диагностические сообщения, связанные с активным выбором набора и спуском координаты блока, но отображает сообщения, связанные с оценкой параметра, в зависимости от значения 'Display' в OptimizerOptions.
1 — fitrgp отображает итеративные диагностические сообщения, связанные с оценкой параметра, активным выбором набора и спуском координаты блока.
Пример: 'Verbose',1
CacheSize — Размер кэша в мегабайтахРазмер кэша в мегабайтах (МБ) в виде положительной скалярной величины. Размер кэша является дополнительной памятью, которая доступна в дополнение к требуемому для подбора кривой и активного выбора набора. fitrgp использование CacheSize к:
Решите, разделяют ли расстояния знаками препинания, должен кэшироваться при оценке параметров.
Решите, как матричные векторные произведения должны быть вычислены для метода спуска координаты блока и для того, чтобы сделать предсказания.
Пример: 'CacheSize',2000
Типы данных: double
gprMdl — Гауссова модель регрессии процессаRegressionGP возразите | RegressionPartitionedModel объектГауссова модель регрессии процесса, возвращенная как RegressionGP или RegressionPartitionedModel объект.
Если вы перекрестный подтверждаете, то есть, если вы используете один из 'Crossval', 'KFold', 'Holdout', 'Leaveout', или 'CVPartition' аргументы name-value, затем gprMdl RegressionPartitionedModel объект. Можно использовать kfoldPredict предсказать ответы для наблюдений это fitrgp протягивает во время обучения. kfoldPredict предсказывает ответ для каждого наблюдения при помощи модели, обученной без того наблюдения. Вы не можете вычислить интервалы предсказания для перекрестной подтвержденной модели.
Если вы не перекрестный подтверждаете, то gprMdl RegressionGP объект. Можно использовать predict предсказать ответы для новых наблюдений и использования resubPredict предсказать ответы для учебных наблюдений. Можно также вычислить интервалы предсказания при помощи predict и resubPredict.
Для подмножества данных, подмножества регрессоров или полностью независимого условного приближения подходящие методы (FitMethod равняйтесь 'sd', 'sr', или 'fic'), если вы не обеспечиваете активный набор (или стимулирование входа установило), fitrgp выбирает активный набор и вычисляет оценки параметра в серии итераций.
В первой итерации программное обеспечение использует начальные значения параметров в векторном η 0 = [β 0, σ 0, θ 0], чтобы выбрать активный набор A1. Это максимизирует GPR крайняя логарифмическая вероятность или ее приближение с помощью η0 как начальные значения и A1, чтобы вычислить новые оценки параметра η1. Затем это вычисляет новую логарифмическую вероятность L 1 использование η1 и A1.
Во второй итерации программное обеспечение выбирает активный набор A2 с помощью значений параметров в η1. Затем с помощью η1 как начальные значения и A2, это максимизирует GPR крайняя логарифмическая вероятность или ее приближение и оценивает новые значения параметров η2. Затем с помощью η2 и A2, вычисляет новое логарифмическое значение вероятности L 2.
Следующая таблица обобщает итерации и что вычисляется в каждой итерации.
| Номер итерации | Активный набор | Вектор параметра | Регистрируйте вероятность |
|---|---|---|---|
| 1 | A1 | η1 | L 1 |
| 2 | A2 | η2 | L 2 |
| 3 | A3 | η3 | L 3 |
| … | … | … | … |
Программное обеспечение выполняет итерации так же для конкретного количества повторений. Можно задать количество репликаций для активного выбора набора с помощью NumActiveSetRepeats аргумент пары "имя-значение".
fitrgp принимает любую комбинацию подбора кривой, предсказания и активных методов выбора набора. В некоторых случаях не может быть возможно вычислить стандартные отклонения предсказанных ответов, следовательно интервалы предсказания. Смотрите predict. И в некоторых случаях, использование точного метода может быть дорогим из-за размера обучающих данных.
PredictorNames свойство хранит один элемент для каждого из исходных имен переменного предиктора. Например, если существует три предиктора, один из которых является категориальной переменной с тремя уровнями, PredictorNames 1 3 массив ячеек из символьных векторов.
ExpandedPredictorNames свойство хранит один элемент для каждого из переменных предикторов, включая фиктивные переменные. Например, если существует три предиктора, один из которых является категориальной переменной с тремя уровнями, затем ExpandedPredictorNames массив ячеек из символьных векторов 1 на 5.
Точно так же Beta свойство хранит один бета коэффициент для каждого предиктора, включая фиктивные переменные.
X свойство хранит обучающие данные, как первоначально введено. Это не включает фиктивные переменные.
Подход по умолчанию к инициализации приближения Гессиана в fitrgp может быть медленным, когда у вас есть модель GPR многими параметрами ядра, такой как тогда, когда с помощью ядра ARD со многими предикторами. В этом случае считайте определение 'auto' или значение для начального размера шага.
Можно установить 'Verbose',1 для отображения итеративных диагностических сообщений, и начинают обучение модель GPR с помощью LBFGS или оптимизатора квазиньютона со значением по умолчанию fitrgp оптимизация. Если итеративные диагностические сообщения не отображены после нескольких секунд возможно, что инициализация приближения Гессиана занимает слишком много времени. В этом случае полагайте, что обучение перезапуску и использование начального размера шага ускоряют оптимизацию.
После обучения модель можно сгенерировать код C/C++, который предсказывает ответы для новых данных. Генерация кода C/C++ требует MATLAB Coder™. Для получения дополнительной информации смотрите Введение в Генерацию кода..
Подбирать модель GPR включает оценку следующих параметров модели из данных:
Функция ковариации параметрированный в терминах параметров ядра в векторе (см. ядро (ковариация) опции функции),
Шумовое отклонение,
Вектор коэффициентов фиксированных основных функций,
Значение 'KernelParameters' аргументом пары "имя-значение" является вектор, который состоит из начальных значений для стандартного отклонения сигнала и характеристические шкалы расстояний . fitrgp функционируйте использует эти значения, чтобы определить параметры ядра. Точно так же 'Sigma' аргумент пары "имя-значение" содержит начальное значение для шумового стандартного отклонения .
Во время оптимизации, fitrgp создает вектор из неограниченных начальных значений параметров при помощи начальных значений для шумового стандартного отклонения и параметров ядра.
fitrgp аналитически определяет явные базисные коэффициенты , заданный 'Beta' аргумент пары "имя-значение", от ориентировочных стоимостей и . Поэтому не появляется в вектор, когда fitrgp инициализирует числовую оптимизацию.
Примечание
Если вы не задаете оценки параметров для модели GPR, fitrgp использует значение 'Beta' аргумент пары "имя-значение" и другие начальные значения параметров как известные значения параметров GPR (см. Beta). Во всех других случаях, значении 'Beta' аргумент оптимизирован аналитически от целевой функции.
Оптимизатор квазиньютона использует метод доверительной области с плотным, симметричным rank-1-based (SR1), приближением квазиньютона к Гессиану, в то время как оптимизатор LBFGS использует стандартный метод поиска линии приближением квазиньютона ограниченной памяти Бройдена Флетчера Голдфарба Шэнно (LBFGS) к Гессиану. Смотрите Носедэла и Райта [6].
Если вы устанавливаете 'InitialStepSize' аргумент пары "имя-значение" 'auto', fitrgp определяет начальный размер шага, , при помощи .
начальный вектор шага, и вектор из неограниченных начальных значений параметров.
Во время оптимизации, fitrgp использует начальный размер шага, , можно следующим образом:
Если вы используете 'Optimizer','quasinewton' с начальным размером шага затем начальное приближение Гессиана .
Если вы используете 'Optimizer','lbfgs' с начальным размером шага затем начальное приближение обратного Гессиана .
начальный вектор градиента, и единичная матрица.
[1] Нэш, W.J., Т. Л. Селлерс, С. Р. Тэлбот, А. Дж. Которн и В. Б. Форд. "Биология Населения Морского ушка (разновидности Haliotis) на Тасмании. I. Морское ушко Blacklip (H. rubra) от Северного Побережья и Островов Пролива Басса". Морское Деление Рыболовства, Технический отчет № 48, 1994.
[2] Во, S. "Расширяя и Тестируя Каскадной Корреляции в сравнении с эталоном: Расширения Архитектуры Каскадной Корреляции и Сравнительное тестирование Feedforward Контролируемые Искусственные Нейронные сети". Университет тезиса Факультета информатики Тасмании, 1995.
[3] Личмен, M. Репозиторий Машинного обучения UCI, Ирвин, CA: Калифорнийский университет, Школа Информатики и вычислительной техники, 2013. http://archive.ics.uci.edu/ml.
[4] Расмуссен, C. E. и К. К. Ай. Уильямс. Гауссовы процессы для машинного обучения. Нажатие MIT. Кембридж, Массачусетс, 2006.
[5] Lagarias, J. C. Дж. А. Ридс, М. Х. Райт и П. Э. Райт. "Свойства сходимости Симплекс-метода Nelder-меда в Низких Размерностях". SIAM Journal Оптимизации. Издание 9, Номер 1, 1998, стр 112–147.
[6] Nocedal, J. и С. Дж. Райт. Числовая оптимизация, второй выпуск. Ряд Спрингера в исследовании операций, Springer Verlag, 2006.
Чтобы выполнить параллельную гипероптимизацию параметров управления, используйте 'HyperparameterOptimizationOptions', struct('UseParallel',true) аргумент значения имени в вызове fitrgp функция.
Для получения дополнительной информации о параллельной гипероптимизации параметров управления смотрите Параллельную Байесовую Оптимизацию.
Для получения общей информации о параллельных вычислениях, смотрите функции MATLAB Запуска с Автоматической Параллельной Поддержкой (Parallel Computing Toolbox).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.