Скрытые модели Маркова (HMM)

Введение в Скрытые модели Маркова (HMM)

hidden Markov model (HMM) является тем, в котором вы наблюдаете последовательность эмиссии, но не знаете последовательность состояний, до которых пошла модель, генерируют эмиссию. Исследования скрытых моделей Маркова стремятся восстановить последовательность состояний из наблюдаемых данных.

Как пример, рассмотрите модель Маркова с двумя состояниями и шестью возможной эмиссией. Использование модели:

Красный умирает, имея шесть сторон, пометил 1 through 6.
Зеленый умирает, имея двенадцать сторон, пять из которых помечены 2 through 6, в то время как остающиеся семь сторон помечены 1.
Взвешенная красная монета, для которой вероятность голов.9 и вероятность хвостов.1.
Взвешенная зеленая монета, для которой вероятность голов.95 и вероятность хвостов.05.

Модель создает последовательность чисел из набора {1, 2, 3, 4, 5, 6} со следующими правилами:

Начните путем прокрутки красного, умирают и запись номера, который подходит, который является эмиссией.
Встряхните красную монету и выполните одно из следующих действий:
- Если результатом являются головы, прокрутитесь, красный умирают и записывают результат.
- Если результатом являются хвосты, прокрутитесь, зеленый умирают и записывают результат.
На каждом последующем шаге вы инвертируете монету, которая имеет тот же цвет как умирание, вы насыпали предыдущий шаг. Если монета подходит головы, прокрутитесь, то же самое умирают как на предыдущем шаге. Если монета подходит хвосты, переключатель к другому умирала.

Диаграмма состояний для этой модели имеет два состояния, красные и зеленые, как показано в следующем рисунке.

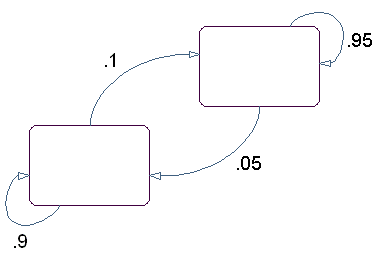
Вы определяете эмиссию состояния путем прокрутки умирания с тем же цветом как состояние. Вы определяете переход к следующему состоянию путем зеркального отражения монеты с тем же цветом как состояние.

Матрица перехода:

$T = [\begin{matrix} \begin{array}{l} 0.9 \\ 0.05 \end{array} & \begin{array}{l} 0.1 \\ 0.95 \end{array} \end{matrix}]$

Матрица эмиссии:

$E = [\begin{matrix} \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} \\ \frac{7}{12} & \frac{1}{12} & \frac{1}{12} & \frac{1}{12} & \frac{1}{12} & \frac{1}{12} \end{matrix}]$

Модель не скрыта, потому что вы знаете последовательность состояний от цветов монет и dice. Предположим, однако, что кто-то еще генерирует эмиссию, не показывая вам dice или монеты. Все, что вы видите, является последовательностью эмиссии. Если вы начинаете видеть больше 1 с, чем другие числа, вы можете подозревать, что модель находится в зеленом состоянии, но вы не можете быть уверены, потому что вы не видите, что цвет умирания прокручивается.

Скрытые модели Маркова поднимают следующие вопросы:

Учитывая последовательность эмиссии, каков наиболее вероятный путь состояния?
Учитывая последовательность эмиссии, как можно оценить вероятности перехода и эмиссии модели?
Какова прямая вероятность, что модель генерирует данную последовательность?
Какова апостериорная вероятность, что модель находится в конкретном состоянии в какой-либо точке в последовательности?

Анализ скрытых моделей Маркова

Генерация тестовой последовательности
Оценка последовательности состояния
Оценка матриц перехода и эмиссии
Оценка следующих вероятностей состояния
Изменение распределения начального состояния

Функции Statistics and Machine Learning Toolbox™, связанные со скрытыми моделями Маркова:

hmmgenerate — Генерирует последовательность состояний и выбросов модели Маркова
hmmestimate — Вычисляет оценки наибольшего правдоподобия вероятностей перехода и эмиссии от последовательности эмиссии и известной последовательности состояний
hmmtrain — Вычисляет оценки наибольшего правдоподобия вероятностей перехода и эмиссии от последовательности эмиссии
hmmviterbi — Вычисляет самый вероятный путь состояния для скрытой модели Маркова
hmmdecode — Вычисляет следующие вероятности состояния последовательности эмиссии

Этот раздел показывает, как использовать эти функции, чтобы анализировать скрытые модели Маркова.

Генерация тестовой последовательности

Следующие команды создают матрицы перехода и эмиссии для модели, описанной во Введении в Скрытые модели Маркова (HMM):

TRANS = [.9 .1; .05 .95];

EMIS = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6;...
7/12, 1/12, 1/12, 1/12, 1/12, 1/12];

Чтобы сгенерировать случайную последовательность состояний и выбросов модели, использовать hmmgenerate:

[seq,states] = hmmgenerate(1000,TRANS,EMIS);

Выход seq последовательность эмиссии и выхода states последовательность состояний.

hmmgenerate начинается в состоянии 1 на шаге 0, делает переход, чтобы утвердить i ₁ на шаге 1 и возвращает i ₁ как первая запись в states. Чтобы изменить начальное состояние, смотрите Изменение Распределения начального состояния.

Оценка последовательности состояния

Учитывая матрицы перехода и эмиссии TRANS и EMIS, функция hmmviterbi использует алгоритм Viterbi, чтобы вычислить наиболее вероятную последовательность состояний, до которых пошла бы модель, генерируют данную последовательность seq из эмиссии:

likelystates = hmmviterbi(seq, TRANS, EMIS);

likelystates последовательность та же длина как seq.

Протестировать точность hmmviterbi, вычислите процент фактической последовательности states это согласовывает с последовательностью likelystates.

sum(states==likelystates)/1000
ans =
   0.8200

В этом случае наиболее вероятная последовательность состояний согласовывает со случайной последовательностью 82% времени.

Функции hmmestimate и hmmtrain оцените матрицы перехода и эмиссии TRANS и EMIS учитывая последовательность seq из эмиссии.

Используя hmmestimate. Функция hmmestimate требует, чтобы вы знали последовательность состояний states то, что модель пошла до, генерируют seq.

Следующий берет эмиссию и последовательности состояния и возвращает оценки матриц перехода и эмиссии:

[TRANS_EST, EMIS_EST] = hmmestimate(seq, states)

TRANS_EST =
0.8989    0.1011
0.0585    0.9415

EMIS_EST =
0.1721    0.1721    0.1749    0.1612    0.1803    0.1393
0.5836    0.0741    0.0804    0.0789    0.0726    0.1104

Можно сравнить выходные параметры с исходными матрицами перехода и эмиссии, TRANS и EMIS:

TRANS
TRANS =
0.9000    0.1000
0.0500    0.9500

EMIS
EMIS =
0.1667    0.1667    0.1667    0.1667    0.1667    0.1667
0.5833    0.0833    0.0833    0.0833    0.0833    0.0833

Используя hmmtrain. Если вы не знаете последовательность состояний states, но у вас есть исходные предположения для TRANS и EMIS, можно все еще оценить TRANS и EMIS использование hmmtrain.

Предположим, что у вас есть следующие исходные предположения для TRANS и EMIS.

TRANS_GUESS = [.85 .15; .1 .9];
EMIS_GUESS = [.17 .16 .17 .16 .17 .17;.6 .08 .08 .08 .08 08];

Вы оцениваете TRANS и EMIS можно следующим образом:

[TRANS_EST2, EMIS_EST2] = hmmtrain(seq, TRANS_GUESS, EMIS_GUESS)

TRANS_EST2 =
0.2286    0.7714
0.0032    0.9968

EMIS_EST2 =
0.1436    0.2348    0.1837    0.1963    0.2350    0.0066
0.4355    0.1089    0.1144    0.1082    0.1109    0.1220

hmmtrain использует итеративный алгоритм, который изменяет матрицы TRANS_GUESS и EMIS_GUESS так, чтобы на каждом шаге настроенные матрицы, более вероятно, сгенерировали наблюдаемую последовательность, seq. Алгоритм останавливается, когда матрицы в двух последовательных итерациях в маленьком допуске друг друга.

Если алгоритму не удается достигнуть этого допуска в максимальном количестве итераций, значением по умолчанию которых является 100, остановы алгоритма. В этом случае, hmmtrain возвращает последние значения TRANS_EST и EMIS_EST и выдает предупреждение, что допуск не был достигнут.

Если алгоритму не удается достигнуть желаемого допуска, увеличить значение по умолчанию максимального количества итераций с командой:

hmmtrain(seq,TRANS_GUESS,EMIS_GUESS,'maxiterations',maxiter)

где maxiter максимальное количество шагов, которые выполняет алгоритм.

Измените значение по умолчанию допуска с командой:

hmmtrain(seq, TRANS_GUESS, EMIS_GUESS, 'tolerance', tol)

где tol требуемое значение допуска. Увеличение значения tol заставляет алгоритм остановиться раньше, но результаты менее точны.

Два фактора уменьшают надежность выходных матриц hmmtrain:

Алгоритм сходится к локальному максимуму, который не представляет истинные матрицы перехода и эмиссии. Если вы подозреваете это, используйте различные исходные предположения для матриц TRANS_EST и EMIS_EST.
Последовательность seq может быть слишком коротким, чтобы правильно обучить матрицы. Если вы подозреваете это, используйте более длинную последовательность для seq.

Оценка следующих вероятностей состояния

Следующие вероятности состояния последовательности эмиссии seq условные вероятности, что модель находится в конкретном состоянии, когда она генерирует символ в seq, учитывая, что seq испускается. Вы вычисляете следующие вероятности состояния с hmmdecode:

PSTATES = hmmdecode(seq,TRANS,EMIS)

Выход PSTATES M-by-L матрица, где M является количеством состояний, и L является длиной seq. PSTATES(i,j) условная вероятность, что модель находится в i состояния когда это генерирует jсимвол th seq, учитывая, что seq испускается.

hmmdecode начинается с модели в состоянии 1 на шаге 0, до первой эмиссии. PSTATES(i,1) вероятность, что модель находится в состоянии i в следующем шаге 1. Чтобы изменить начальное состояние, смотрите Изменение Распределения начального состояния.

Возвратить логарифм вероятности последовательности seq, используйте второй выходной аргумент hmmdecode:

[PSTATES,logpseq] = hmmdecode(seq,TRANS,EMIS)

Вероятность последовательности стремится к 0, когда длина последовательности увеличивается, и вероятность достаточно длинной последовательности становится меньше, чем самое маленькое положительное число, которое может представлять ваш компьютер. hmmdecode возвращает логарифм вероятности, чтобы избежать этой проблемы.

Изменение распределения начального состояния

По умолчанию Statistics and Machine Learning Toolbox скрытые функции модели Маркова начинается в состоянии 1. Другими словами, распределение начальных состояний имеет всю свою вероятностную меру, сконцентрированную в состоянии 1. Чтобы присвоить различное распределение вероятностей, p = [p ₁, p ₂..., p _M], к начальным состояниям M, делает следующее:

Создайте M, +1-by-M+1 увеличил матрицу перехода, $\hat{T}$ из следующей формы:
$\hat{T} = [\begin{matrix} 0 & p \\ 0 & T \end{matrix}]$
где T является истинной матрицей перехода. Первый столбец $\hat{T}$ содержит M +1 нуль. p должен суммировать к 1.
Создайте M, +1-by-N увеличил матрицу эмиссии, $\hat{E}$ , это имеет следующую форму:
$\hat{E} = [\begin{matrix} 0 \\ E \end{matrix}]$

Если матрицами перехода и эмиссии является TRANS и EMIS, соответственно, вы создаете увеличенные матрицы со следующими командами:

TRANS_HAT = [0 p; zeros(size(TRANS,1),1) TRANS];

EMIS_HAT = [zeros(1,size(EMIS,2)); EMIS];

Документация