Можно использовать машину опорных векторов (SVM), когда данные имеют точно два класса. SVM классифицирует данные путем нахождения лучшей гиперплоскости, которая разделяет все точки данных одного класса от тех из другого класса. Гиперплоскость best для SVM означает тот с самым большим margin между этими двумя классами. Поле означает максимальную ширину плиты, параллельной гиперплоскости, которая не имеет никаких внутренних точек данных.
support vectors является точками данных, которые являются самыми близкими к отделяющейся гиперплоскости; эти точки находятся на контуре плиты. Следующая фигура иллюстрирует эти определения, с + указание на точки данных типа 1, и – указание на точки данных типа-1.
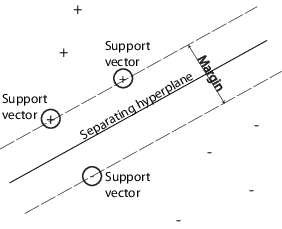
Математическая Формулировка: Основной. Это обсуждение следует за Hastie, Тибширэни и Фридманом [1] и Кристьанини и Шейв-Тейлор [2].
Данные для обучения являются набором точек (векторы) xj наряду с их категориями yj. Для некоторой размерности d, xj ∊ Rd, и yj = ±1. Уравнение гиперплоскости
где β ∊ Rd и b является вещественным числом.
Следующая проблема задает гиперплоскость разделения best (т.е. контур решения). Найдите β и b, которые минимизируют || β || таким образом это для всех точек данных (xj, yj),
Векторами поддержки является xj на контуре, тех для который
Для математического удобства проблема обычно дается как эквивалентная проблема минимизации . Это - проблема квадратичного программирования. Оптимальное решение включает классификацию векторного z можно следующим образом:
classification score и представляет расстояние, которое z от контура решения.
Математическая Формулировка: Двойной. В вычислительном отношении более просто решить двойную задачу квадратичного программирования. Чтобы получить двойное, возьмите положительные множители Лагранжа αj, умноженный на каждое ограничение, и вычтите из целевой функции:
где вы ищете стационарную точку LP по β и b. Устанавливая градиент LP к 0, вы добираетесь
| (1) |
Занимая место в LP, вы получаете двойной LD:
который вы максимизируете по αj ≥ 0. В общем случае многие αj 0 в максимуме. Ненулевой αj в решении двойной проблемы задает гиперплоскость, столь же замеченную в уравнении 1, которое дает β как сумма αjyjxj. Точками данных xj, соответствующий ненулевому αj, является support vectors.
Производная LD относительно ненулевого αj 0 в оптимуме. Это дает
В частности, это дает значение b в решении путем взятия любого j с ненулевым αj.
Двойной является стандартная проблема квадратичного программирования. Например, Optimization Toolbox™ quadprog (Optimization Toolbox) решатель решает этот тип проблемы.
Ваши данные не могут допускать отделяющуюся гиперплоскость. В этом случае SVM может использовать soft margin, означая гиперплоскость, которая разделяет многих, но не все точки данных.
Существует две стандартных формулировки мягких полей. Оба включают добавляющие слабые переменные ξj и параметр штрафа C.
L1- проблема нормы:
таким образом, что
L1- норма называет использование ξj слабыми переменными вместо их квадратов. Три опции решателя SMO, ISDA, и L1QP из fitcsvm минимизируйте L1- проблема нормы.
L2- проблема нормы:
подвергните тем же ограничениям.
В этих формулировках вы видите, что увеличение C помещает больше веса в слабые переменные ξj, означая попытки оптимизации сделать более строгое разделение между классами. Эквивалентно, сокращение C к 0 делает misclassification менее важный.
Математическая Формулировка: Двойной. Для более легких вычислений рассмотрите L1 двойная проблема к этой мягко-граничной формулировке. Используя множители Лагранжа μj, функция, чтобы минимизировать для L1- проблема нормы:
где вы ищете стационарную точку LP по β, b и положительному ξj. Устанавливая градиент LP к 0, вы добираетесь
Эти уравнения приводят непосредственно к двойной формулировке:
удовлетворяющее ограничениям
Итоговый набор неравенств, 0 ≤ αj ≤ C, показывает, почему C иногда называется box constraint. C сохраняет допустимые значения множителей Лагранжа αj в “поле”, ограниченной области.
Уравнение градиента для b дает решению b в терминах набора ненулевого αj, которые соответствуют векторам поддержки.
Можно записать и решить двойной из L2- проблема нормы аналогичным способом. Для получения дополнительной информации смотрите Кристьанини и Шейв-Тейлора [2], Глава 6.
fitcsvm Реализация. Обеими двойными мягко-граничными проблемами являются проблемы квадратичного программирования. Внутренне, fitcsvm имеет несколько различных алгоритмов для того, чтобы решить задачи.
Для или бинарной классификации одного класса, если вы не устанавливаете часть ожидаемых выбросов в данных (см. OutlierFraction), затем решатель по умолчанию является Последовательной минимальной оптимизацией (SMO). SMO минимизирует проблему с одной нормой рядом минимизаций 2D точки. Во время оптимизации SMO уважает линейное ограничение и явным образом включает член в модели смещения. SMO относительно быстр. Для получения дополнительной информации о SMO см. [3].
Для бинарной классификации, если вы устанавливаете часть ожидаемых выбросов в данных, затем решатель по умолчанию является Итеративным Одним Алгоритмом Данных. Как SMO, ISDA решает задачу с одной нормой. В отличие от SMO, ISDA минимизирует рядом на минимизациях с одной точкой, не уважает линейное ограничение и явным образом не включает член в модели смещения. Для получения дополнительной информации о ISDA см. [4].
Для или бинарной классификации одного класса, и если у вас есть лицензия Optimization Toolbox, можно принять решение использовать quadprog (Optimization Toolbox), чтобы решить задачу с одной нормой. quadprog использует большую память, но решает квадратичные программы в высокой степени точности. Для получения дополнительной информации см. Определение Квадратичного программирования (Optimization Toolbox).
Некоторые бинарные проблемы классификации не имеют простой гиперплоскости как полезного критерия разделения. Для тех проблем существует вариант математического подхода, который сохраняет почти всю простоту SVM разделение гиперплоскости.
Этот подход использует эти результаты теории репродуцирования ядер:
Существует класс функций G (x 1, x 2) со следующим свойством. Существует линейный пробел S и функциональный φ, сопоставляющий x с S, таким образом что
G (x 1, x 2) = <φ (x 1), φ (x 2)>.
Скалярное произведение происходит на пробеле S.
Этот класс функций включает:
Многочлены: Для некоторого положительного целочисленного p,
G (x 1, x 2) = (1 + x 1′x2)p.
Радиальная (Гауссова) основная функция:
G (x 1, x 2) = exp (– ∥x1–x2) ∥2).
Многоуровневый perceptron или сигмоидальный (нейронная сеть): Для положительного числа p 1 и отрицательное число p 2,
G (x 1, x 2) = tanh (p 1x1′x2 + p 2).
Примечание
Не каждый набор p 1 и p 2 выражения допустимое ядро репродуцирования.
fitcsvm не поддерживает сигмоидальное ядро. Вместо этого можно задать сигмоидальное ядро и задать его при помощи 'KernelFunction' аргумент пары "имя-значение". Для получения дополнительной информации смотрите, Обучают Классификатор SVM Используя Пользовательское Ядро.
Математический подход с помощью ядер использует вычислительный метод гиперплоскостей. Все вычисления для классификации гиперплоскостей используют не что иное как скалярные произведения. Поэтому нелинейные ядра могут использовать идентичные вычисления и алгоритмы решения, и получить классификаторы, которые нелинейны. Получившиеся классификаторы являются гиперповерхностями на некотором пробеле S, но пробел S не должен быть идентифицирован или исследован.
Как с любым контролируемая модель изучения, вы сначала обучаете машину опорных векторов, и затем пересекаетесь, подтверждают классификатор. Используйте обученную машину, чтобы классифицировать (предсказывают) новые данные. Кроме того, чтобы получить удовлетворительную прогнозирующую точность, можно использовать различные функции ядра SVM, и необходимо настроить параметры функций ядра.
Обучайтесь, и опционально пересекитесь, подтверждают, использование классификатора SVM fitcsvm. Наиболее распространенный синтаксис:
SVMModel = fitcsvm(X,Y,'KernelFunction','rbf',...
'Standardize',true,'ClassNames',{'negClass','posClass'});Входные параметры:
X — Матрица данных о предикторе, где каждая строка является одним наблюдением и каждым столбцом, является одним предиктором.
Y — Массив класса помечает каждой строкой, соответствующей значению соответствующей строки в XY может быть категориальное, символ, или массив строк, логический или числовой вектор или массив ячеек из символьных векторов.
KernelFunction — Значением по умолчанию является 'linear' для изучения 2D класса, которое разделяет данные гиперплоскостью. Значение 'gaussian' (или 'rbf') значение по умолчанию для изучения одного класса и задает, чтобы использовать Гауссово (или радиальная основная функция) ядро. Важный шаг, чтобы успешно обучить классификатор SVM должен выбрать соответствующую функцию ядра.
Standardize — Отметьте указание, должно ли программное обеспечение стандартизировать предикторы перед обучением классификатор.
ClassNames — Различает отрицательные и положительные классы или задает который классы включать в данные. Отрицательный класс является первым элементом (или строка символьного массива), например, 'negClass', и положительный класс является вторым элементом (или строка символьного массива), например, 'posClass'. ClassNames должен быть совпадающий тип данных как Y. Это - хорошая практика, чтобы задать имена классов, особенно если вы сравниваете эффективность различных классификаторов.
Получившаяся, обученная модель (SVMModel) содержит оптимизированные параметры из алгоритма SVM, позволяя вам классифицировать новые данные.
Для большего количества пар "имя-значение" можно использовать, чтобы управлять обучением, видеть fitcsvm страница с описанием.
Классифицируйте новые данные с помощью predict. Синтаксис для классификации новых данных с помощью обученного классификатора SVM (SVMModel):
[label,score] = predict(SVMModel,newX);
Итоговый вектор, label, представляет классификацию каждой строки в X. score n-by-2 матрица мягких баллов. Каждая строка соответствует строке в X, который является новым наблюдением. Первый столбец содержит оценки для наблюдений, классифицируемых на отрицательный класс, и второй столбец содержит наблюдения баллов, классифицируемые на положительный класс.
Чтобы оценить апостериорные вероятности, а не баллы, сначала передайте обученный классификатор SVM (SVMModel) к fitPosterior, который соответствует счету к функции преобразования апостериорной вероятности к баллам. Синтаксис:
ScoreSVMModel = fitPosterior(SVMModel,X,Y);
Свойство ScoreTransform из классификатора ScoreSVMModel содержит оптимальную функцию преобразования. Передайте ScoreSVMModel к predict. Вместо того, чтобы возвращать баллы, выходной аргумент score содержит апостериорные вероятности наблюдения, классифицируемого отрицательно (столбец 1 score) или положительный (столбец 2 scoreКласс.
Используйте 'OptimizeHyperparameters' аргумент пары "имя-значение" fitcsvm найти значения параметров, которые минимизируют потерю перекрестной проверки. Имеющими право параметрами является 'BoxConstraint', 'KernelFunction', 'KernelScale', 'PolynomialOrder', и 'Standardize'. Для примера смотрите, Оптимизируют Подгонку Классификатора Используя Байесовую Оптимизацию. В качестве альтернативы можно использовать bayesopt функция, как показано в Оптимизируют перекрестный Подтвержденный Классификатор Используя bayesopt. bayesopt функция позволяет большей гибкости настраивать оптимизацию. Можно использовать bayesopt функция, чтобы оптимизировать любые параметры, включая параметры, которые не имеют право оптимизировать, когда вы используете fitcsvm функция.
Можно также попытаться настроить параметры классификатора вручную согласно этой схеме:
Передайте данные fitcsvm, и набор аргумент пары "имя-значение" 'KernelScale','auto'. Предположим, что обученная модель SVM называется SVMModel. Программное обеспечение использует эвристическую процедуру, чтобы выбрать шкалу ядра. Эвристическая процедура использует подвыборку. Поэтому, чтобы воспроизвести результаты, установите seed случайных чисел с помощью rng перед обучением классификатор.
Крест подтверждает классификатор путем передачи его crossval. По умолчанию программное обеспечение проводит 10-кратную перекрестную проверку.
Передайте перекрестную подтвержденную модель SVM kfoldLoss оценить и сохранить ошибку классификации.
Переобучите классификатор SVM, но настройте 'KernelScale' и 'BoxConstraint' аргументы в виде пар имя-значение.
BoxConstraint — Одна стратегия состоит в том, чтобы попробовать геометрическую последовательность параметра ограничения поля. Например, примите 11 значений от 1e-5 к 1e5 на коэффициент 10. Увеличение BoxConstraint может сократить число векторов поддержки, но также и может увеличить учебное время.
KernelScale — Одна стратегия состоит в том, чтобы попробовать геометрическую последовательность параметра сигмы RBF, масштабируемого в исходной шкале ядра. Сделайте это:
Получая исходную шкалу ядра, например, ks, использование записи через точку: ks = SVMModel.KernelParameters.Scale.
Используйте в качестве новых факторов шкал ядра оригинала. Например, умножьте ks этими 11 значениями 1e-5 к 1e5, увеличение на коэффициент 10.
Выберите модель, которая дает к самой низкой ошибке классификации. Вы можете хотеть далее совершенствовать свои параметры, чтобы получить лучшую точность. Начните со своих начальных параметров и выполните другой шаг перекрестной проверки, на этот раз с помощью фактора 1,2.
В этом примере показано, как сгенерировать нелинейный классификатор с Гауссовой функцией ядра. Во-первых, сгенерируйте один класс точек в единичном диске в двух измерениях и другой класс точек в кольце от радиуса 1 к радиусу 2. Затем генерирует классификатор на основе данных с Гауссовым радиальным ядром основной функции. Линейный классификатор по умолчанию является очевидно неподходящим для этой проблемы, поскольку модель циркулярная симметричный. Установите параметр ограничения поля на Inf сделать строгую классификацию, не означая неправильно классифицированных учебных точек. Другие функции ядра не могут работать с этим строгим ограничением поля, поскольку они могут не мочь обеспечить строгую классификацию. Даже при том, что rbf классификатор может разделить классы, результат может быть перетренирован.
Сгенерируйте 100 точек, равномерно распределенных на единичном диске. Для этого сгенерируйте радиус r как квадратный корень из универсальной случайной переменной, сгенерируйте угол t однородно в (0, ), и помещенный точка в (r because(t), r sin (t)).
rng(1); % For reproducibility r = sqrt(rand(100,1)); % Radius t = 2*pi*rand(100,1); % Angle data1 = [r.*cos(t), r.*sin(t)]; % Points
Сгенерируйте 100 точек, равномерно распределенных в кольце. Радиус снова пропорционален квадратному корню, на этот раз квадратный корень из равномерного распределения от 1 до 4.
r2 = sqrt(3*rand(100,1)+1); % Radius t2 = 2*pi*rand(100,1); % Angle data2 = [r2.*cos(t2), r2.*sin(t2)]; % points
Постройте точки и постройте круги радиусов 1 и 2 для сравнения.
figure; plot(data1(:,1),data1(:,2),'r.','MarkerSize',15) hold on plot(data2(:,1),data2(:,2),'b.','MarkerSize',15) ezpolar(@(x)1);ezpolar(@(x)2); axis equal hold off

Поместите данные в одну матрицу и сделайте вектор из классификаций.
data3 = [data1;data2]; theclass = ones(200,1); theclass(1:100) = -1;
Обучите классификатор SVM с KernelFunction установите на 'rbf' и BoxConstraint установите на Inf. Постройте контур решения и отметьте векторы поддержки.
%Train the SVM Classifier cl = fitcsvm(data3,theclass,'KernelFunction','rbf',... 'BoxConstraint',Inf,'ClassNames',[-1,1]); % Predict scores over the grid d = 0.02; [x1Grid,x2Grid] = meshgrid(min(data3(:,1)):d:max(data3(:,1)),... min(data3(:,2)):d:max(data3(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(cl,xGrid); % Plot the data and the decision boundary figure; h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.'); hold on ezpolar(@(x)1); h(3) = plot(data3(cl.IsSupportVector,1),data3(cl.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'}); axis equal hold off

fitcsvm генерирует классификатор, который является близко к кругу радиуса 1. Различие происходит из-за случайных обучающих данных.
Обучение параметрами по умолчанию делает более близко круговой контур классификации, но тот, который неправильно классифицирует некоторые обучающие данные. Кроме того, значение по умолчанию BoxConstraint 1, и, поэтому, существует больше векторов поддержки.
cl2 = fitcsvm(data3,theclass,'KernelFunction','rbf'); [~,scores2] = predict(cl2,xGrid); figure; h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.'); hold on ezpolar(@(x)1); h(3) = plot(data3(cl2.IsSupportVector,1),data3(cl2.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'}); axis equal hold off

В этом примере показано, как использовать пользовательскую функцию ядра, такую как сигмоидальное ядро, чтобы обучить классификаторы SVM и настроить пользовательские параметры функции ядра.
Сгенерируйте случайный набор точек в модульном кругу. Пометьте точки в первых и третьих квадрантах как принадлежащий положительному классу и тем во вторых и четвертых квадрантах в отрицательном классе.
rng(1); % For reproducibility n = 100; % Number of points per quadrant r1 = sqrt(rand(2*n,1)); % Random radii t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3 X1 = [r1.*cos(t1) r1.*sin(t1)]; % Polar-to-Cartesian conversion r2 = sqrt(rand(2*n,1)); t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4 X2 = [r2.*cos(t2) r2.*sin(t2)]; X = [X1; X2]; % Predictors Y = ones(4*n,1); Y(2*n + 1:end) = -1; % Labels
Отобразите данные на графике.
figure;
gscatter(X(:,1),X(:,2),Y);
title('Scatter Diagram of Simulated Data')

Запишите функцию, которая принимает две матрицы в пространстве признаков как входные параметры и преобразовывает их в матрицу Грамма использование сигмоидального ядра.
function G = mysigmoid(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 1; c = -1; G = tanh(gamma*U*V' + c); end
Сохраните этот код как файл с именем mysigmoid на вашем пути MATLAB®.
Обучите классификатор SVM с помощью сигмоидальной функции ядра. Это - хорошая практика, чтобы стандартизировать данные.
Mdl1 = fitcsvm(X,Y,'KernelFunction','mysigmoid','Standardize',true);
Mdl1 ClassificationSVM классификатор, содержащий предполагаемые параметры.
Отобразите данные на графике и идентифицируйте векторы поддержки и контур решения.
% Compute the scores over a grid d = 0.02; % Step size of the grid [x1Grid,x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)),... min(X(:,2)):d:max(X(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; % The grid [~,scores1] = predict(Mdl1,xGrid); % The scores figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl1.IsSupportVector,1),... X(Mdl1.IsSupportVector,2),'ko','MarkerSize',10); % Support vectors contour(x1Grid,x2Grid,reshape(scores1(:,2),size(x1Grid)),[0 0],'k'); % Decision boundary title('Scatter Diagram with the Decision Boundary') legend({'-1','1','Support Vectors'},'Location','Best'); hold off

Можно настроить параметры ядра в попытке улучшить форму контура решения. Эта сила также уменьшает misclassification уровень в выборке, но, необходимо сначала определить misclassification уровень из выборки.
Определите misclassification уровень из выборки при помощи 10-кратной перекрестной проверки.
CVMdl1 = crossval(Mdl1); misclass1 = kfoldLoss(CVMdl1); misclass1
misclass1 =
0.1350
misclassification уровень из выборки составляет 13,5%.
Запишите другой сигмоидальной функции, но Набору gamma = 0.5;.
function G = mysigmoid2(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 0.5; c = -1; G = tanh(gamma*U*V' + c); end
Сохраните этот код как файл с именем mysigmoid2 на вашем пути MATLAB®.
Обучите другой классификатор SVM с помощью настроенного сигмоидального ядра. Отобразите на графике данные и область решения, и определите misclassification уровень из выборки.
Mdl2 = fitcsvm(X,Y,'KernelFunction','mysigmoid2','Standardize',true); [~,scores2] = predict(Mdl2,xGrid); figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl2.IsSupportVector,1),... X(Mdl2.IsSupportVector,2),'ko','MarkerSize',10); title('Scatter Diagram with the Decision Boundary') contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend({'-1','1','Support Vectors'},'Location','Best'); hold off CVMdl2 = crossval(Mdl2); misclass2 = kfoldLoss(CVMdl2); misclass2
misclass2 =
0.0450

После сигмоидальной наклонной корректировки новый контур решения, кажется, обеспечивает лучшую подгонку в выборке и контракты уровня перекрестной проверки больше чем на 66%.
В этом примере показано, как оптимизировать классификацию SVM с помощью fitcsvm функционируйте и OptimizeHyperparameters аргумент значения имени.
Сгенерируйте данные
Классификация работает над местоположениями точек от смешанной гауссовской модели. В Элементах Статистического Изучения, Hastie, Тибширэни и Фридмана (2009), страница 17 описывает модель. Модель начинается с генерации 10 базисных точек для "зеленого" класса, распределенного как 2D независимые нормали со средним значением (1,0) и модульное отклонение. Это также генерирует 10 базисных точек для "красного" класса, распределенного как 2D независимые нормали со средним значением (0,1) и модульное отклонение. Для каждого класса (зеленый и красный), сгенерируйте 100 случайных точек можно следующим образом:
Выберите базисную точку m соответствующего цвета однородно наугад.
Сгенерируйте независимую случайную точку с 2D нормальным распределением со средним значением m и отклонением I/5, где я - единичная матрица 2 на 2. В этом примере используйте отклонение I/50, чтобы показать преимущество оптимизации более ясно.
Сгенерируйте эти 10 базисных точек для каждого класса.
rng('default') % For reproducibility grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10);
Просмотрите базисные точки.
plot(grnpop(:,1),grnpop(:,2),'go') hold on plot(redpop(:,1),redpop(:,2),'ro') hold off

Поскольку некоторые красные базисные точки близко к зеленым базисным точкам, это может затруднить, чтобы классифицировать точки данных на основе одного только местоположения.
Сгенерируйте 100 точек данных каждого класса.
redpts = zeros(100,2); grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end
Просмотрите точки данных.
figure plot(grnpts(:,1),grnpts(:,2),'go') hold on plot(redpts(:,1),redpts(:,2),'ro') hold off

Подготовка данных для классификации
Поместите данные в одну матрицу и сделайте векторный grp это помечает класс каждой точки. 1 указывает, что зеленый класс, и –1 указывает на красный класс.
cdata = [grnpts;redpts]; grp = ones(200,1); grp(101:200) = -1;
Подготовьте перекрестную проверку
Настройте раздел для перекрестной проверки.
c = cvpartition(200,'KFold',10);Этот шаг является дополнительным. Если вы задаете раздел для оптимизации, то можно вычислить фактическую потерю перекрестной проверки для возвращенной модели.
Оптимизируйте подгонку
Найти хорошую подгонку, означая один оптимальными гиперпараметрами, которые минимизируют потерю перекрестной проверки, Байесовую оптимизацию использования. Задайте список гиперпараметров, чтобы оптимизировать при помощи OptimizeHyperparameters аргумент значения имени, и задает опции оптимизации при помощи HyperparameterOptimizationOptions аргумент значения имени.
Задайте 'OptimizeHyperparameters' как 'auto'. 'auto' опция включает типичный набор гиперпараметров, чтобы оптимизировать. fitcsvm находит оптимальные значения BoxConstraint и KernelScale. Установите опции гипероптимизации параметров управления использовать раздел перекрестной проверки c и выбрать 'expected-improvement-plus' функция захвата для воспроизводимости. Функция захвата по умолчанию зависит от времени выполнения и, поэтому, может дать различные результаты.
opts = struct('CVPartition',c,'AcquisitionFunctionName','expected-improvement-plus'); Mdl = fitcsvm(cdata,grp,'KernelFunction','rbf', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',opts)
|=====================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | | | result | | runtime | (observed) | (estim.) | | | |=====================================================================================================| | 1 | Best | 0.345 | 0.22192 | 0.345 | 0.345 | 0.00474 | 306.44 | | 2 | Best | 0.115 | 0.16686 | 0.115 | 0.12678 | 430.31 | 1.4864 | | 3 | Accept | 0.52 | 0.14285 | 0.115 | 0.1152 | 0.028415 | 0.014369 | | 4 | Accept | 0.61 | 0.14104 | 0.115 | 0.11504 | 133.94 | 0.0031427 | | 5 | Accept | 0.34 | 0.14998 | 0.115 | 0.11504 | 0.010993 | 5.7742 | | 6 | Best | 0.085 | 0.14041 | 0.085 | 0.085039 | 885.63 | 0.68403 | | 7 | Accept | 0.105 | 0.13736 | 0.085 | 0.085428 | 0.3057 | 0.58118 | | 8 | Accept | 0.21 | 0.13978 | 0.085 | 0.09566 | 0.16044 | 0.91824 | | 9 | Accept | 0.085 | 0.16771 | 0.085 | 0.08725 | 972.19 | 0.46259 | | 10 | Accept | 0.1 | 0.15169 | 0.085 | 0.090952 | 990.29 | 0.491 | | 11 | Best | 0.08 | 0.13653 | 0.08 | 0.079362 | 2.5195 | 0.291 | | 12 | Accept | 0.09 | 0.12055 | 0.08 | 0.08402 | 14.338 | 0.44386 | | 13 | Accept | 0.1 | 0.12305 | 0.08 | 0.08508 | 0.0022577 | 0.23803 | | 14 | Accept | 0.11 | 0.12852 | 0.08 | 0.087378 | 0.2115 | 0.32109 | | 15 | Best | 0.07 | 0.1381 | 0.07 | 0.081507 | 910.2 | 0.25218 | | 16 | Best | 0.065 | 0.1715 | 0.065 | 0.072457 | 953.22 | 0.26253 | | 17 | Accept | 0.075 | 0.18371 | 0.065 | 0.072554 | 998.74 | 0.23087 | | 18 | Accept | 0.295 | 0.14336 | 0.065 | 0.072647 | 996.18 | 44.626 | | 19 | Accept | 0.07 | 0.15007 | 0.065 | 0.06946 | 985.37 | 0.27389 | | 20 | Accept | 0.165 | 0.13721 | 0.065 | 0.071622 | 0.065103 | 0.13679 | |=====================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | | | result | | runtime | (observed) | (estim.) | | | |=====================================================================================================| | 21 | Accept | 0.345 | 0.12409 | 0.065 | 0.071764 | 971.7 | 999.01 | | 22 | Accept | 0.61 | 0.12674 | 0.065 | 0.071967 | 0.0010168 | 0.0010005 | | 23 | Accept | 0.345 | 0.12977 | 0.065 | 0.071959 | 0.0011459 | 995.89 | | 24 | Accept | 0.35 | 0.12457 | 0.065 | 0.071863 | 0.0010003 | 40.628 | | 25 | Accept | 0.24 | 0.18461 | 0.065 | 0.072124 | 996.55 | 10.423 | | 26 | Accept | 0.61 | 0.14087 | 0.065 | 0.072067 | 994.71 | 0.0010063 | | 27 | Accept | 0.47 | 0.13224 | 0.065 | 0.07218 | 993.69 | 0.029723 | | 28 | Accept | 0.3 | 0.12408 | 0.065 | 0.072291 | 993.15 | 170.01 | | 29 | Accept | 0.16 | 0.27101 | 0.065 | 0.072103 | 992.81 | 3.8594 | | 30 | Accept | 0.365 | 0.12737 | 0.065 | 0.072112 | 0.0010017 | 0.044287 |


__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 24.9814 seconds
Total objective function evaluation time: 4.4776
Best observed feasible point:
BoxConstraint KernelScale
_____________ ___________
953.22 0.26253
Observed objective function value = 0.065
Estimated objective function value = 0.073726
Function evaluation time = 0.1715
Best estimated feasible point (according to models):
BoxConstraint KernelScale
_____________ ___________
985.37 0.27389
Estimated objective function value = 0.072112
Estimated function evaluation time = 0.15739
Mdl =
ClassificationSVM
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [-1 1]
ScoreTransform: 'none'
NumObservations: 200
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
Alpha: [77x1 double]
Bias: -0.2352
KernelParameters: [1x1 struct]
BoxConstraints: [200x1 double]
ConvergenceInfo: [1x1 struct]
IsSupportVector: [200x1 logical]
Solver: 'SMO'
Properties, Methods
fitcsvm возвращает ClassificationSVM объект модели, который использует лучшую предполагаемую допустимую точку. Лучшая предполагаемая допустимая точка является набором гиперпараметров, который минимизирует верхнюю доверительную границу потери перекрестной проверки на основе базовой Гауссовой модели процесса Байесового процесса оптимизации.
Байесов процесс оптимизации внутренне обеспечивает Гауссову модель процесса целевой функции. Целевая функция является перекрестным подтвержденным misclassification уровнем для классификации. Для каждой итерации процесс оптимизации обновляет Гауссову модель процесса и использует модель, чтобы найти новый набор гиперпараметров. Каждая линия итеративного отображения показывает новый набор гиперпараметров и этих значений столбцов:
Objective — Значение целевой функции вычисляется в новом наборе гиперпараметров.
Objective runtime — Время оценки целевой функции.
Eval result — Отчет результата в виде Accept, Best, или Error. Accept указывает, что целевая функция возвращает конечное значение и Error указывает, что целевая функция возвращает значение, которое не является конечным действительным скаляром. Best указывает, что целевая функция возвращает конечное значение, которое ниже, чем ранее вычисленные значения целевой функции.
BestSoFar(observed) — Минимальное значение целевой функции вычисляется до сих пор. Это значение является любой значением целевой функции текущей итерации (если Eval result значением для текущей итерации является Best) или значение предыдущего Best итерация.
BestSoFar(estim.) — В каждой итерации программное обеспечение оценивает верхние доверительные границы значений целевой функции, с помощью обновленной Гауссовой модели процесса, во всех наборах гиперпараметров, которые попробовали до сих пор. Затем программное обеспечение выбирает точку с минимальной верхней доверительной границей. BestSoFar(estim.) значение является значением целевой функции, возвращенным predictObjective функция в минимальной точке.
График ниже итеративного отображения показывает BestSoFar(observed) и BestSoFar(estim.) значения синего и зеленого цвета, соответственно.
Возвращенный объект Mdl использует лучшую предполагаемую допустимую точку, то есть, набор гиперпараметров, который производит BestSoFar(estim.) значение в итоговой итерации на основе итоговой Гауссовой модели процесса.
Можно получить лучшую точку из HyperparameterOptimizationResults свойство или при помощи bestPoint функция.
Mdl.HyperparameterOptimizationResults.XAtMinEstimatedObjective
ans=1×2 table
BoxConstraint KernelScale
_____________ ___________
985.37 0.27389
[x,CriterionValue,iteration] = bestPoint(Mdl.HyperparameterOptimizationResults)
x=1×2 table
BoxConstraint KernelScale
_____________ ___________
985.37 0.27389
CriterionValue = 0.0888
iteration = 19
По умолчанию, bestPoint функционируйте использует 'min-visited-upper-confidence-interval' критерий. Этот критерий выбирает гиперпараметры, полученные из 19-й итерации как лучшая точка. CriterionValue верхняя граница перекрестной подтвержденной потери, вычисленной итоговой Гауссовой моделью процесса. Вычислите фактическую перекрестную подтвержденную потерю при помощи раздела c.
L_MinEstimated = kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,'KernelFunction','rbf', ... 'BoxConstraint',x.BoxConstraint,'KernelScale',x.KernelScale))
L_MinEstimated = 0.0700
Фактическая перекрестная подтвержденная потеря близко к ориентировочной стоимости. Estimated objective function value отображен ниже графиков результатов оптимизации.
Можно также извлечь лучшую наблюдаемую допустимую точку (то есть, последний Best укажите в итеративном отображении) от HyperparameterOptimizationResults свойство или путем определения Criterion как 'min-observed'.
Mdl.HyperparameterOptimizationResults.XAtMinObjective
ans=1×2 table
BoxConstraint KernelScale
_____________ ___________
953.22 0.26253
[x_observed,CriterionValue_observed,iteration_observed] = bestPoint(Mdl.HyperparameterOptimizationResults,'Criterion','min-observed')
x_observed=1×2 table
BoxConstraint KernelScale
_____________ ___________
953.22 0.26253
CriterionValue_observed = 0.0650
iteration_observed = 16
'min-observed' критерий выбирает гиперпараметры, полученные из 16-й итерации как лучшая точка. CriterionValue_observed вычисленное использование фактической перекрестной подтвержденной потери выбранных гиперпараметров. Для получения дополнительной информации смотрите аргумент значения имени Критерия bestPoint.
Визуализируйте оптимизированный классификатор.
d = 0.02; [x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)), ... min(cdata(:,2)):d:max(cdata(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(Mdl,xGrid); figure h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*'); hold on h(3) = plot(cdata(Mdl.IsSupportVector,1), ... cdata(Mdl.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'},'Location','Southeast');

Оцените точность на новых данных
Сгенерируйте и классифицируйте новые точки тестовых данных.
grnobj = gmdistribution(grnpop,.2*eye(2)); redobj = gmdistribution(redpop,.2*eye(2)); newData = random(grnobj,10); newData = [newData;random(redobj,10)]; grpData = ones(20,1); % green = 1 grpData(11:20) = -1; % red = -1 v = predict(Mdl,newData);
Вычислите misclassification уровни на наборе тестовых данных.
L_Test = loss(Mdl,newData,grpData)
L_Test = 0.3500
Определите, какие новые точки данных классифицируются правильно. Отформатируйте правильно классифицированные точки в красных квадратах и неправильно классифицированные точки в черных квадратах.
h(4:5) = gscatter(newData(:,1),newData(:,2),v,'mc','**'); mydiff = (v == grpData); % Classified correctly for ii = mydiff % Plot red squares around correct pts h(6) = plot(newData(ii,1),newData(ii,2),'rs','MarkerSize',12); end for ii = not(mydiff) % Plot black squares around incorrect pts h(7) = plot(newData(ii,1),newData(ii,2),'ks','MarkerSize',12); end legend(h,{'-1 (training)','+1 (training)','Support Vectors', ... '-1 (classified)','+1 (classified)', ... 'Correctly Classified','Misclassified'}, ... 'Location','Southeast'); hold off

В этом примере показано, как предсказать апостериорные вероятности моделей SVM по сетке наблюдений, и затем построить апостериорные вероятности по сетке. Графический вывод апостериорных вероятностей отсоединяет контуры решения.
Загрузите ирисовый набор данных Фишера. Обучите классификатор с помощью лепестковых длин и ширин, и удалите virginica разновидности из данных.
load fisheriris classKeep = ~strcmp(species,'virginica'); X = meas(classKeep,3:4); y = species(classKeep);
Обучите классификатор SVM с помощью данных. Это - хорошая практика, чтобы задать порядок классов.
SVMModel = fitcsvm(X,y,'ClassNames',{'setosa','versicolor'});
Оцените оптимальную функцию преобразования счета.
rng(1); % For reproducibility
[SVMModel,ScoreParameters] = fitPosterior(SVMModel); Warning: Classes are perfectly separated. The optimal score-to-posterior transformation is a step function.
ScoreParameters
ScoreParameters = struct with fields:
Type: 'step'
LowerBound: -0.8431
UpperBound: 0.6897
PositiveClassProbability: 0.5000
Оптимальная функция преобразования счета является ступенчатой функцией, потому что классы отделимы. Поля LowerBound и UpperBound из ScoreParameters укажите на более низкие и верхние конечные точки интервала баллов, соответствующих наблюдениям в разделяющих класс гиперплоскостях (поле). Никакое учебное наблюдение не находится в пределах поля. Если новый счет находится в интервале, то программное обеспечение присваивает соответствующее наблюдение положительная апостериорная вероятность класса, т.е. значение в PositiveClassProbability поле ScoreParameters.
Задайте сетку значений на наблюдаемом пробеле предиктора. Предскажите апостериорные вероятности для каждого экземпляра в сетке.
xMax = max(X); xMin = min(X); d = 0.01; [x1Grid,x2Grid] = meshgrid(xMin(1):d:xMax(1),xMin(2):d:xMax(2)); [~,PosteriorRegion] = predict(SVMModel,[x1Grid(:),x2Grid(:)]);
Постройте положительную область апостериорной вероятности класса и обучающие данные.
figure; contourf(x1Grid,x2Grid,... reshape(PosteriorRegion(:,2),size(x1Grid,1),size(x1Grid,2))); h = colorbar; h.Label.String = 'P({\it{versicolor}})'; h.YLabel.FontSize = 16; caxis([0 1]); colormap jet; hold on gscatter(X(:,1),X(:,2),y,'mc','.x',[15,10]); sv = X(SVMModel.IsSupportVector,:); plot(sv(:,1),sv(:,2),'yo','MarkerSize',15,'LineWidth',2); axis tight hold off

В изучении 2D класса, если классы отделимы, то существует три области: тот, где наблюдения имеют положительную апостериорную вероятность класса 0, тот, где это - 1, и другой, где это - положительная априорная вероятность класса.
В этом примере показано, как определить, какой квадрант изображения форма занимает по образованию модель выходных кодов с коррекцией ошибок (ECOC), состоявшую из линейных бинарных учеников SVM. Этот пример также иллюстрирует потребление дискового пространства моделей ECOC, которые хранят векторы поддержки, их метки и предполагаемое коэффициенты.
Создайте набор данных
Случайным образом поместите круг с радиусом пять в 50 50 изображение. Сделайте 5 000 изображений. Создайте метку для каждого изображения, указывающего на квадрант, который занимает круг. Квадрант 1 находится в верхнем правом углу, квадрант 2 находится в верхнем левом углу, квадрант 3 находится в нижнем левом углу, и квадрант 4 находится в нижнем правом углу. Предикторы являются интенсивностью каждого пикселя.
d = 50; % Height and width of the images in pixels n = 5e4; % Sample size X = zeros(n,d^2); % Predictor matrix preallocation Y = zeros(n,1); % Label preallocation theta = 0:(1/d):(2*pi); r = 5; % Circle radius rng(1); % For reproducibility for j = 1:n figmat = zeros(d); % Empty image c = datasample((r + 1):(d - r - 1),2); % Random circle center x = r*cos(theta) + c(1); % Make the circle y = r*sin(theta) + c(2); idx = sub2ind([d d],round(y),round(x)); % Convert to linear indexing figmat(idx) = 1; % Draw the circle X(j,:) = figmat(:); % Store the data Y(j) = (c(2) >= floor(d/2)) + 2*(c(2) < floor(d/2)) + ... (c(1) < floor(d/2)) + ... 2*((c(1) >= floor(d/2)) & (c(2) < floor(d/2))); % Determine the quadrant end
Постройте наблюдение.
figure imagesc(figmat) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant %d',Y(end)))

Обучите модель ECOC
Используйте 25%-ю выборку затяжки и задайте обучение и демонстрационные индексы затяжки.
p = 0.25; CVP = cvpartition(Y,'Holdout',p); % Cross-validation data partition isIdx = training(CVP); % Training sample indices oosIdx = test(CVP); % Test sample indices
Создайте шаблон SVM, который задает хранение векторов поддержки из бинарных учеников. Передайте его и обучающие данные к fitcecoc обучать модель. Определите ошибку классификации обучающих выборок.
t = templateSVM('SaveSupportVectors',true); MdlSV = fitcecoc(X(isIdx,:),Y(isIdx),'Learners',t); isLoss = resubLoss(MdlSV)
isLoss = 0
MdlSV обученный ClassificationECOC модель мультикласса. Это хранит обучающие данные и векторы поддержки из каждого бинарного ученика. Для больших наборов данных, таких как те в анализе изображения, модель может использовать большую память.
Определите сумму дискового пространства, которое использует модель ECOC.
infoMdlSV = whos('MdlSV');
mbMdlSV = infoMdlSV.bytes/1.049e6mbMdlSV = 763.6150
Модель использует 763,6 Мбайта.
Повысьте эффективность модели
Можно оценить эффективность из выборки. Можно также оценить, была ли модель сверхподходящей с уплотненной моделью, которая не содержит векторы поддержки, их связанные параметры и обучающие данные.
Отбросьте векторы поддержки и связанные параметры из обученной модели ECOC. Затем отбросьте обучающие данные из получившейся модели при помощи compact.
Mdl = discardSupportVectors(MdlSV); CMdl = compact(Mdl); info = whos('Mdl','CMdl'); [bytesCMdl,bytesMdl] = info.bytes; memReduction = 1 - [bytesMdl bytesCMdl]/infoMdlSV.bytes
memReduction = 1×2
0.0626 0.9996
В этом случае отбрасывание векторов поддержки уменьшает потребление памяти приблизительно на 6%. Уплотнение и отбрасывание векторов поддержки уменьшают размер приблизительно на 99,96%.
Альтернативный способ управлять векторами поддержки состоит в том, чтобы сократить их количество во время обучения путем определения большего ограничения поля, такой как 100. Хотя модели SVM, которые используют меньше векторов поддержки, более желательны и используют меньше памяти, увеличивание значения ограничения поля имеет тенденцию увеличивать учебное время.
Удалите MdlSV и Mdl из рабочей области.
clear Mdl MdlSV
Оцените демонстрационную эффективность затяжки
Вычислите ошибку классификации выборки затяжки. Постройте выборку демонстрационных предсказаний затяжки.
oosLoss = loss(CMdl,X(oosIdx,:),Y(oosIdx))
oosLoss = 0
yHat = predict(CMdl,X(oosIdx,:)); nVec = 1:size(X,1); oosIdx = nVec(oosIdx); figure; for j = 1:9 subplot(3,3,j) imagesc(reshape(X(oosIdx(j),:),[d d])) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant: %d',yHat(j))) end text(-1.33*d,4.5*d + 1,'Predictions','FontSize',17)

Модель не неправильно классифицирует демонстрационных наблюдений затяжки.
fitcsvm | bayesopt | kfoldLoss
[1] Hastie, T., Р. Тибширэни и Дж. Фридман. Элементы Статистического Изучения, второго выпуска. Нью-Йорк: Спрингер, 2008.
[2] Christianini, N. и Дж. Шейв-Тейлор. Введение в машины опорных векторов и другое основанное на ядре изучение методов. Кембридж, Великобритания: Издательство Кембриджского университета, 2000.
[3] Вентилятор, R.-E., P.-H. Чен и C.-J. Лин. “Выбор рабочего набора с помощью информации о втором порядке для учебных машин опорных векторов”. Журнал Исследования Машинного обучения, Vol 6, 2005, стр 1889–1918.
[4] Кекмен V, T.-M. Хуан и М. Вогт. “Итеративный Один Алгоритм Данных для Учебных Машин Ядра от Огромных Наборов данных: Теория и Эффективность”. В Машинах опорных векторов: Теория и Приложения. Отредактированный Липо Ваном, 255–274. Берлин: Springer-Verlag, 2005.