Exponenta Banner

dist

Угловое расстояние в радианах

свернуть все на странице

Синтаксис

distance = dist(quatA,quatB)

Описание

пример

distance = dist(quatA,quatB) возвращает угловое расстояние в радианах между двумя кватернионами, quatA и quatB.

Примеры

свернуть все

Скрипт Open Live Script

Вычислите расстояние кватерниона между одним кватернионом и каждым элементом вектора из кватернионов. Задайте кватернионы с помощью Углов Эйлера.

q = quaternion([0,0,0],'eulerd','zyx','frame')
q = quaternion
     1 + 0i + 0j + 0k


qArray = quaternion([0,45,0;0,90,0;0,180,0;0,-90,0;0,-45,0],'eulerd','zyx','frame')
qArray = 5x1 quaternion array
       0.92388 +         0i +   0.38268j +         0k
       0.70711 +         0i +   0.70711j +         0k
    6.1232e-17 +         0i +         1j +         0k
       0.70711 +         0i -   0.70711j +         0k
       0.92388 +         0i -   0.38268j +         0k


quaternionDistance = rad2deg(dist(q,qArray))
quaternionDistance = 5×1

   45.0000
   90.0000
  180.0000
   90.0000
   45.0000

Если оба аргумента к dist векторы, расстояние кватерниона вычисляется между соответствующими элементами. Вычислите расстояние кватерниона между двумя векторами кватерниона.

angles1 = [30,0,15; ...
           30,5,15; ...
           30,10,15; ...
           30,15,15];
angles2 = [30,6,15; ...
           31,11,15; ...
           30,16,14; ...
           30.5,21,15.5];

qVector1 = quaternion(angles1,'eulerd','zyx','frame');
qVector2 = quaternion(angles2,'eulerd','zyx','frame');

rad2deg(dist(qVector1,qVector2))
ans = 4×1

    6.0000
    6.0827
    6.0827
    6.0287

Обратите внимание на то, что кватернион представляет то же вращение как свое отрицание. Вычислите кватернион и его отрицание.

qPositive = quaternion([30,45,-60],'eulerd','zyx','frame')
qPositive = quaternion
     0.72332 - 0.53198i + 0.20056j +  0.3919k


qNegative = -qPositive
qNegative = quaternion
    -0.72332 + 0.53198i - 0.20056j -  0.3919k

Найдите расстояние между кватернионом и его отрицанием.

dist(qPositive,qNegative)
ans = 0

Компоненты кватерниона могут отличаться от компонентов его отрицания, но оба выражения представляют то же вращение.

Входные параметры

свернуть все

Кватернионы, чтобы вычислить расстояние между в виде разделенных от запятой кватернионов или массивов кватернионов. quatA и quatB должен иметь совместимые размеры:

  • size(quatA) == size(quatB), или

  • numel(quatA) == 1, или

  • numel(quatB) == 1, или

  • если [Adim1,…,AdimN] = size(quatA) и [Bdim1,…,BdimN] = size(quatB), затем для i = 1:N, любой Adimi==Bdimi или Adim==1 или Bdim==1.

    Если один из аргументов кватерниона содержит только один кватернион, то эта функция возвращает расстояния между тем кватернионом и каждым кватернионом в другом аргументе.

Типы данных: quaternion

Выходные аргументы

свернуть все

Угловое расстояние в радианах, возвращенных как массив. Размерности являются максимумом объединения size(quatA) и size(quatB).

Типы данных: single | double

Алгоритмы

dist функция возвращает угловое расстояние между двумя кватернионами.

Кватернион может быть задан осью (ub, uc, ud) и угол вращения θq: q=cos(θq2)+sin(θq2)(ubi+ucj+udk).

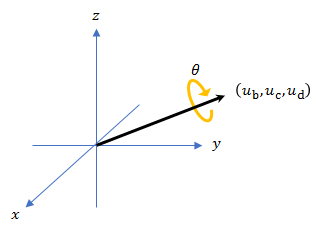
Angle Rotation

Учитывая кватернион в форме, q=a+bi+cj+dk, где a является действительной частью, можно решить для угла q как θq=2cos−1(a).

Рассмотрите два кватерниона, p и q и продукт z=p*conjugate(q). Когда p приближается к q, угол z переходит в 0, и z приближается к модульному кватерниону.

Угловое расстояние между двумя кватернионами может быть описано как θz=2cos−1(real(z)).

Используя quaternion синтаксис типа данных, угловое расстояние вычисляется как:

angularDistance = 2*acos(abs(parts(p*conj(q))));

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Функции

Объекты

Введенный в R2020b

Документация UAV Toolbox

Поддержка