Объединенное колесо промаха, совместимое с CPI стандарт Tydex
Vehicle Dynamics Blockset / Колеса и Шины
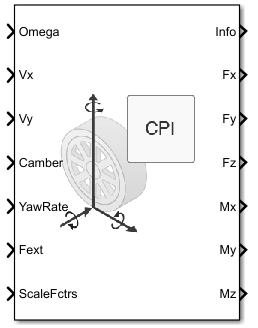

Блок Combined Slip Wheel CPI реализует продольное и боковое поведение колеса, охарактеризованного Волшебной Формулой1, 2 это выполняет Формат Обмена данными Шины интерфейса контактной точки (CPI) (TYDEX)3 стандарт. Можно импортировать собственные данные о шине или использование адаптированные наборы данных шины, обеспеченные Глобальным Центром Автомобильной Симуляции Эффективности (GCAPS). Используйте блок в автомобильной трансмиссии и симуляциях транспортного средства, где низкочастотные дорожные шиной взаимодействия требуются, чтобы определять ускорение транспортного средства, торможение и сопротивление качению колеса. Блок подходит для приложений, которые требуют объединенного бокового промаха, например, в боковом движении и исследованиях устойчивости рыскания.
На основе колеса вращательная скорость, продольная и поперечная скорость, угол изгиба колеса и давление инфляции, блок определяет вертикальное движение, силы, и моменты во всех шести степенях свободы (DOF). Используйте вертикальную степень свободы, чтобы изучить резонансы приостановки шины от дорожных профилей или движения шасси.
Используйте параметр Tire type, чтобы выбрать источник данных о шине.
| Цель | Действие |
|---|---|
Реализуйте Волшебную Формулу с помощью эмпирических уравнений1, 2. Подходящие коэффициенты использования уравнений, которые соответствуют параметрам блоков. | Обновите параметры блоков с подходящими коэффициентами из файла:
|
Реализуйте адаптированные наборы данных шины, обеспеченные Глобальным Центром Автомобильной Симуляции Эффективности (GCAPS). | Обновите применимые параметры блоков с GCAPS адаптированные данные о шине:
|
Блок вычисляет инерционный ответ колеса, удовлетворяющего:
Потери оси
Утомите сопротивление качению
Оснуйте контакт через дорожный шиной интерфейс
Чтобы реализовать Волшебную Формулу, блок использует эти уравнения.
| Вычисление | Уравнения |
|---|---|
Продольная сила | Шина и динамика аппарата2 уравнения 4. E9 до 4. E57 |
Боковая сила - чистый занос | Шина и динамика аппарата2 уравнения 4. E19 до 4. E30 |
Боковая сила - объединенный промах | Шина и динамика аппарата2 уравнения 4. E58 до 4. E67 |
Вертикальная динамика | Шина и динамика аппарата2 уравнения 4. E68, 4. E1, 4. E2a, и 4. 2 миллиарда евро |
Опрокидывание пары | Шина и динамика аппарата2 уравнение 4. E69 |
Сопротивление качению |
|
Выравнивание момента | Шина и динамика аппарата2 уравнение 4. E31 до 4. E49 |
Выравнивание крутящего момента - объединенный промах | Шина и динамика аппарата2 уравнение 4. E71 до 4. E78 |
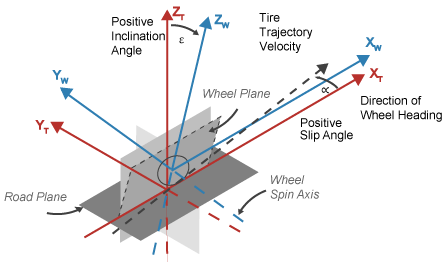
Использование блока утомляет оси системы координат (XT, YT, ZT), которые фиксируются в системе координат, присоединенной к шине. Источник в контакте шины с землей.
Систему координат шины CPI отображают красным.
Примечание
(Красная) система координат шины CPI эквивалентна системе координат оси колеса TYDEX.
[1]
| Ось | Описание |
|---|---|
| Xt | XT и YT параллельны дорожной плоскости. Пересечение плоскости колеса и дорожной плоскости задает ориентацию оси XT. |
| Yt | YT является проекцией оси вращения колеса на земле. |
| Zt | ZT указывает вверх. |
Omega — Вращательная скоростьscalar | N- 1 векторУтомите вращательную скорость, ω, об оси вращения колеса, в rad/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Vx — Продольная скоростьscalar | N- 1 векторОсь продольная скорость, Vx, вдоль зафиксированной шиной оси X, в m/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Vy — Поперечная скоростьscalar | N- 1 векторПоперечная скорость оси, Vy, вдоль зафиксированной шиной оси Y, в m/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Camber — Наклонный уголscalar | N- 1 векторУгол изгиба, ɣ, или наклонный угол, ε, в рад.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
YawRate — Утомите скорость вращенияscalar | N- 1 векторУтомите скорость вращения, r, о зафиксированной шиной оси z (уровень рыскания), в rad/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fext — Сила оси прикладывается к шинеscalar | N- 1 векторСила оси применялась к шине, Fext, вдоль зафиксированной транспортным средством оси z (положительный вход сжимает шину), в N.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
ScaleFctrs — Масштабные коэффициентыN массивВолшебный массив масштабного коэффициента Формулы. Измерениями массива является 27 количеством колес, N.
Уравнения Magic Formula используют масштабные коэффициенты с учетом статического или изменений времени выполнения симуляции. Номинально, большинство установлено в 1.
| Элемент массива | Переменная | ScaleFactor |
|---|---|---|
ScaleFctrs(1,1) | lam_Fzo | Номинальная загрузка |
ScaleFctrs(2,1) | lam_mux
| Продольный пиковый коэффициент трения |
ScaleFctrs(3,1) | lam_muy
| Боковой пиковый коэффициент трения |
ScaleFctrs(4,1) | lam_muV | Скорость скольжения, Vs, затухающее трение |
ScaleFctrs(5,1) | lam_Kxkappa
| Тормозите жесткость промаха |
ScaleFctrs(6,1) | lam_Kyalpha
| Движение на повороте жесткости |
ScaleFctrs(7,1) | lam_Cx | Продольный масштабный фактор |
ScaleFctrs(8,1) | lam_Cy | Боковой масштабный фактор |
ScaleFctrs(9,1) | lam_Ex
| Продольный фактор искривления |
ScaleFctrs(10,1) | lam_Ey
| Боковой фактор искривления |
ScaleFctrs(11,1) | lam_Hx
| Продольный горизонтальный сдвиг |
ScaleFctrs(12,1) | lam_Hy | Боковой горизонтальный сдвиг |
ScaleFctrs(13,1) | lam_Vx
| Продольный вертикальный сдвиг |
ScaleFctrs(14,1) | lam_Vy | Боковой вертикальный сдвиг |
ScaleFctrs(15,1) | lam_Kygamma
| Жесткость силы изгиба |
ScaleFctrs(16,1) | lam_Kzgamma | Жесткость крутящего момента изгиба |
ScaleFctrs(17,1) | lam_t | Пневматический след (производящий выравнивающий жесткость крутящего момента) |
ScaleFctrs(18,1) | lam_Mr | Остаточный крутящий момент |
ScaleFctrs(19,1) | lam_xalpha
| Альфа-влияние на Fx (каппа) |
ScaleFctrs(20,1) | lam_ykappa | Влияние каппы на Fy (альфа) |
ScaleFctrs(21,1) | lam_Vykappa
| Вызванный сгиб регулирует Fy |
ScaleFctrs(22,1) | lam_s
| Рука момента Fx |
ScaleFctrs(23,1) | lam_Cz
| Радиальная жесткость шины |
ScaleFctrs(24,1) | lam_Mx
| Опрокидывание жесткости пары |
ScaleFctrs(25,1) | lam_VMx
| Опрокидывание пары вертикальный сдвиг |
ScaleFctrs(26,1) | lam_My | Момент сопротивления качению |
ScaleFctrs(27,1) | lam_Mphi | Парковка крутящего момента Mz |
Prs — Давление накачивания шинscalar | N- 1 векторДавление накачивания шин, pi, в Па.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Чтобы создать этот порт, выберите Input tire pressure.
Info — Блокируйте данныеБлокируйте данные, возвращенные как сигнал шины, содержащий эти значения блока.
| Сигнал | Описание | Модули |
|---|---|---|
| Скорость вращения колеса о зафиксированной колесом оси Y | рад/с |
| Продольная сила транспортного средства вдоль зафиксированной шиной оси X | N |
| Боковая сила транспортного средства вдоль зафиксированной шиной оси Y | N |
| Вертикальная сила транспортного средства вдоль зафиксированной шиной оси z | N |
| Опрокидывание момента о зафиксированной шиной оси X | N· |
| Крутящий момент сопротивления качению о зафиксированной шиной оси Y | N· |
Mz | Выравнивание момента о зафиксированной шиной оси z | N· |
| Транспортное средство продольная скорость вдоль зафиксированной шиной оси X | m/s |
| Поперечная скорость транспортного средства вдоль зафиксированной шиной оси Y | m/s |
| Загруженный эффективный радиус | m |
| Продольное отношение промаха | N/A |
| Угол заноса | рад |
| Свяжитесь с закрашенной фигурой половина длины | m |
| Свяжитесь с полушириной закрашенной фигуры | m |
| Угол изгиба | рад |
| Утомите скорость вращения о зафиксированной шиной оси z (уровень рыскания) | рад/с |
| Ось вертикальное смещение вдоль зафиксированной шиной оси z | m |
| Вертикальная сила боковой стены на земле вдоль зафиксированной шиной оси z | N |
| Давление накачивания шин | Па |
Fx — Продольная сила осиscalar | N- 1 векторПродольная сила, действующая на ось, Fx, вдоль зафиксированной шиной оси X, в N. Положительная сила действует, чтобы переместить транспортное средство вперед.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fy — Боковая сила осиscalar | N- 1 векторБоковая сила, действующая на ось, Fy, вдоль зафиксированной шиной оси Y, в N.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fz — Вертикальная сила осиscalar | N- 1 векторВертикальная сила, действующая на ось, Fz, вдоль зафиксированной шиной оси z, в N.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Mx — Опрокидывание моментаscalar | N- 1 векторПродольный момент, действуя на ось, Mx, о зафиксированной шиной оси X, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
My — Прокрутка резистивного моментаscalar | N- 1 векторБоковой момент, действуя на ось, My, о зафиксированной шиной оси Y, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Mz — Выравнивание моментаscalar | N- 1 векторВертикальный момент, действуя на ось, Mz, о зафиксированной шиной оси z, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Tire type ВводExternal file (значение по умолчанию) | Light passenger car 205/60R15 | Mid-size passenger car 235/45R18 | Performance car 225/40R19 | SUV 265/50R20 | Light truck 275/65R18 | Commercial truck 295/75R22.5Используйте параметр Tire type, чтобы выбрать источник данных о шине.
| Цель | Действие |
|---|---|
Реализуйте Волшебную Формулу с помощью эмпирических уравнений1, 2. Подходящие коэффициенты использования уравнений, которые соответствуют параметрам блоков. | Обновите параметры блоков с подходящими коэффициентами из файла:
|
Реализуйте адаптированные наборы данных шины, обеспеченные Глобальным Центром Автомобильной Симуляции Эффективности (GCAPS). | Обновите применимые параметры блоков с GCAPS адаптированные данные о шине:
|
Tire file or object, tireParamSet — Утомите файл.mat | .tir | .txtФайл шины .tir или объект, содержащий эмпирические данные к шине модели продольное и боковое поведение с Волшебной Формулой. Если вы обеспечиваете .txt файл, убедитесь, что файл содержит имена, которые соответствуют параметрам блоков.
Обновите параметры блоков с подходящими коэффициентами из файла:
Установите Tire type на External file.
На панели External tire source выберите Select file.
Выберите содействующий файл шины.
Выберите Update mask values from file. В диалоговом окне, которое предлагает вам подтверждение, нажмите OK. Блок обновляет параметры.
Выберите Apply.
Tire side — Выберите сторону шиныRight (значение по умолчанию) | Left | SymmetricЗадайте сторону шины.
Tire pressure — ДавлениеscalarДавление накачивания шин, p, в Па.
Чтобы включить этот параметр, очистите Input tire pressure.
Maximum pressure, PRESMAX — ДавлениеscalarМаксимальное давление, PRESMAX, в Па.
Minimum pressure, PRESMIN — ДавлениеscalarМинимальное давление, PRESMIN, в Па.
Maximum normal force, FZMAX СилаscalarМаксимальная нормальная сила, FZMAX, в N.
Minimum normal force, FZMIN СилаscalarМинимальная нормальная сила, FZMIN, в N.
Velocity tolerance used to handle low velocity situations, VXLOW ДопускscalarСкоростной допуск раньше обрабатывал ситуации низкой скорости, VXLOW, в m/s.
Max allowable slip ratio (absolute), KPUMAX — ОтношениеscalarMax допустимое (абсолютное) отношение промаха, KPUMAX, безразмерный.
Minimum allowable slip ratio (absolute), KPUMIN — ОтношениеscalarМинимальное допустимое (абсолютное) отношение промаха, KPUMIN, безразмерный.
Max allowable slip angle (absolute), ALPMAX \anglescalarMax допустимый (абсолютный) угол промаха, ALPMAX, в рад.
Minimum allowable slip angle (absolute), ALPMIN \anglescalarМинимальный допустимый (абсолютный) угол промаха, ALPMIN, в рад.
Maximum allowable camber angle, CAMMAX \anglescalarМаксимальный допустимый угол изгиба CAMMAX, в рад.
Minimum allowable camber angle, CAMMIN \anglescalarМинимальный допустимый угол изгиба, CAMMIN, в рад.
Nominal longitudinal speed, LONGVL — СкоростьscalarНоминальная продольная скорость, LONGVL, в m/s.
Default tyre side, tyreside — Сторона'Right' (значение по умолчанию) | charСторона шины по умолчанию, tyreside, безразмерный.
Initial rotational velocity, omegao — СкоростьscalarНачальная вращательная скорость, omegao, в rad/s.
Rotational damping, br — ЗатуханиеscalarВращательное затухание, br, в N · m·.
Unloaded radius, UNLOADED_RADIUS — РадиусscalarРазгруженный радиус, UNLOADED_RADIUS, в m.
Nominal pressure, NOMPRES — ДавлениеscalarНоминальное давление, NOMPRES, в Па.
Nominal normal force, FNOMIN СилаscalarНоминальная нормальная сила, FNOMIN, в N.
Wheel width, WIDTH widthscalarШирина колеса, WIDTH, в m.
Rim radius, RIM_RADIUS — РадиусscalarРадиус оправы, RIM_RADIUS, в m.
Nominal aspect ratio, ASPECT_RATIO — ОтношениеscalarНоминальное соотношение сторон, ASPECT_RATIO, безразмерный.
Wheel mass, MASS — МассаscalarМасса колеса, MASS, в kg.
Rotational inertia (rolling axis), IYY — ИнерцияscalarВращательная инерция (прокручивающий ось), IYY, в kg · м^2.
Gravity, GRAVITY — Сила тяжестиscalarСила тяжести, GRAVITY, в м/с^2.
Initial tire displacement, zo — СмещениеscalarНачальное смещение шины, zo, в m.
Initial wheel vertical velocity (wheel fixed frame), zdoto — СкоростьscalarНачальное колесо вертикальная скорость (колесо зафиксированная система координат), zdoto, в m/s.
Effective rolling radius at low load stiffness, BREFF — ЖесткостьscalarЭффективный радиус прокрутки в низкой жесткости загрузки, BREFF, безразмерном.
Effective rolling radius peak value, DREFF — РадиусscalarЭффективное пиковое значение радиуса прокрутки, DREFF, безразмерный.
Effective rolling radius at high load stiffness, FREFF — РадиусscalarЭффективный радиус прокрутки в высокой жесткости загрузки, FREFF, безразмерном.
Unloaded to nominal rolling radius ratio, Q_RE0 — ОтношениеscalarРазгруженный к номинальному отношению радиуса прокрутки, Q_RE0, безразмерному.
Radius rotational speed dependence, Q_V1 — СкоростьscalarЗависимость скорости вращения радиуса, Q_V1, безразмерный.
Stiffness rotational speed dependence, Q_V2 — СкоростьscalarЗависимость скорости вращения жесткости, Q_V2, безразмерный.
Linear load change with deflection, Q_FZ1 — Загрузите изменениеscalarЛинейное изменение загрузки с отклонением, Q_FZ1, безразмерным.
Quadratic load change with deflection, Q_FZ2 — Загрузите изменениеscalarКвадратичное изменение загрузки с отклонением, Q_FZ2, безразмерным.
Linear load change with deflection and quadratic camber, Q_FZ3 — Загрузите изменениеscalarЛинейное изменение загрузки с отклонением и квадратичным изгибом, Q_FZ3, безразмерным.
Load response to longitudinal force, Q_FCX СилаscalarЗагрузите ответ на продольную силу, Q_FCX, безразмерный.
Load response to lateral force, Q_FCY СилаscalarЗагрузите ответ на боковую силу, Q_FCY, безразмерный.
Vertical stiffness change due to lateral load dependency on lateral stiffness, Q_FCY2 — ЖесткостьscalarВертикальное изменение жесткости из-за боковой зависимости от загрузки от боковой жесткости, Q_FCY2, безразмерного.
Stiffness response to pressure, PFZ1 — ЖесткостьscalarОтвет жесткости на давление, PFZ1, безразмерный.
Vertical tire stiffness, VERTICAL_STIFFNESS — ЖесткостьscalarВертикальная жесткость шины, VERTICAL_STIFFNESS, в N/m.
Vertical tire damping, VERTICAL_DAMPING — ЗатуханиеscalarВертикальное затухание шины, VERTICAL_DAMPING, в N · s/m.
Rim bottoming out offset, BOTTOM_OFFST — СмещениеscalarОправа, достигающая нижнего предела смещение, BOTTOM_OFFST, в m.
Bottoming out stiffness, BOTTOM_STIFF — ЖесткостьscalarДостигая нижнего предела жесткость, BOTTOM_STIFF, в N/m.
Linear load dependent camber angle influence on vertical stiffness, Q_CAM1 — ЖесткостьscalarЛинейный зависимый угол изгиба загрузки влияет на вертикальной жесткости, Q_CAM1, безразмерном.
Quadratic load dependent camber angle influence on vertical stiffness, Q_CAM2 — ЖесткостьscalarКвадратичный зависимый угол изгиба загрузки влияет на вертикальной жесткости, Q_CAM2, безразмерном.
Linear load and camber angle dependent reduction on vertical stiffness, Q_CAM3 — ЖесткостьscalarЛинейная загрузка и угловое зависимое сокращение изгиба на вертикальной жесткости, Q_CAM3, безразмерном.
Longitudinal stiffness, LONGITUDINAL_STIFFNESS — ЖесткостьscalarПродольная жесткость, LONGITUDINAL_STIFFNESS, в N/m.
Lateral stiffness, LATERAL_STIFFNESS — ЖесткостьscalarПродольная жесткость, LATERAL_STIFFNESS, в N/m.
Linear vertical deflection influence on longitudinal stiffness, PCFX1 — Влияние отклоненияscalarЛинейное вертикальное отклонение влияет на продольной жесткости, PCFX1, безразмерном.
Quadratic vertical deflection influence on longitudinal stiffness, PCFX2 — Влияние отклоненияscalarКвадратичное вертикальное отклонение влияет на продольной жесткости, PCFX2, безразмерном.
Pressure dependency on longitudinal stiffness, PCFX3 — Зависимость от давленияscalarЗависимость от давления от продольной жесткости, PCFX3, безразмерного.
Linear vertical deflection influence on lateral stiffness, PCFY1 — Влияние отклоненияscalarЛинейное вертикальное отклонение влияет на боковой жесткости, PCFY1, безразмерном.
Quadratic vertical deflection influence on lateral stiffness, PCFY2 — Влияние отклоненияscalarКвадратичное вертикальное отклонение влияет на боковой жесткости, PCFY2, безразмерном.
Pressure dependency on longitudinal stiffness, PCFY3 — Зависимость от давленияscalarЗависимость от давления от продольной жесткости, PCFY3, безразмерного.
Contact length square root term, Q_RA1 — Термин длиныscalarСвяжитесь с термином квадратного корня длины, Q_RA1, безразмерным.
Contact length linear term, Q_RA2 — Термин длиныscalarСвяжитесь с линейным членом длины, Q_RA2, безразмерным.
Contact width root term, Q_RB1 — Термин шириныscalarСвяжитесь с корневым термином ширины, Q_RB1, безразмерным.
Contact width linear term, Q_RB2 — Термин шириныscalarСвяжитесь с линейным членом ширины, Q_RB2, безразмерным.
Cfx shape factor, PCX1 — Масштабный факторscalarМасштабный фактор, Cfx, PCX1, безразмерный.
Longitudinal friction at nominal normal load, PDX1 — ТрениеscalarПродольное трение при номинальной нормальной загрузке, PDX1, безразмерном.
Frictional variation with load, PDX2 — Изменение тренияscalarФрикционное изменение с загрузкой, PDX2, безразмерным.
Frictional variation with camber, PDX3 — Изменение тренияscalarФрикционное изменение с изгибом, PDX3, в 1/rad^2.
Longitudinal curvature at nominal normal load, PEX1 — ИскривлениеscalarПродольное искривление при номинальной нормальной загрузке, PEX1, безразмерном.
Variation of curvature factor with load, PEX2 — Изменение искривленияscalarИзменение фактора искривления с загрузкой, PEX2, безразмерным.
Variation of curvature factor with square of load, PEX3 — Изменение искривленияscalarИзменение фактора искривления с квадратом загрузки, PEX3, безразмерного.
Longitudinal curvature factor with slip, PEX4 — ИскривлениеscalarПродольный фактор искривления с промахом, PEX4, безразмерным.
Longitudinal slip stiffness at nominal normal load, PKX1 — ЖесткостьscalarПродольная жесткость промаха при номинальной нормальной загрузке, PKX1, безразмерном.
Variation of slip stiffness with load, PKX2 — Изменение жесткостиscalarИзменение жесткости промаха с загрузкой, PKX2, безразмерным.
Slip stiffness exponent factor, PKX3 — Подсуньте жесткостьscalarПодсуньте фактор экспоненты жесткости, PKX3, безразмерный.
Horizontal shift in slip ratio at nominal normal load, PHX1 — Подсуньте сдвиг отношенияscalarГоризонталь переключает отношение промаха на нижний регистр при номинальной нормальной загрузке, PHX1, безразмерном.
Variation of horizontal slip ratio with load, PHX2 — Подсуньте изменениеscalarИзменение горизонтального отношения промаха с загрузкой, PHX2, безразмерным.
Vertical shift in load at nominal normal load, PVX1 — Загрузите сдвигscalarВертикальный сдвиг в загрузке при номинальной нормальной загрузке, PVX1, безразмерном.
Variation of vertical shift with load, PVX2 — Загрузите изменениеscalarИзменение вертикального сдвига с загрузкой, PVX2, безразмерным.
Linear variation of longitudinal slip stiffness with tire pressure, PPX1 — Изменение жесткостиscalarЛинейное изменение продольной жесткости промаха с давлением воздуха в шине, PPX1, безразмерным.
Quadratic variation of longitudinal slip stiffness with tire pressure, PPX2 — Изменение жесткостиscalarКвадратичное изменение продольной жесткости промаха с давлением воздуха в шине, PPX2, безразмерным.
Linear variation of peak longitudinal friction with tire pressure, PPX3 — Изменение тренияscalarЛинейное изменение пикового продольного трения с давлением воздуха в шине, PPX3, безразмерным.
Quadratic variation of peak longitudinal friction with tire pressure, PPX4 — Изменение тренияscalarКвадратичное изменение пикового продольного трения с давлением воздуха в шине, PPX4, безразмерным.
Combined slip Fx slope factor reduction, RBX1 — Объединенный промах продольная сила клонится факторное сокращениеscalarОбъединенный промах продольная сила, Fx, клонится факторное сокращение, RBX1, безразмерный.
Slip ratio Fx slope reduction variation, RBX2 — Подсуньте отношению продольное изменение сокращения наклона силыscalarПодсуньте отношению продольную силу, Fx, наклонное изменение сокращения, RBX2, безразмерный.
Camber influence on combined slip Fx stiffness, RBX3 — Влияние изгиба на объединенный промах продольная жесткость силыscalarВлияние изгиба на объединенный промах продольная сила, Fx, жесткость, RBX3, безразмерный.
Shape factor for combined slip Fx reduction, RCX1 — Масштабный фактор для объединенного промаха продольное сокращение силыscalarМасштабный фактор для объединенного промаха продольная сила, Fx, сокращение, RCX1, безразмерный.
Combined Fx curvature factor, REX1 — Объединенный продольный фактор искривления силыscalarОбъединенная продольная сила, Fx, фактор искривления, REX1, безразмерный.
Combined Fx curvature factor with load, REX2 — Объединенный продольный фактор искривления силыscalarОбъединенная продольная сила, Fx, фактор искривления с загрузкой, REX2, безразмерным.
Combined slip Fx shift factor reduction, RHX1 — Объединенный промах продольный фактор промаха силыscalarОбъединенный промах продольная сила, Fx, сокращение коэффициента сдвига, RHX1, безразмерный.
Vertical shift of overturning moment, QSX1 — Опрокидывание моментаscalarВертикальный сдвиг опрокидывающегося момента, QSX1, безразмерного.
Overturning moment due to camber, QSX2 — Опрокидывание момента из-за изгибаscalarОпрокидывая момент из-за изгиба, QSX2, безразмерного.
Overturning moment due to Fy, QSX3 — Опрокидывание момента из-за боковой силыscalarОпрокидывая момент из-за боковой силы, QSX3, безразмерного.
Mx combined lateral force load and camber, QSX4 — Опрокидывание моментаscalarОпрокидывание момента, Mx, объединило боковую загрузку силы и изгиб, QSX4, безразмерный.
Mx load effect due to lateral force and camber, QSX5 — Опрокидывание моментаscalarОпрокидывание момента, Mx, загружает эффект из-за боковой силы и изгиба, QSX5, безразмерного.
Mx load effect due to B-factor, QSX6 — Опрокидывание моментаscalarОпрокидывание момента, Mx, загружает эффект из-за B-фактора, QSX6, безразмерного.
Mx due to camber and load, QSX7 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за изгиба и загрузки, QSX7, безразмерного.
Mx due to lateral force and load, QSX8 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за боковой силы и загрузки, QSX8, безразмерного.
Mx due to B-factor of lateral force and load, QSX9 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за B-фактора боковой силы и загрузки, QSX9, безразмерного.
Mx due to vertical force and camber, QSX10 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за вертикальной силы и изгиба, QSX10, безразмерного.
Mx due to B-factor of vertical force and camber, QSX11 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за B-фактора вертикальной силы и изгиба, QSX11, безразмерного.
Mx due to squared camber, QSX12 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за изгиба в квадрате, QSX12, безразмерного.
Mx due to lateral force, QSX13 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за боковой силы, QSX13, безразмерного.
Mx due to lateral force with camber, QSX14 — Опрокидывание моментаscalarОпрокидывая момент, Mx, из-за боковой силы с изгибом, QSX14, безразмерным.
Mx due to inflation pressure, PPMX1 — Опрокидывание момента из-за давленияscalarОпрокидывая момент, Mx, из-за давления инфляции, PPMX1, безразмерного.
Cfy shape factor for lateral force, PCY1 — Боковой масштабный фактор силыscalarМасштабный фактор для боковой силы, Cfy, PCY1, безразмерного.
Lateral friction muy, PDY1 — Боковое трениеscalarБоковое трение, μy, PDY1, безразмерный.
Lateral friction variation of muy with load, PDY2 — Боковое изменение тренияscalarИзменение бокового трения, μy, с загрузкой, PDY2, безразмерным.
Lateral friction variation of muy with squared camber, PDY3 — Боковое изменение тренияscalarИзменение бокового трения, μy, с изгибом в квадрате, PDY3, безразмерным.
Efy lateral curvature at nominal force FZNOM, PEY1 — Боковое искривление в номинальной силеscalarБоковое искривление, Efy, в номинальной силе, FZNOM, PEY1, безразмерном.
Efy curvature variation with load, PEY2 — Боковое изменение искривленияscalarБоковое искривление, Efy, изменение с загрузкой, PEY2, безразмерным.
Efy curvature constant camber dependency, PEY3 — Боковое постоянное искривлениеscalarБоковое искривление, Efy, постоянная зависимость от изгиба, PEY3, безразмерный.
Efy curvature variation with camber, PEY4 — Боковое изменение искривленияscalarБоковое искривление, Efy, изменение с изгибом, PEY4, безразмерным.
Efy curvature variation with camber squared, PEY5 — Боковое изменение искривленияscalarБоковое искривление, Efy, изменение с изгибом придало квадратную форму, PEY5, безразмерный.
Maximum KFy/FZNOM stiffness, PKY1 — Максимальная жесткостьscalarМаксимальное ответвление обеспечивает жесткость, KFy, к номинальной силе, FZNOM, отношению, PKY1, безразмерному.
Load at maximum KFy/FZNOM stiffness, PKY2 загрузкаscalarЗагрузите в максимальной боковой жесткости силы, KFy, к номинальной силе, FZNOM, отношению, PKY2, безразмерному.
KFy/FZNOM stiffness variation with camber, PKY3 — Изменение жесткостиscalarБоковая жесткость силы, KFy, к номинальной силе, FZNOM, изменению жесткости с изгибом, PKY3, безразмерным.
KFy curvature, PKY4 — Боковое искривление жесткости силыscalarБоковая жесткость силы, искривление KFy, PKY4, безразмерный.
Variation of peak stiffness with squared camber, PKY5 — Изменение жесткостиscalarИзменение пиковой жесткости с изгибом в квадрате, PKY5, безразмерным.
Fy camber stiffness factor, PKY6 — Боковой фактор жесткости изгиба силыscalarБоковая сила, Fy, фактор жесткости изгиба, PKY6, безразмерный.
Camber stiffness vertical load dependency, PKY7 — ЖесткостьscalarЖесткость изгиба вертикальная зависимость от загрузки, PKY7, безразмерный.
SHY horizontal shift at FZNOM, PHY1 — Горизонтальный сдвиг в номинальной силеscalarГоризонтальный сдвиг, SHY, в номинальной силе, FZNOM, PHY1, безразмерном.
SHY variation with load, PHY2 — Горизонтальное изменение сдвигаscalarГоризонтальный сдвиг, SHY, изменение с загрузкой, PHY2, безразмерным.
Svy/Fz vertical shift at FZNOM, PVY1 — Вертикальный сдвиг в номинальной силеscalarВертикальный сдвиг, Svy, в номинальной силе, FZNOM, PVY1, безразмерном.
Svy/Fz variation with load, PVY2 — Вертикальное изменение сдвига с загрузкойscalarВертикальный сдвиг, Svy, изменение с загрузкой, PVY2, безразмерным.
Svy/Fz variation with camber, PVY3 — Вертикальное изменение сдвига с изгибомscalarВертикальный сдвиг, Svy, изменение с изгибом, PVY3, безразмерным.
Svy/Fz variation with load and camber, PVY4 — Вертикальное изменение сдвига с загрузкой и изгибомscalarВертикальный сдвиг, Svy, изменение с загрузкой и изгибом, PVY4, безразмерным.
Cornering stiffness variation with inflation pressure, PPY1 — Изменение жесткости с давлениемscalarЗагоняя изменение жесткости в угол с давлением инфляции, PPY1, безразмерным.
Cornering stiffness variation with inflation pressure induced nominal load dependency, PPY2 — Изменение жесткости с давлениемscalarДвижение на повороте изменения жесткости с давлением инфляции вызвало номинальную зависимость от загрузки, PPY2, безразмерный.
Linear inflation pressure on peak lateral friction, PPY3 — ДавлениеscalarЛинейное давление инфляции на пиковое боковое трение, PPY3, безразмерный.
Quadratic inflation pressure on peak lateral friction, PPY4 — ДавлениеscalarКвадратичное давление инфляции на пиковое боковое трение, PPY4, безразмерный.
Inflation pressure effect on camber stiffness, PPY5 — ДавлениеscalarВоздействие давления инфляции на жесткости изгиба, PPY5, безразмерном.
Combined Fy reduction slope factor, RBY1 — Объединенное боковое сокращение силы клонится факторscalarОбъединенная боковая сила, Fy, сокращение клонится фактор, RBY1, безразмерный.
Fy slope reduction with slip angle, RBY2 — Боковое сокращение наклона силы с углом промахаscalarБоковая сила, Fy, наклонное сокращение с углом промаха, RBY2, безразмерным.
Fy shift reduction with slip angle, RBY3 — Боковое сокращение сдвига силы с углом промахаscalarБоковая сила, Fy, переключает сокращение с углом промаха, RBY3, безразмерным.
Fy combined stiffness variation from camber, RBY4 — Боковая сила объединила изменение жесткости от изгибаscalarБоковая сила, Fy, объединила изменение жесткости от изгиба, RBY4, безразмерного.
Fy combined reduction shape factor, RCY1 — Боковая сила объединила масштабный фактор сокращенияscalarБоковая сила, Fy, объединила масштабный фактор сокращения, RCY1, безразмерный.
Fy combined curvature factor, REY1 — Боковая сила объединила фактор искривленияscalarБоковая сила, Fy, объединила фактор искривления, REY1, безразмерный.
Fy combined curvature factor with load, REY2 — Боковая сила объединила фактор искривления с загрузкойscalarБоковая сила, Fy, объединила фактор искривления с загрузкой, REY2, безразмерным.
Fy combined reduction shift factor, RHY1 — Боковая сила объединила коэффициент сдвига сокращенияscalarБоковая сила, Fy, объединила коэффициент сдвига сокращения, RHY1, безразмерный.
Fy combined reduction shift factor with load, RHY2 — Боковая сила объединила коэффициент сдвига сокращения с загрузкойscalarБоковая сила, Fy, объединила коэффициент сдвига сокращения с загрузкой, RHY2, безразмерным.
Slip ratio side force Svyk/Muy*Fz at FZNOM, RVY1 — Подсуньте силу понижения отношения в номинальной силеscalarПодсуньте силу стороны отношения в номинальной силе, FZNOM, RVY1, безразмерном.
Side force Svyk/Muy*Fz variation with load, RVY2 — Изменение силы стороны с загрузкойscalarИзменение силы стороны с загрузкой, RVY2, безразмерным.
Side force Svyk/Muy*Fz variation with camber, RVY3 — Изменение силы стороны с изгибомscalarИзменение силы стороны с изгибом, RVY3, безразмерным.
Side force Svyk/Muy*Fz variation with slip angle, RVY4 — Изменение силы стороны с углом промахаscalarИзменение силы стороны с углом промаха, RVY4, безразмерным.
Side force Svyk/Muy*Fz variation with slip ratio, RVY5 — Изменение силы стороны с отношением промахаscalarИзменение силы стороны с отношением промаха, RVY5, безразмерным.
Side force Svyk/Muy*Fz variation with slip ratio arctangent, RVY6 — Изменение силы стороны с арктангенсом отношения промахаscalarИзменение силы стороны с арктангенсом отношения промаха, RVY6, безразмерным.
Torque resistance coefficient, QSY1 — Закрутите сопротивлениеscalarЗакрутите коэффициент сопротивления, QSY1, безразмерный.
Torque resistance due to Fx, QSY2 — Закрутите сопротивление из-за продольной силыscalarЗакрутите сопротивление из-за продольной силы, Fx, QSY2, безразмерного.
Torque resistance due to speed, QSY3 — Закрутите сопротивление из-за скоростиscalarЗакрутите сопротивление из-за скорости, QSY3, безразмерного.
Torque resistance due to speed^4, QSY4 — Закрутите сопротивление из-за скоростиscalarЗакрутите сопротивление из-за speed^4, QSY4, безразмерного.
Torque resistance due to square of camber, QSY5 — Закрутите сопротивление из-за изгибаscalarЗакрутите сопротивление из-за квадрата изгиба, QSY5, безразмерного.
Torque resistance due to square of camber and load, QSY6 — Закрутите сопротивление из-за изгиба и загрузкиscalarЗакрутите сопротивление из-за квадрата изгиба и загрузки, QSY6, безразмерного.
Torque resistance due to load, QSY7 — Закрутите сопротивление, должное загружатьscalarЗакрутите сопротивление, должное загружать, QSY7, безразмерный.
Torque resistance due to pressure, QSY8 — Закрутите сопротивление из-за давленияscalarЗакрутите сопротивление из-за давления, QSY8, безразмерного.
Trail slope factor for trail Bpt at FZNOM, QBZ1 — Фактор наклона следа в номинальной силеscalarФактор наклона следа для следа Bpt в номинальной силе, FZNOM, QBZ1, безразмерном.
Bpt slope variation with load, QBZ2 — Наклонное изменение с загрузкойscalarНаклонное изменение с загрузкой, QBZ2, безразмерным.
Bpt slope variation with square of load, QBZ3 — Наклонное изменение с загрузкойscalarНаклонное изменение с квадратом загрузки, QBZ3, безразмерного.
Bpt slope variation with camber, QBZ4 — Наклонное изменение с изгибомscalarНаклонное изменение с изгибом, QBZ4, безразмерным.
Bpt slope variation with absolute value of camber, QBZ5 — Наклонное изменение с изгибомscalarНаклонное изменение с абсолютным значением изгиба, QBZ5, безразмерного.
Bpt slope variation with square of camber, QBZ6 — Наклонное изменение с изгибомscalarНаклонное изменение с квадратом изгиба, QBZ6, безразмерного.
Br of Mzr slope scaling factor, QBZ9 — Наклонный масштабный коэффициентscalarНаклонный масштабный коэффициент, QBZ9, безразмерный.
Br of Mzr cornering stiffness factor, QBZ10 — Движение на повороте фактора жесткостиscalarBr Mzr, загоняющего в угол фактор жесткости, QBZ10, безразмерный.
Cpt pneumatic trail shape factor, QCZ1 — Пневматический масштабный фактор следаscalarПневматический масштабный фактор следа, Cpt, QCZ1, безразмерный.
Dpt peak trail, QDZ1 — Пиковый следscalarПиковый след, Dpt, QDZ1, безразмерный.
Dpt peak trail variation with load, QDZ2 — Пиковое изменение следа с загрузкойscalarПиковый след, Dpt, изменение с загрузкой, QDZ2, безразмерным.
Dpt peak trail variation with camber, QDZ3 — Пиковое изменение следа с изгибомscalarПиковый след, Dpt, изменение с изгибом, QDZ3, безразмерным.
Dpt peak trail variation with square of camber, QDZ4 — Пиковое изменение следа с изгибомscalarПиковый след, Dpt, изменение с квадратом изгиба, QDZ4, безразмерного.
Dmr peak residual torque, QDZ6 — Пиковый остаточный крутящий моментscalarПиковый остаточный крутящий момент, Dmr, QDZ6, безразмерный.
Dmr peak residual torque variation with load, QDZ7 — Пиковая невязка закручивает изменение с загрузкойscalarПиковый остаточный крутящий момент, Dmr, изменение с загрузкой, QDZ7, безразмерным.
Dmr peak residual torque variation with camber, QDZ8 — Пиковая невязка закручивает изменение с изгибомscalarПиковый остаточный крутящий момент, Dmr, изменение с изгибом, QDZ8, безразмерным.
Dmr peak residual torque variation with camber and load, QDZ9 — Пиковая невязка закручивает изменение с изгибом и загрузкуscalarПиковый остаточный крутящий момент, Dmr, изменение с изгибом и загрузка, QDZ9, безразмерный.
Dmr peak residual torque variation with square of camber, QDZ10 — Пиковая невязка закручивает изменение с изгибомscalarПиковый остаточный крутящий момент, Dmr, изменение с квадратом изгиба, QDZ10, безразмерного.
Dmr peak residual torque variation with square of load, QDZ11 — Пиковая невязка закручивает изменение с загрузкойscalarПиковый остаточный крутящий момент, Dmr, изменение с квадратом загрузки, QDZ11, безразмерного.
Ept trail curvature at FZNOM, QEZ1 — Искривление следа в номинальной силеscalarИскривление следа, Ept, в номинальной силе, FZNOM, QEZ1, безразмерном.
Ept variation with load, QEZ2 — Изменение искривления следа с загрузкойscalarИскривление следа, изменение Ept с загрузкой, QEZ2, безразмерным.
Ept variation with square of load, QEZ3 — Изменение искривления следа с загрузкойscalarИскривление следа, изменение Ept с квадратом загрузки, QEZ3, безразмерного.
Ept variation with sign of alpha-t, QEZ4 — Изменение искривления следаscalarИскривление следа, изменение Ept со знаком альфы-t, QEZ4, безразмерного.
Ept variation with sign of alpha-t and camber, QEZ5 — ИзменениеscalarИскривление следа, изменение Ept со знаком альфы-t и изгиба, QEZ5, безразмерного.
Sht horizontal trail shift at FZNOM, QHZ1 — Горизонтальный сдвиг следа при номинальной загрузкеscalarГоризонтальный сдвиг следа, Sht, при номинальной загрузке, FZNOM, QHZ1, безразмерном.
Sht variation with load, QHZ2 — Горизонтальное изменение сдвига следа с загрузкойscalarГоризонтальный сдвиг следа, Sht, изменение с загрузкой, QHZ2, безразмерным.
Sht variation with camber, QHZ3 — Горизонтальное изменение сдвига следа с изгибомscalarГоризонтальный сдвиг следа, Sht, изменение с изгибом, QHZ3, безразмерным.
Sht variation with load and camber, QHZ4 — Горизонтальное изменение сдвига следа с загрузкой и изгибомscalarГоризонтальный сдвиг следа, Sht, изменение с загрузкой и изгибом, QHZ4, безразмерным.
Inflation pressure influence on trail length, PPZ1 — Влияние давления на длину следаscalarДавление инфляции влияет на длине следа, PPZ1, безразмерном.
Inflation pressure influence on residual aligning torque, PPZ2 — Влияние давления на выравнивающийся крутящий моментscalarДавление инфляции влияет на крутящем моменте выравнивания невязки, PPZ2, безразмерном.
Nominal value of s/R0: effect of Fx on Mz, SSZ1 — Эффект продольной силы на выравнивающемся крутящем моментеscalarНоминальная стоимость s/R0: эффект продольной силы, Fx, на выравнивающемся крутящем моменте, Mz, SSZ1, безразмерном.
s/R0 variation with lateral to nominal force ratio, SSZ2 — Изменение с ответвлением к номинальному отношению силыscalarИзменение с ответвлением к номинальному отношению силы, SSZ2, безразмерному.
s/R0 variation with camber, SSZ3 — Изменение с изгибомscalarИзменение с изгибом, SSZ3, безразмерным.
s/R0 variation with camber and load, SSZ4 — Изменение с изгибом и загрузкаscalarИзменение с изгибом и загрузка, SSZ4, безразмерный.
Fx peak reduction due to spin, PDXP1 — Продольное сокращение пика силы, должное вращатьсяscalarПродольная сила, Fx, пиковое сокращение, должное вращаться, PDXP1, безразмерный.
Fx peak reduction due to spin with varying load, PDXP2 — Продольное сокращение пика силы, должное вращатьсяscalarПродольная сила, Fx, пиковое сокращение, должное вращаться с различной загрузкой, PDXP2, безразмерным.
Fx peak reduction due to spin with slip ratio, PDXP3 — Продольное сокращение пика силы, должное вращатьсяscalarПродольная сила, Fx, пиковое сокращение, должное вращаться с отношением промаха, PDXP3, безразмерным.
Cornering stiffness reduction due to spin, PKYP1 — Сокращение жесткости, должное вращатьсяscalarЗагоняя в угол сокращение жесткости, должное вращаться, PKYP1, безразмерный.
Fy peak reduction due to spin, PDYP1 — Боковое сокращение пика силы, должное вращатьсяscalarБоковая сила, Fy, пиковое сокращение, должное вращаться, PDYP1, безразмерный.
Fy peak reduction due to spin with varying load, PDYP2 — Боковое сокращение пика силы, должное вращатьсяscalarБоковая сила, Fy, пиковое сокращение, должное вращаться с различной загрузкой, PDYP2, безразмерным.
Fy peak reduction due to spin with slip angle, PDYP3 — Боковое сокращение пика силы, должное вращатьсяscalarБоковая сила, Fy, пиковое сокращение, должное вращаться с углом промаха, PDYP3, безразмерным.
Fy peak reduction due to square root of spin, PDYP4 — Боковое сокращение пика силы, должное вращатьсяscalarБоковая сила, Fy, пиковое сокращение из-за квадратного корня из вращения, PDYP4, безразмерного.
Fy vs. slip angle response lateral shift limit, PHYP1 — Боковая сила по сравнению с угловым ответом промахаscalarБоковая сила, Fy, по сравнению с угловым ответвлением ответа промаха переключают предел, PHYP1, безразмерный.
Fy vs. slip angle response max lateral shift limit, PHYP2 — Боковая сила по сравнению с угловым ответом промахаscalarБоковая сила, Fy, по сравнению с угловым ответом промаха макс. боковой предел сдвига, PHYP2, безразмерный.
Fy vs. slip angle response max lateral shift limit with load, PHYP3 — Боковая сила по сравнению с угловым ответом промахаscalarБоковая сила, Fy, по сравнению с угловым ответом промаха макс. боковой предел сдвига с загрузкой, PHYP3, безразмерным.
Fy vs. slip angle response lateral shift curvature factor, PHYP4 — Боковая сила по сравнению с угловым ответом промахаscalarБоковая сила, Fy, по сравнению с угловым ответвлением ответа промаха переключают фактор искривления, PHYP4, безразмерный.
Camber stiffness reduction due to spin, PECP1 — Сокращение жесткости изгибаscalarСокращение жесткости изгиба, должное вращаться, PECP1, безразмерный.
Camber stiffness reduction due to spin with load, PECP2 — Сокращение жесткости изгибаscalarСокращение жесткости изгиба, должное вращаться с загрузкой, PECP2, безразмерным.
Turn slip pneumatic trail reduction factor, QDTP1 — Поверните промах пневматический фактор сокращения следаscalarПоверните промах пневматический фактор сокращения следа, QDTP1, безразмерный.
Turn moment for constant turning and zero longitudinal speed, QCRP1 — Поверните момент для постоянного превращенияscalarПоверните момент для постоянного превращения и обнулите продольную скорость, QCRP1, безразмерный.
Turn slip moment increase with spin at 90deg slip angle, QCRP2 — Поверните момент промахаscalarПоверните увеличение момента промаха с вращением под углом промаха на 90 градусов, QCRP2, безразмерным.
Residual spin torque reduction from side slip, QBRP1 — Остаточное сокращение крутящего момента вращенияscalarОстаточное сокращение крутящего момента вращения от заноса, QBRP1, безразмерного.
Turn slip moment peak magnitude, QDRP1 — Поверните величину пика момента промахаscalarПоверните величину пика момента промаха, QDRP1, безразмерный.
Turn slip moment curvature, QDRP2 — Поверните искривление момента промахаscalarПоверните искривление момента промаха, QDRP2, безразмерный.
[1] Besselink, Igo, Антуан Ж. М. Шмайц и Ханс Б. Пэседжка, "Улучшенная Волшебная модель шины Формулы / Свифта, которая может обработать скачки давления инфляции", Системная Динамика Транспортного средства - Международный журнал Механики Транспортного средства и Мобильности 48, глоток. 1 (2010): 337–52, https://doi.org/10.1080/00423111003748088.
[2] Pacejka, Ханс Б. Тайр и Динамика аппарата. 3-й редактор Оксфорд, Соединенное Королевство: SAE и Баттерворт-Хейнеманн, 2012.
[3] Bohm, F. и Х. П. Виллумейт, "Модели шины для Динамического анализа Транспортного средства: Продолжения 2-го Международного Коллоквиума на Моделях Шины для Анализа Динамики аппарата, Сохраненного в Берлинском техническом университете, Германия, 20-21 февраля 1997". Системная Динамика транспортного средства - Международный журнал Механики Транспортного средства и Мобильности 27, глоток. 1, 343–45. https://doi.org/0.1080/00423119708969669.
[4] Шмид, Стивен Р., Бернард Дж. Хэмрок и Филиал О. Джейкобсон. Основные принципы Элементов Машины, Версии SI. 3-й редактор Бока-Ратон: Нажатие CRC, 2014.
Combined Slip Wheel 2DOF | Combined Slip Wheel 2DOF STI | Fiala Wheel 2DOF | Longitudinal Wheel
[1] Переизданный с разрешением Copyright © 2008 SAE International. Дальнейшее распределение этого материала не разрешено без предшествующего разрешения от SAE.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
