orthfilt
Ортогональные фильтры вейвлета
Синтаксис
Описание
[ вычисляет четыре фильтра, сопоставленные с масштабирующимся фильтром Lo_D,Hi_D,Lo_R,Hi_R] = orthfilt(W)W соответствие вейвлету.
Четыре фильтра, которые вычисляет функция, являются разложением фильтр lowpass Lo_D, разложение highpass фильтрует Hi_D, реконструкция фильтр lowpass Lo_R, и реконструкция highpass фильтрует Hi_R.
Для получения дополнительной информации о том, как функция вычисляет фильтры, см. Алгоритмы.
Примеры
Вычислите ортогональные фильтры вейвлета масштабирующегося фильтра
Создайте масштабирующийся фильтр, сопоставленный с вейвлетом Daubechies, заданным 'db8'.
W = dbwavf('db8'); stem(W); title('Original scaling filter');
Вычислите четыре фильтра, сопоставленные с масштабирующимся фильтром.
[Lo_D,Hi_D,Lo_R,Hi_R] = orthfilt(W);
Постройте разложение фильтр lowpass.
stem(Lo_D);
title('Decomposition lowpass filter'); 
Постройте разложение highpass фильтр.
stem(Hi_D);
title('Decomposition highpass filter'); 
Постройте реконструкцию фильтр lowpass.
stem(Lo_R);
title('Reconstruction lowpass filter'); 
Постройте реконструкцию highpass фильтр.
stem(Hi_R);
title('Reconstruction highpass filter');
Проверяйте на ортонормальность в фильтрах разложения..
df = [Lo_D;Hi_D]; rf = [Lo_R;Hi_R]; id = df*df'
id = 2×2
1.0000 0
0 1.0000
Проверяйте на ортонормальность в фильтрах реконструкции..
id2 = rf*rf'
id2 = 2×2
1.0000 0
0 1.0000
Проверяйте на ортогональность двухместным переводом.
df = [Lo_D 0 0;Hi_D 0 0]; dft = [0 0 Lo_D; 0 0 Hi_D]; zer = df*dft'
zer = 2×2
10-12 ×
-0.1895 -0.0000
0 -0.1895
Постройте низкочастотный модуль передачи.
fftld = fft(Lo_D);
freq = [1:length(Lo_D)]/length(Lo_D);
plot(freq,abs(fftld));
title('Transfer modulus: low-pass'); 
Постройте высокочастотный модуль передачи.
ffthd = fft(Hi_D);
plot(freq,abs(ffthd));
title('Transfer modulus: high-pass')
Входные параметры
Выходные аргументы
Алгоритмы
Для ортогонального вейвлета в среде мультиразрешения начните с масштабирующейся функции ϕ и функции вейвлета ψ. Одно из основных отношений является отношением двойной шкалы:
Все фильтры, используемые в dwt и idwtфункции глубоко связаны с последовательностью . если ϕ сжато поддерживается, последовательность (wn) конечна и может быть просмотрена как КИХ-фильтр. Масштабирующийся фильтр W КИХ-фильтр lowpass длины 2 Н, с суммой 1, и с нормой 1 / √ 2."
Например, для db3 масштабирование фильтра,
w = dbwavf('db3')
w = 0.2352 0.5706 0.3252 -0.0955 -0.0604 0.0249
sum(w)
= 1.000
norm(w)
= 0.7071
Задайте четыре КИХ-фильтра от фильтра W из длины 2 Н и нормы 1.
Функция вычисляет четыре фильтра с помощью следующей схемы.
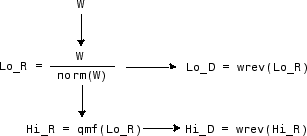
Алгоритм задает qmf таково что Hi_R и Lo_R квадратурные фильтры зеркала (который является Hi_R (k) = (-1)kLo_R(2N + 1 - k), для k = 1, 2, Ä, 2N) и wrev таким образом, что это инвертирует коэффициенты фильтра. Поэтому Hi_D и Lo_D также квадратурные фильтры зеркала.
Ссылки
[1] Daubechies, я. (1992). Десять лекций по вейвлетам. Ряд конференции CBMS-NSF в прикладной математике, SIAM Эд. стр 117–119, 137, 152.