Exponenta Banner

wavedec

1D разложение вейвлета

свернуть все на странице

Синтаксис

[c,l] = wavedec(x,n,wname)
[c,l] = wavedec(x,n,LoD,HiD)

Описание

пример

[c,l] = wavedec(x,n,wname) возвращает разложение вейвлета 1D x сигнала на уровне n использование вейвлета wname. Выходная структура разложения состоит из вектора разложения вейвлета c и бухгалтерский векторный l, который содержит количество коэффициентов уровнем.

Примечание

Для gpuArray входные параметры, поддерживаемыми режимами является 'symh' ('sym') и 'per'. Если входом является gpuArray, дискретный вейвлет преобразовывает дополнительный режим, используемый wavedec значения по умолчанию к 'symh' если текущим дополнительным режимом не является 'per'. Смотрите пример Многоуровневое Дискретное Преобразование Вейвлета на графическом процессоре.

[c,l] = wavedec(x,n,LoD,HiD) возвращает разложение вейвлета с помощью заданного lowpass, и highpass разложение вейвлета фильтрует LoD и HiD, соответственно.

Примеры

свернуть все

Скрипт Open Live Script

Загрузите и постройте одномерный сигнал.

load sumsin 
plot(sumsin)
title('Signal')

Figure contains an axes object. The axes object with title Signal contains an object of type line.

Выполните 3-уровневое разложение вейвлета сигнала с помощью порядка 2 вейвлет Daubechies. Извлеките крупные коэффициенты приближения шкалы и коэффициенты детали от разложения.

[c,l] = wavedec(sumsin,3,'db2');
approx = appcoef(c,l,'db2');
[cd1,cd2,cd3] = detcoef(c,l,[1 2 3]);

Постройте коэффициенты.

subplot(4,1,1)
plot(approx)
title('Approximation Coefficients')
subplot(4,1,2)
plot(cd3)
title('Level 3 Detail Coefficients')
subplot(4,1,3)
plot(cd2)
title('Level 2 Detail Coefficients')
subplot(4,1,4)
plot(cd1)
title('Level 1 Detail Coefficients')

Figure contains 4 axes objects. Axes object 1 with title Approximation Coefficients contains an object of type line. Axes object 2 with title Level 3 Detail Coefficients contains an object of type line. Axes object 3 with title Level 2 Detail Coefficients contains an object of type line. Axes object 4 with title Level 1 Detail Coefficients contains an object of type line.

Этот пример использует:

Скрипт Open Live Script

Пошлите к Поддержке графического процессора Релизом (Parallel Computing Toolbox) видеть то, что поддерживаются графические процессоры.

Загрузите шумный Доплеровский сигнал. Поместите сигнал на графический процессор с помощью gpuArray. Сохраните текущий дополнительный режим.

load noisdopp
noisdoppg = gpuArray(noisdopp);
origMode = dwtmode('status','nodisp');

Используйте dwtmode изменить дополнительный режим в дополнение нуля. Получите трехуровневый DWT сигнала на графическом процессоре с помощью db4 вейвлет.

dwtmode('zpd','nodisp')
[c,l] = wavedec(noisdoppg,3,'db4');

Текущий дополнительный режим zpd не поддерживается для gpuArray входной параметр. Поэтому DWT вместо этого выполняется с помощью sym дополнительный режим. Чтобы подтвердить это, установите дополнительный режим на sym и возьмите DWT noisdoppg, затем сравните с предыдущим результатом.

dwtmode('sym','nodisp')
[csym,lsym] = wavedec(noisdoppg,3,'db4');
[max(abs(c-csym)) max(abs(l-lsym))]
ans =

     0     0

Установите текущий дополнительный режим на per и получите трехуровневый DWT noisdopp. Дополнительный режим per поддерживается для gpuArray входной параметр. Подтвердите, что результат отличается от sym результаты.

dwtmode('per','nodisp')
[cper,lper] = wavedec(noisdoppg,3,'db4');
[length(csym) ; length(cper)]
ans = 2×1

        1044
        1024


[lsym ; lper]
ans = 2×5

         134         134         261         515        1024
         128         128         256         512        1024

Восстановите дополнительный режим к исходной установке.

dwtmode(origMode,'nodisp')

Входные параметры

свернуть все

Входной сигнал в виде вектора.

Типы данных: single | double
Поддержка комплексного числа: Да

Уровень разложения в виде положительного целого числа. wavedec не осуществляет ограничение максимального уровня. Использование wmaxlev гарантировать, что коэффициенты вейвлета свободны от граничных эффектов. Если граничные эффекты не являются беспокойством в вашем приложении, хорошее правило состоит в том, чтобы установить n меньше чем или равный fix(log2(length(x))).

Типы данных: single | double

Анализ вейвлета в виде вектора символов или строкового скаляра.

Примечание

wavedec поддержки только (ортогональный) Тип 1 или Тип 2 (биоортогональные) вейвлеты. Смотрите wfilters для списка ортогональных и биоортогональных вейвлетов.

Разложение вейвлета фильтрует в виде пары ровной длины векторы с действительным знаком. LoD фильтр разложения lowpass и HiD highpass фильтр разложения. Длины LoD и HiD должно быть равным. Смотрите wfilters для получения дополнительной информации.

Типы данных: single | double

Выходные аргументы

свернуть все

Вектор разложения вейвлета, возвращенный как вектор. Бухгалтерский векторный l содержит количество коэффициентов уровнем. Вектор разложения и бухгалтерский вектор организованы как в этой схеме разложения уровня 3.

Типы данных: single | double

Бухгалтерский вектор, возвращенный как вектор из положительных целых чисел. Бухгалтерский вектор используется, чтобы проанализировать коэффициенты в векторе разложения вейвлета c уровнем.

Типы данных: single | double

Алгоритмы

Учитывая s сигнала длины N, DWT состоит из на большинстве шагов log2 N. Начиная с s, первый шаг производит два набора коэффициентов: коэффициенты приближения cA1 и коэффициенты детали cD1. Свертка к s с lowpass фильтрует LoD и highpass фильтруют HiD, сопровождаемый двухместной децимацией (субдискретизация), результаты в приближении и коэффициентах детали соответственно.

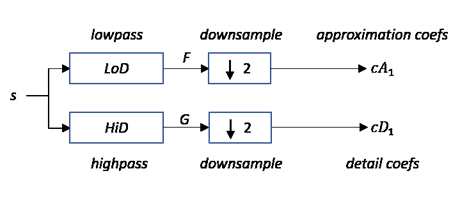
где

  • — Примените операцию свертки с фильтром X

  • ↓2 — Downsample (сохраняют даже индексированные элементы),

Длина каждого фильтра равна 2n. Если N = длина (s), сигналы, F и G имеют длину N + 2n −1 и коэффициенты cA1 и cD1, имеет длину

пол(N−12)+n.

Следующий шаг разделяет коэффициенты приближения cA1 в двух частях с помощью той же схемы, заменяя s cA1, и производя cA2 и cD2, и так далее.

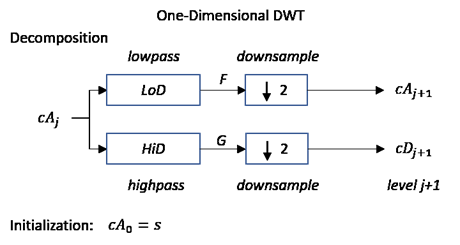
Разложение вейвлета s сигнала, анализируемого на уровне j, имеет следующую структуру: [cAj, cDj..., cD1].

Эта структура содержит, для j = 3, терминальные узлы следующего дерева:

Ссылки

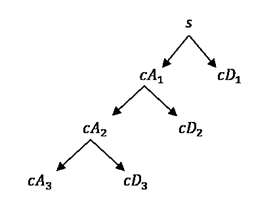
[1] Daubechies, я. Десять лекций по вейвлетам, CBMS-NSF региональный ряд конференции в прикладной математике. Филадельфия, усилитель мощности (УМ): SIAM Эд, 1992.

[2] Mallat, S. G. “Теория для Разложения Сигнала Мультиразрешения: Представление Вейвлета”, Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 11, Выпуск 7, июль 1989, стр 674–693.

[3] Мейер, Y. Вейвлеты и операторы. Переведенный Д. Х. Сэлинджером. Кембридж, Великобритания: Издательство Кембриджского университета, 1995.

Расширенные возможности

Смотрите также

| | | | | | |

Представлено до R2006a

Документация Wavelet Toolbox

Поддержка