Q-фактор вейвлета преобразовывает, отношение центральной частоты к полосе пропускания фильтров, используемых в преобразовании. Настраиваемый вейвлет Q-фактора преобразовывает (TQWT) является методом, который создает анализ мультиразрешения вейвлета (MRA) с заданным пользователями Q-фактором. TQWT обеспечивает совершенную реконструкцию сигнала. Коэффициенты TQWT делят энергию сигнала в поддиапазоны.
TQWT был разработан Selesnick [1]. Фильтры использования алгоритма, заданные непосредственно в частотном диапазоне и, могут быть эффективно реализованы с помощью БПФ. Вейвлеты удовлетворяют свойству системы координат Parseval. TQWT задан двумя переменными: Q-фактор и сокращение, также известное как уровень сверхдискретизации. Чтобы получить вейвлеты, хорошо локализованные вовремя, Selesnick рекомендует сокращению r ≥ 3. Как реализовано, tqwt, itqwt, и tqwtmra функции используют фиксированное сокращение r = 3.
Использование дискретного вейвлета преобразовывает (DWT) фиксированный Q-фактор √2. Значение √2 следует из определения MRA, ведущего к ортогональному вейвлету, преобразовывают. Однако в зависимости от данных, другие Q-факторы могут быть желательными. Более высокие Q-факторы приводят к более узким фильтрам, которые лучше для анализа колебательных сигналов. Чтобы анализировать сигналы с переходными компонентами, понизьтесь, Q-факторы являются более соответствующими.
Основной компонент TQWT масштабируется в частотном диапазоне:
масштабирование lowpass — частотный диапазон, масштабирующийся, который сохраняет низкочастотное содержимое
highpass, масштабирующийся — частотный диапазон, масштабирующийся, который сохраняет высокочастотное содержимое
Когда вы масштабируете x сигнала (n), который производится на уровне f s в частотном диапазоне, вы изменяете частоту дискретизации выходного сигнала y (n). Если X (ω) и Y (ω) является преобразованиями Фурье дискретного времени x (n) и y (n), соответственно, и 0 <α <1, lowpass, масштабирующийся α (LPS α) в частотном диапазоне, задан как
Для масштабирования lowpass выходной сигнал производится в α·f s. Если 0 <β ≤ 1, highpass масштабирование β (HPS β) задан как
Для масштабирования highpass выходной сигнал производится в β·f s. Подобные определения существуют для случаев α> 1 и β> 1.
Алгоритм TQWT реализован как двухканальный набор фильтров. В аналитическом направлении поддиапазон lowpass v 0 (n) имеет частоту дискретизации α·f s и highpass поддиапазон, v 1 (n) имеет частоту дискретизации β·f s. Мы говорим, что набор фильтров сверхдискретизирован на коэффициент α + β.
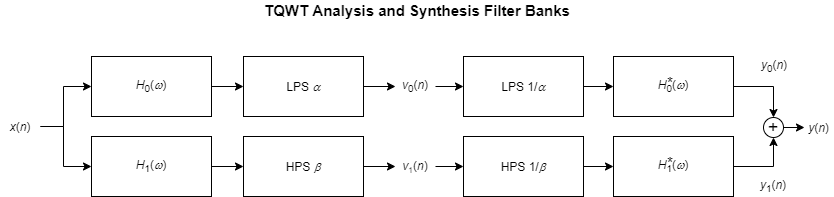
Lowpass и фильтры highpass, H 0 (ω) и H 1 (ω) соответственно, удовлетворяют
и
В алгоритме TQWT аналитический набор фильтров применяется итеративно к выходу lowpass предыдущей итерации. Частотой дискретизации highpass выход в k th итерация является β · αk-1· f s, где f s является частотой дискретизации исходного входного сигнала. Чтобы гарантировать совершенную реконструкцию и хорошо локализованный (вовремя) вейвлеты, алгоритм TQWT требует, чтобы α и β удовлетворили α + β> 1.
В TQWT, и . Как указано выше частота дискретизации в k-ом ieration , где исходная частота дискретизации. В то время как итерации продолжаются, частота дискретизации сходится к Количество сокращение TQWT. Поддержка частотной характеристики k-ой итерации фильтра highpass, , находится в интервале . Центральная частота из highpass фильтр приблизительно равен среднему значению частот в концах интервала: . Полоса пропускания длина интервала: . Q-фактор .
Проиллюстрировать, как сокращение и Q-фактор влияют на полосы перехода lowpass и фильтров highpass, и соответственно, используйте функцию помощника helperPlotLowAndHighpassFilters построить частотные характеристики фильтров для различных значений сокращения и Q-фактора. Исходный код для функции помощника находится в той же директории как этот файл в качестве примера. Функция помощника использует фильтры на основе частотной характеристики Daubechies: для . Для получения дополнительной информации см. [1].
qualityFactor =2; сокращение =
3; helperPlotLowAndHighpassFilters (qualityFactor, сокращение)

Как реализовано, tqwt, itqwt, и tqwtmra функции используют фиксированное сокращение 3. Чтобы видеть, как Q-фактор влияет на вейвлет, используйте функцию помощника helperPlotQfactorWavelet построить вейвлет во временном интервале для различных целочисленных значений Q-фактора. Заметьте, что для фиксированного Q-фактора, уменьшения поддержки вейвлета, когда шкала становится более прекрасной. Для анализа колебательных сигналов более высокие Q-факторы лучше.
qf =1; масштабируйтесь =
8; helperPlotQfactorWavelet (QF, шкала)
9

Загрузите и постройте запись женщины-спикера, говорящей, что "Я видел овец". Частота дискретизации составляет 22 050 Гц.
load wavsheep plot(tsh,sheep) axis tight title('"I saw the sheep."') xlabel("Time (sec)") ylabel("Amplitude")

Получите TQWT использование добротности по умолчанию 1.
[wt1,info1] = tqwt(sheep);
Выход info1 массив структур, который содержит информацию о TQWT. Поле CenterFrequencies содержит нормированные центральные частоты (циклы/выборка) поддиапазонов вейвлета. Поле Bandwidths содержит аппроксимированные полосы пропускания поддиапазонов вейвлета в нормированной частоте. Для каждого поддиапазона подтвердите, что отношение центральной частоты к полосе пропускания равно добротности.
ratios = info1.CenterFrequencies./info1.Bandwidths; [min(ratios) max(ratios)]
ans = 1×2
1 1
Отображение , highpass масштабный коэффициент, и , масштабный коэффициент lowpass. Как реализовано, функции tqwt, itqwt, и tqwtmra используйте фактор сокращения . Подтвердите, что масштабные коэффициенты удовлетворяют отношению .
[info1.Beta info1.Alpha]
ans = 1×2
1.0000 0.6667
r = info1.Beta/(1-info1.Alpha)
r = 3.0000
Идентифицируйте поддиапазоны, которые содержат по крайней мере 15% полной энергии. Обратите внимание на то, что последний элемент wt1 содержит коэффициенты поддиапазона lowpass. Подтвердите, что сумма процентов равняется 100.
EnergyBySubband = cellfun(@(x)norm(x,2)^2,wt1)./norm(sheep,2)^2*100; idx15 = EnergyBySubband >= 15; bar(EnergyBySubband) title("Percent Energy By Subband") xlabel("Subband") ylabel("Percent Energy")

sum(EnergyBySubband)
ans = 100.0000
Получите анализ мультиразрешения и суммируйте те компоненты MRA, соответствующие ранее идентифицированным поддиапазонам.
mra = tqwtmra(wt1,length(sheep)); ts = sum(mra(idx15,:)); plot(tsh,[sheep ts']) axis tight legend("Signal","Large Energy Components") xlabel("Time (sec)") ylabel("Amplitude")

Постройте первый поддиапазон. Заметьте, что этот поддиапазон содержит содержимое частоты слов, "видел" и "овцы".
mra = tqwtmra(wt1,length(sheep)); str = sprintf("Center Frq = %.2f Hz\nBandwidth = %.2f Hz",... fs*info1.CenterFrequencies(1),fs*info1.Bandwidths(1)); plot(tsh,sheep) hold on plot(tsh,mra(1,:)); hold off axis tight title(str) legend("Signal","Subband 1") xlabel("Time (sec)") ylabel("Amplitude")

Чтобы получить более прекрасный вид первого поддиапазона, получите второй TQWT сигнала с помощью добротности 3. Смотрите центральные частоты, в герц, первых пяти поддиапазонов.
[wt3,info3] = tqwt(sheep,QualityFactor=3); fs*info3.CenterFrequencies(1:5)
ans = 1×5
103 ×
8.2688 6.8906 5.7422 4.7852 3.9876
Центральные частоты первых трех поддиапазонов выше, чем центральная частота первого поддиапазона первого TQWT. Получите MRA сигнала с помощью добротности 3 и постройте первые три компонента MRA. Сравните содержимое частоты слов "видело" и "овцы" в этих трех поддиапазонах. Большая часть энергии в первом поддиапазоне прибывает из слова, "видел".
mra = tqwtmra(wt3,length(sheep),QualityFactor=3); for k=1:3 str = sprintf("Center Frq = %.2f Hz",fs*info3.CenterFrequencies(k)); subplot(3,1,k) plot(tsh,mra(k,:)) axis tight title(str) ylabel("Amplitude") end xlabel("Time (sec)")

Постройте процент полной энергии, которую содержит каждый поддиапазон, когда добротность равняется 3. Подтвердите, что сумма процентов равняется 100.
EnergyBySubband = cellfun(@(x)norm(x,2)^2,wt3)./norm(sheep,2)^2*100; figure bar(EnergyBySubband) title("Percent Energy By Subband") xlabel("Subband") ylabel("Percent Energy")

sum(EnergyBySubband)
ans = 100.0000
[1] Selesnick, Иван В. “Преобразование вейвлета С Настраиваемым Q-фактором”. Транзакции IEEE на Обработке сигналов 59, № 8 (август 2011): 3560–75. https://doi.org/10.1109/TSP.2011.2143711.
[2] Daubechies, Ингрид. Десять лекций по вейвлетам. CBMS-NSF региональный ряд конференции в прикладной математике 61. Филадельфия, Па: общество промышленной и прикладной математики, 1992.