Декодируйте код Рида-Соломона, чтобы восстановить бинарные векторные данные
Communications Toolbox / Выявление ошибок и Коррекция / Блок
Блок Binary-Output RS Decoder восстанавливает вектор двоичного сообщения с бинарного вектора кодовой комбинации Тростника-Solomon. Для соответствующего декодирования значения параметров в этом блоке должны совпадать со значениями параметров в соответствующем блоке Binary-Input RS Encoder.
Символы для кода являются двоичными последовательностями длины M, соответствуя элементам Поля Галуа GF (2M). Первый бит в каждом символе является старшим значащим битом.
Этот рисунок показывает размер слова ввода - вывода декодера для длины кодовой комбинации N =7 и размер слова сообщения K =2. Начиная с N =2M– 1, когда N =7, длина символа, M =3.
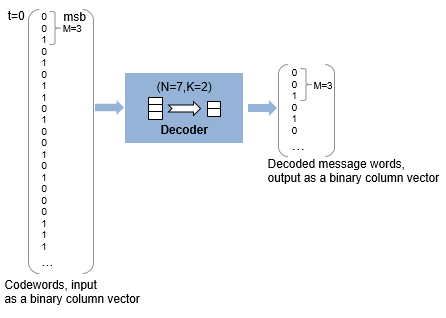
Каждая входная кодовая комбинация является бинарным вектором из длины 21, который представляет 7 трехбитных целых чисел. Каждое соответствующее слово выходного сигнала является бинарным вектором из длины 6, который представляет 2 трехбитных целых числа. Для получения дополнительной информации смотрите Длину сигнала Ввода и вывода в Блоках RS.
Этот значок показывает все порты, включая дополнительные единицы: ![]()
In — Кодовая комбинация тростника-SolomonКодовая комбинация тростника-Solomon в битах в виде (N C× (N – K + S – P) ×M)-by-1 вектор столбца двоичных данных. N C является количеством кодовых комбинаций, N является Codeword length N (symbols), K является Message length K (symbols), S является Shortened message length S (symbols), P является количеством проколов на кодовую комбинацию, и M является количеством битов на символ.
Для получения дополнительной информации смотрите Длину сигнала Ввода и вывода в Блоках RS.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)
Era — Вектор стиранияВектор стирания в символах в виде (N C× (N – K + S – P))-by-1 вектор столбца двоичных данных. N C является количеством кодовых комбинаций, N является Codeword length N (symbols), K является Message length K (symbols), S является Shortened message length S (symbols), P является количеством проколов на кодовую комбинацию, и M является количеством битов на символ.
Значения стирания 1 соответствуют стертым битам в том же положении в кодовой комбинации. Значения 0 соответствуют вдребезги, которые не стираются. Для получения дополнительной информации смотрите Прокалывание и Стирания.
Чтобы включить этот порт, выберите Enable erasures input port.
Типы данных: double | Boolean
Out — Декодируемое сообщениеДекодируемое сообщение в битах, возвращенных как одно из следующего:
Когда нет никакого сокращения сообщения, (N C×K×M)-by-1 вектор столбца двоичных данных.
Когда существует сокращение сообщения, (N C×S×M)-by-1 вектор столбца двоичных данных.
N C является количеством слов сообщения, K является Message length K (symbols), M является количеством битов на символ, и S является Shortened message length S (symbols).
Примечание
Количество декодируемых слов сообщения равняется количеству кодовых комбинаций.
Для получения дополнительной информации смотрите Длину сигнала Ввода и вывода в Блоках RS.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)
Err — Декодирование ошибокОшибки декодирования символа, возвращенные как целочисленный вектор с N C элементы, где N C является количеством кодовых комбинаций. Этот порт указывает на количество ошибок символа, обнаруженных во время декодирования каждой кодовой комбинации. Отрицательное целое число указывает, что блок обнаружил больше ошибок, чем это могло откорректировать при помощи заданной схемы кодирования.
Примечание
(N, K) код Рида-Соломона может откорректировать до floor((N-K)/2) ошибки символа (не битовые ошибки) в каждой кодовой комбинации. Когда полученная кодовая комбинация содержит больше, чем (N-K)/2 ошибки символа, отказ декодирования происходит.
Чтобы включить этот порт, выберите Output number of corrected symbol errors.
Типы данных: double
Для получения дополнительной информации смотрите Поддерживаемые Типы данных.
Codeword length N (symbols) — Длина кодовой комбинацииДлина кодовой комбинации в символах в виде целого числа.
Для получения дополнительной информации смотрите Ограничения на M и Длину кодовой комбинации N и Длину сигнала Ввода и вывода в Блоках RS.
Message length K (symbols) — Передайте размер словаПередайте размер слова в символах в виде целого числа в области значений [1, N –2], где N является длиной кодовой комбинации.
Shortened message length S (symbols) — Сокращенный размер слова сообщенияСокращенный размер слова сообщения в символах в виде целого числа, такого, что S ≤ K. Когда Shortened message length S (symbols) <Message length K (symbols), код Рида-Соломона сокращен.
Вы все еще задаете N и значения K для во всю длину (N, K) код, но декодирование сокращено к (N –K+S, S) код.
Чтобы включить этот параметр, выберите Specify shortened message length.
Generator polynomial — Порождающий полиномrsgenpoly(7, 3, [], [], 'double') (значение по умолчанию) | полиномиальный вектор символов | вектор строки двоичных знаков | двоичный файл вектор-строка Галуа Порождающий полином со значениями от 0 до 2M– 1, в порядке убывающей степени в виде одного из следующего:
Полиномиальный вектор символов. Для получения дополнительной информации смотрите Представление Полиномов в Communications Toolbox.
Целочисленный вектор-строка, который представляет коэффициенты порождающего полинома в порядке убывающей степени.
Целочисленный вектор-строка Галуа, который представляет коэффициенты порождающего полинома в порядке убывающей степени.
Каждый коэффициент является элементом Поля Галуа, заданного примитивным полиномом. Для получения дополнительной информации смотрите, Задают Порождающий полином.
Пример: [1 3 1 2 3], который эквивалентен rsgenpoly(7,3)
Чтобы включить этот параметр, выберите Specify generator polynomial.
Primitive polynomial — Примитивный полином'X^3 + X + 1' (значение по умолчанию) | полиномиальный вектор символов | вектор строки двоичных знаковПримитивный полином в порядке убывающей степени. Этот полином имеет порядок M и задает конечное поле Галуа GF (2M) соответствие целым числам, которые формируют слова сообщения и кодовые комбинации. Задайте примитивный полином как одно из следующего:
Полиномиальный вектор символов. Для получения дополнительной информации смотрите Представление Полиномов в Communications Toolbox.
Вектор строки двоичных знаков, который представляет коэффициенты порождающего полинома.
Для получения дополнительной информации смотрите Ограничения на M и Длину кодовой комбинации N.
Пример: 'X^3 + X + 1', который является примитивным полиномом, используемым для (7,3) код, ppoly = primpoly(3,'nodisplay'); int2bit(ppoly,ceil(log2(max(ppoly))))'
Чтобы включить этот параметр, выберите Specify primitive polynomial.
Puncture vector — Вектор прокола[ones(2,1); zeros(2,1)] (значение по умолчанию) | вектор столбца двоичных данныхВектор прокола в виде (N –K)-by-1 вектор столбца двоичных данных. Индексы элемента с 1s представляют данные индексы symbol, которые проходят через неизменный блок. Индексы элемента с 0s представляют данные индексы symbol, которые проколоты или удалили от потока данных. Для получения дополнительной информации смотрите Прокалывание и Стирания.
Чтобы включить этот параметр, выберите Punctured code.
Enable erasures input port — Включите входной порт стиранийУстановка этого флажка включает порт стираний, Era. Для получения дополнительной информации смотрите Прокалывание и Стирания.
Output number of corrected symbol errors — Позвольте порту вывести количество откорректированных ошибок символаУстановка этого флажка включает дополнительный выходной порт, Err, который указывает на количество ошибок символа блок, откорректированный во входной кодовой комбинации.
Output data type — Выходной тип блокаSame as input (значение по умолчанию) | boolean | doubleВыходной тип блока в виде Same as input, boolean, или double.
Код Рида-Соломона имеет размер слова сообщения, K, или сокращенный размер слова сообщения, S. Длиной кодовой комбинации является N – K + S – P, где N является полной длиной кодовой комбинации, и P является количеством проколов на кодовую комбинацию. Когда нет никакого сокращения сообщения, выражение длины кодовой комбинации уменьшает до N – P, потому что K = S. Если декодер обрабатывает несколько кодовых комбинаций на систему координат, то тот же шаблон прокола содержит для всех кодовых комбинаций.
Эта таблица обеспечивает выражения для длин сигнала ввода и вывода для энкодера Тростника-Solomon и декодера.
Обозначение y = N C × x обозначает, что y является целочисленным кратным x.
| Введите, стирание и длины выходного вектора | ||
|---|---|---|
| Кодер блока RS | Никакое используемое сокращение сообщения | Передайте используемое сокращение |
|
Двоичный вход энкодер RS |
Введите длину (биты): N C × K × M Выведите длину (биты): N C × (N –P) × M |
Введите длину (биты): N C × S × M Выведите длину (биты): N C × (N –K+S–P) × M |
|
Двоичный выход декодер RS |
Введите длину (биты): N C × (N –P) × M Длина стираний (символы): N C × (N –P) Выведите длину (биты): N C × K × M |
Введите длину (биты): N C × (N –K+S–P) × M Длина стираний (символы): N C × (N –K+S–P) Выведите длину (биты): N C × S × M |
N является длиной кодовой комбинации.
K является размером слова сообщения.
S является сокращенным размером слова сообщения.
N C является количеством кодовых комбинаций (и слова сообщения).
P является количеством проколов на кодовую комбинацию и равен количеству нулей в векторе прокола.
M является степенью примитивного полинома. Каждая группа битов M представляет целое число между 0 и 2M–1 это принадлежит конечному полю Галуа GF (2M).
Для получения дополнительной информации о представлении данных для кодов Рида-Соломона смотрите Целочисленный формат (Только Тростник-Solomon).
Кроме того, смотрите Ограничения на M и Длину кодовой комбинации N.
Если вы не выбираете Specify primitive polynomial, допустимые значения для длины кодовой комбинации, N, от 7 до 65 535. В этом случае блок использует примитивный полином по умолчанию степени M = ceil(log2(N+1)). Можно отобразить примитивный полином по умолчанию путем выполнения primpoly(ceil(log2(N+1))).
Если вы выбираете Specify primitive polynomial, допустимые значения для примитивной полиномиальной степени, M, от 3 до 16. Допустимые значения для N в этом случае от 7 до 2M– 1. Выбор Specify primitive polynomial позволяет вам задать примитивный полином, который задает конечное поле GF (2M), который соответствует значениям, которые формируют слова сообщения и кодовые комбинации.
Выберите Specify generator polynomial, чтобы включить параметр Generator polynomial для определения порождающего полинома кода Рида-Соломона. Введите целочисленный вектор-строку со значениями элемента от 0 до 2M- 1. Вектор представляет полином, в порядке убывания степеней, коэффициенты которых являются элементами GF (2M) представленный в целочисленном формате. Для получения дополнительной информации о целочисленном и двоичном формате, смотрите Целочисленный формат (Только Тростник-Solomon). Порождающий полином должен быть равен полиному с этой учтенной формой:
g (x) = (x +αb) (x +αb+1) (x +αb+2)... (x +αb+N-K-1)
α является примитивным элементом Поля Галуа, по которому задан входной сигнал, и b является целым числом.
Если вы не выбираете Specify generator polynomial, блок использует порождающий полином по умолчанию, соответствуя b=1, для кодирования Тростника-Solomon. Можно отобразить порождающий полином по умолчанию путем выполнения rsgenpoly.
Если вы используете примитивный полином по умолчанию (Specify primitive polynomial не выбран), порождающим полиномом по умолчанию является rsgenpoly(N,K), где N = 2M-1.
Если вы не используете примитивный полином по умолчанию (Specify primitive polynomial выбран), и вы задаете примитивный полином как poly, порождающим полиномом является rsgenpoly(N,K,poly).
Примечание
Степенью порождающего полинома является N − K, где N является длиной кодовой комбинации, и K является размером слова сообщения.
1s и 0s имеют точно противоположные значения для векторов стирания и прокола.
В векторе прокола,
1 средние значения, что символ данных передается через неизменный блок.
0 средние значения, что символ данных должен быть проколот или удален от потока данных.
В векторе стирания,
1 средние значения, что символ данных должен быть заменен символом стирания.
0 средние значения, что символ данных передается через неизменный блок.
Эти соглашения применяются и к энкодеру и к декодеру. Для получения дополнительной информации смотрите Сокращение, Прокалывание и Стирания.
| Порт | Поддерживаемые типы данных |
|---|---|
| \in |
|
| |
| Эра |
|
| Допустить ошибку |
|
Этот блок использует Berlekamp-Massey декодирование алгоритма. Для получения информации об этом алгоритме см. Алгоритмы для BCH и RS Декодирование Только для ошибок.
[1] Ивовый прут, системы контроля ошибок Стивена Б. для цифровой связи и устройства хранения данных. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1995.
[2] Berlekamp, Элвин Р. Алгебраическая теория кодирования. Нью-Йорк: McGraw-Hill, 1968.
[3] Кларк, Джордж К. младший и J. Затвор Каин. Кодирование с коррекцией ошибок для цифровой связи. Нью-Йорк: нажатие пленума, 1981.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.