Адаптивно настройте усиление для постоянного уровня сигнала выход
comm.AGC Система object™ создает автоматический контроллер усиления (AGC), который адаптивно настраивает ее усиление, чтобы достигнуть постоянного уровня сигнала при выходе. Для получения дополнительной информации смотрите AGC Логарифмического Цикла. Этот объект спроектирован для потоковой передачи приложений. Для получения дополнительной информации смотрите Советы.
Адаптивно настраивать усиление для постоянного уровня сигнала при выходе:
Создайте comm.AGC объект и набор его свойства.
Вызовите объект с аргументами, как будто это была функция.
Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты?
agc = comm.AGC
agc = comm.AGC(Name,Value)AdaptationStepSize', 0,05 набора размер шага для усиления обновляются к 0,05.
Если в противном случае не обозначено, свойства являются ненастраиваемыми, что означает, что вы не можете изменить их значения после вызова объекта. Объекты блокируют, когда вы вызываете их, и release функция разблокировала их.
Если свойство является настраиваемым, можно изменить его значение в любое время.
Для получения дополнительной информации об изменении значений свойств смотрите Разработку системы в MATLAB Используя Системные объекты.
AdaptationStepSize — Размер шага для обновлений усиленияРазмер шага для усиления обновляется в виде положительной скалярной величины. Увеличение размера шага позволяет AGC более быстро ответить на изменения на уровне входного сигнала, но изменение увеличений уровня выходного сигнала после достижения установившейся операции. Для получения дополнительной информации смотрите Критерии Эффективности AGC, и Варьироваться Размер Шага AGC и Эффект Графика Размера Шага на примерах Эффективности AGC.
Настраиваемый: да
Типы данных: double
DesiredOutputPower — Целевой уровень выходной мощностиЦелевой уровень выходной мощности в виде положительной скалярной величины. Степень измеряется в Уоттсе, на которого ссылаются к 1 Ому. Для получения дополнительной информации смотрите, Адаптивно Настраивают Полученную Амплитуду Сигнала Используя пример AGC.
Типы данных: double
AveragingLength — Продолжительность усреднения окнаДлина окна усреднения в выборках в виде положительного целого числа. Для получения дополнительной информации о том, как продолжительность усреднения влияет на отклонение выходного сигнала AGC в установившейся операции и скорости выполнения, смотрите Советы и Варьироваться AGC, Составляющий в среднем пример Длины.
Типы данных: double
MaxPowerGain — Усиление максимальной мощностиУсиление максимальной мощности в децибелах в виде положительной скалярной величины. Большие корректировки усиления могут вызвать усечение, когда маленькая степень входного сигнала внезапно увеличивается. Используйте это свойство избежать больших корректировок усиления путем ограничения усиления, что AGC применяется к входному сигналу. Для получения дополнительной информации смотрите Изменять Усиление Максимума AGC и Продемонстрируйте Эффект Максимального Усиления AGC на Пакетных примерах Данных.
Типы данных: double
y = agc(x)
[ возвращает y,powerlevel] = agc(x)powerlevel, оценка уровня мощности входного сигнала. Можно использовать powerlevel когда энергетический детектор выводится.
x — Входной сигналВходной сигнал в виде вектор-столбца.
Типы данных: single | double
Поддержка комплексного числа: Да
y — Выходной сигналВыходной сигнал, возвращенный как вектор-столбец. Выходной сигнал является совпадающим типом данных как входным сигналом, x.
powerlevel — Оценка уровня мощностиОценка уровня мощности, возвращенная как вектор-столбец S-элемента N. N S является длиной входного сигнала, x. Можно использовать powerlevel когда энергетический детектор выводится.
Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:
release(obj)
Примените различные продолжительности усреднения AGC к QAM-модулируемым сигналам. Сравните отклонение и график сигналов после того, как AGC будет применен.
Создайте три Системных объекта AGC с их средним набором длин окна к 10, 100, и 1 000 выборок, соответственно.
agc1 = comm.AGC('AveragingLength',10); agc2 = comm.AGC('AveragingLength',100); agc3 = comm.AGC('AveragingLength',1000);
Сгенерируйте 16-QAM модулируемый и повышенный косинус packetized данные импульсной формы.
M = 16; d = randi([0 M-1],1000,1); s = qammod(d,M); x = 0.1*s; pulseShaper = comm.RaisedCosineTransmitFilter; y = awgn(pulseShaper(x),inf);
Примените AGC к данным, получив отдельные выходные параметры для каждого объекта AGC.
r1 = agc1(y); r2 = agc2(y); r3 = agc3(y);
Постройте и сравните сигналы. Когда продолжительность усреднения увеличивается, отклонение при выходе уменьшений AGC.
figure(1) subplot(4,1,1) plot(abs(y)) title('AGC Input') subplot(4,1,2) plot(abs(r1)) axis([0 8000 0 10]) title('AGC Output (Averaging Length is 10 Samples)') text(4000,5,sprintf('Variance is %f',var(r1(3000:end)))) subplot(4,1,3) plot(abs(r2)) axis([0 8000 0 10]) title('AGC Output (Averaging Length is 100 Samples)') text(4000,5,sprintf('Variance is %f',var(r2(3000:end)))) subplot(4,1,4) plot(abs(r3)) axis([0 8000 0 10]) title('AGC Output (Averaging Length is 1000 Samples)') text(4000,5,sprintf('Variance is %f',var(r3(3000:end))))

Примените различные уровни усиления максимума AGC к модулируемым QPSK сигналам. Сравните график сигналов после того, как AGC будет применен.
Создайте три Системных объекта AGC с их максимальным набором значений усиления к 10, 20, и 30 дБ, соответственно.
agc1 = comm.AGC('MaxPowerGain',10); agc2 = comm.AGC('MaxPowerGain',20); agc3 = comm.AGC('MaxPowerGain',30);
Сгенерируйте модулируемые QPSK данные. Передайте данные через повышенный косинус фильтрация импульсной формы и канал AWGN.
M = 4; pktLen = 10000; d = randi([0 M-1],pktLen,1); s = pskmod(d,M,pi/4); x = repmat([zeros(pktLen,1); 0.3*s],3,1); pulseShaper = comm.RaisedCosineTransmitFilter; y = awgn(pulseShaper(x),50);
Примените AGC к данным, получив отдельные выходные параметры для каждого объекта AGC.
r1 = agc1(y); r2 = agc2(y); r3 = agc3(y);
Постройте входной сигнал и настроенный AGC сигнал с различными максимальными уровнями усиления. Сравните результаты для условий в этом примере.
Максимальная установка усиления 10 дБ слишком мала, и AGC, выход не достигает желаемого уровня выходного сигнала, рискуя потерей данных из-за уменьшенного динамического диапазона сигнала.
Максимальная установка усиления 20 дБ оптимальна, и AGC, выход достигает желаемого уровня без потери сигнала из-за насыщения.
Максимальная установка усиления 30 дБ является слишком большой, и AGC, выход промахивается по желаемому уровню сигнала, рискуя насыщением сигнала и потерей данных в начале полученных пакетов.
Между пакетами входной сигнал содержит только шум.
Как показано в графиках, пакетные передачи имеют длительные периоды, когда никакие данные не получены. Длительные периоды без данных получили результаты в AGC, увеличивающемся до максимальной установки усиления. Если пакет прибывает, когда усиление AGC слишком высоко, выходная мощность промахивается по желаемому уровню сигнала, пока AGC не может ответить на изменение на уровне входной мощности и уменьшать его усиление.
limits = [0 3]; figure(1) subplot(4,1,1) plot(abs(y)) ylim(limits) title('AGC Input') subplot(4,1,2) plot(abs(r1)) ylim(limits) title('AGC Output (Maximum Power Gain is 10 dB)') subplot(4,1,3) plot(abs(r2)) ylim(limits) title('AGC Output (Maximum Power Gain is 20 dB)') subplot(4,1,4) plot(abs(r3)) ylim(limits) title('AGC Output (Maximum Power Gain is 30 dB)')

Постройте сигнал и оценку уровня мощности. Сравнение результатов. Оценка уровня мощности может служить детектором степени, указывая точно, когда полученный пакет прибыл.
Создайте Системный объект AGC с его максимальным набором значений усиления к 20 дБ.
agc20 = comm.AGC('MaxPowerGain',20);Сгенерируйте модулируемые QPSK данные. Передайте данные через повышенный косинус фильтрация импульсной формы и канал AWGN.
modOrd = 4; % Modulation order pktLen = 10000; % Packet length d = randi([0 modOrd-1],pktLen,1); s = pskmod(d,modOrd,pi/4); x = repmat([zeros(pktLen,1); 0.3*s],3,1); pulseShaper = comm.RaisedCosineTransmitFilter; y = awgn(pulseShaper(x),50);
Примените AGC к данным, получив отдельные выходные параметры для каждого объекта AGC.
[r2,p2] = agc20(y);
Постройте входной сигнал и оценку уровня принимаемой мощности сигнала. Сравнение результатов. Прием packetized данных с длительными периодами, когда никакие данные не получены результаты в обнаруженной оценке уровня мощности, уменьшающейся почти к нулю. В то время как входной сигнал обнаруживается, оценка уровня выходной мощности, p2, служит детектором степени, указывая точно, когда полученный пакет прибыл.
limits = [0 3]; figure(1) subplot(4,1,1) plot(abs(y)) ylim(limits) title('AGC Input') subplot(4,1,2) plot(abs(p2)) title('Power Level')

Примените различные размеры шага AGC к модулируемым QPSK сигналам. Сравните сигналы после применения AGC.
Создайте три Системных объекта AGC с их набором размеров шага к 1e-1, 1e-3, и 1e-4, соответственно.
agc1 = comm.AGC('AdaptationStepSize',1e-1); agc2 = comm.AGC('AdaptationStepSize',1e-3); agc3 = comm.AGC('AdaptationStepSize',1e-4);
Сгенерируйте модулируемые QPSK данные с повышенным формированием импульса косинуса.
d = randi([0 3],500,1); s = pskmod(d,4,pi/4); x = 0.1*s; pulseShaper = comm.RaisedCosineTransmitFilter; y = pulseShaper(x);
Примените AGC к данным, получив отдельные выходные параметры для каждого объекта AGC.
r1 = agc1(y); r2 = agc2(y); r3 = agc3(y);
Постройте сигнал ввода и вывода после различных размеров шага AGC.
С набором размера шага к 1e-1 перерегулирование выходного сигнала AGC очевидно. Выходной сигнал сходится очень быстро.
С набором размера шага к 1e-3 исчезает перерегулирование выходного сигнала AGC. Выходной сигнал постепенно сходится.
С набором размера шага к 1e-4 выходной сигнал AGC берет в 2 - 3 раза дольше, чтобы сходиться, чем размер шага 1e-3.
figure subplot(4,1,1) plot(abs(y)) title('AGC Input') subplot(4,1,2) plot(abs(r1)) title('AGC Output (Adaption Step Size is 1e-1)') subplot(4,1,3) plot(abs(r2)) title('AGC Output (Adaption Step Size is 1e-3)') subplot(4,1,4) plot(abs(r3)) title('AGC Output (Adaption Step Size is 1e-4)')

Модулируйте и усильте сигнал QPSK. Установите полученную амплитуду сигнала приблизительно на 1 вольт при помощи AGC. Постройте выход.
Создайте модулируемый QPSK сигнал при помощи Системного объекта QPSK.
data = randi([0 3],1000,1); qpsk = comm.QPSKModulator; modData = qpsk(data);
Ослабьте модулируемый сигнал.
txSig = 0.1*modData;
Создайте Системный объект AGC и передайте переданный сигнал через него. AGC настраивает принимаемую мощность сигнала приблизительно к 1 Вт.
agc = comm.AGC; rxSig = agc(txSig);
Постройте сигнальные созвездия передачи и полученных сигналов после того, как AGC достигнет установившийся.
h = scatterplot(txSig(200:end),1,0,'*'); hold on scatterplot(rxSig(200:end),1,0,'or',h); legend('Input of AGC','Output of AGC')

Измерьте и сравните степень переданных и полученных сигналов после того, как AGC достигнет устойчивого состояния. Степень переданного сигнала в 100 раз меньше, чем степень полученного сигнала.
txPower = var(txSig(200:end)); rxPower = var(rxSig(200:end)); [txPower rxPower]
ans = 1×2
0.0100 0.9970
Создайте две Системы AGC objects™, чтобы настроить уровень полученного сигнала с помощью двух различных размеров шага с идентичными периодами обновления.
Сгенерируйте сигнал 8-PSK, таким образом, что его степень составляет 10 Вт.
data = randi([0 7],200,1);
modData = sqrt(10)*pskmod(data,8,pi/8,'gray');Создайте пару повышенных согласованных фильтров косинуса с их Gain набор свойств так, чтобы у них была выходная мощность единицы.
txfilter = comm.RaisedCosineTransmitFilter('Gain',sqrt(8)); rxfilter = comm.RaisedCosineReceiveFilter('Gain',sqrt(1/8));
Пропустите модулируемый сигнал через повышенный фильтр передачи косинуса.
txSig = txfilter(modData);
Создайте два Системных объекта AGC, чтобы настроить полученный уровень сигнала. Установите размер шага 0,01 и 0.1, соответственно.
agc1 = comm.AGC('AdaptationStepSize',0.01); agc2 = comm.AGC('AdaptationStepSize',0.1);
Примените AGC к модулируемому сигналу, получив отдельные выходные параметры для каждого объекта AGC.
agcOut1 = agc1(txSig); agcOut2 = agc2(txSig);
Фильтр выходные сигналы AGC при помощи повышенного косинуса получает фильтр.
rxSig1 = rxfilter(agcOut1); rxSig2 = rxfilter(agcOut2);
Постройте степень отфильтрованных ответов AGC, в то время как составление 10 задержек символа через передачу - получает пару фильтра.
plot([abs(rxSig1(11:110)).^2 abs(rxSig2(11:110)).^2]) grid on xlabel('Symbols') ylabel('Power (W)') legend('Step size 0.01','Step size 0.1')

Сигнал с большим размером шага сходится быстрее к целевому уровню мощности AGC 1 Вт.
Постройте степень установившихся отфильтрованных сигналов AGC включением только последних 100 символов. Больший размер шага AGC приводит к менее точной коррекции усиления. Большие значения размера шага AGC приводят к более быстрой сходимости за счет менее точного управления усилением.
plot((101:200),[abs(rxSig1(101:200)).^2 abs(rxSig2(101:200)).^2]) grid on xlabel('Symbols') ylabel('Power (W)') legend('Step size 0.01','Step size 0.1')

Передайте ослабленные пакетные данные о QPSK двум AGCs с различными максимальными усилениями. Постройте график результатов.
Создайте два, пакеты данных QSPK с 200 символами. Передайте пакеты по системе координат с 1200 символами.
modData1 = pskmod(randi([0 3],200,1),4,pi/4); modData2 = pskmod(randi([0 3],200,1),4,pi/4); txSig = [modData1; zeros(400,1); modData2; zeros(400,1)];
Ослабьте переданный пакетный сигнал на 20 дБ и постройте его степень.
rxSig = 0.1*txSig; rxSigPwr = abs(rxSig).^2; plot(rxSigPwr) grid xlabel('Symbols') ylabel('Power (W)') title('Signal Power Before Applying AGC')

Создайте два AGCs с усилениями максимальной мощности 30 дБ и 24 дБ, соответственно.
agc1 = comm.AGC('MaxPowerGain',30,'AdaptationStepSize',0.02); agc2 = comm.AGC('MaxPowerGain',24,'AdaptationStepSize',0.02);
Примените AGC к ослабленному сигналу, получив отдельные выходные параметры для каждого объекта AGC. Вычислите выходную мощность для каждого случая.
rxAGC1 = agc1(rxSig); rxAGC2 = agc2(rxSig); pwrAGC1 = abs(rxAGC1).^2; pwrAGC2 = abs(rxAGC2).^2;
Постройте выходные мощности. Первоначально, для второго пакета, agc1 степень выходного сигнала слишком высока, потому что AGC применил свое максимальное усиление в период, когда никакие данные не были переданы. Соответствующий agc2 степень выходного сигнала (2,5 Вт) промахивается по целевому уровню мощности 1 Вт значительно меньше, чем agc1 степень выходного сигнала (10 Вт). Время сходимости для agc2 короче, чем время сходимости для agc1, потому что вход сигнала к agc2 применяет меньшее максимальное усиление, чем agc1.
plot([pwrAGC1 pwrAGC2]) legend('AGC1','AGC2') grid xlabel('Symbols') ylabel('Power (W)') title('Signal Power After Applying AGC')

Реализация AGC использует логарифмическую обратную связь. Когда этот рисунок Алгоритма AGC логарифмического цикла показывает, выходной сигнал является продуктом входного сигнала и экспоненциалом усиления цикла. Сигнал ошибки является различием между контрольным уровнем и продуктом логарифма детектора выход и экспоненциал усиления цикла. После умножения на размер шага AGC передает сигнал ошибки интегратору.
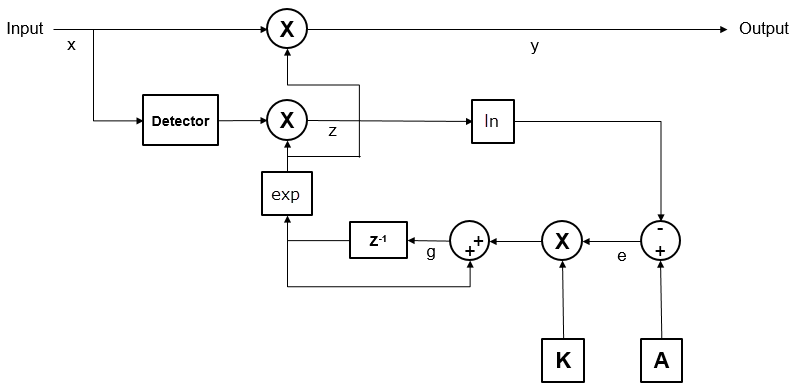
AGC логарифмического цикла выполняет хорошо для множества типов сигнала, включая амплитудную модуляцию. Детектор AGC применяется к входному сигналу, который улучшает время сходимости, но увеличивает изменение степени сигнала во входе детектора. Большое изменение сигнала во входе детектора приемлемо для систем с плавающей точкой.
Математически, алгоритм получен в итоге как
где:
x является входным сигналом.
y является выходным сигналом.
g является усилением цикла.
D(•) является функцией детектора.
z является детектором выход.
A является ссылочным значением.
e является сигналом ошибки.
K является размером шага.
Детектор AGC выход, z, вычисляет квадратичный детектор, данный
где N является периодом обновления. Квадратичный детектор производит выход, пропорциональный квадрату входного сигнала y.
Увеличение размера шага уменьшает время атаки и времена затухания, но это также увеличивает нагнетание усиления.
Время атаки — длительность, взятая для AGC, чтобы ответить на увеличение входной амплитуды
Время затухания — длительность, взятая для AGC, чтобы ответить на уменьшение во входной амплитуде
Получите нагнетание — изменение значения усиления во время установившейся операции
Этот Системный объект спроектирован для потоковой передачи приложений.
Если амплитуда сигнала не изменяется в системе координат, можно симулировать идеальный AGC путем вычисления среднего усиления, желаемого для системы координат выборок. Затем примените усиление к каждой выборке в системе координат.
Если вы используете AGC с высшим порядком сигналы QAM, вы можете должны быть уменьшать изменение усиления во время установившейся операции. Смотрите схему созвездия при выходе AGC во время установившейся операции. Можно увеличить продолжительность усреднения, чтобы избежать частых корректировок усиления. Увеличение усреднения длины уменьшает скорость выполнения.
Указания и ограничения по применению:
Смотрите системные объекты в Генерации кода MATLAB (MATLAB Coder).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.