Integer-Input RS Encoder
Создайте код Рида-Соломона из целочисленных векторных данных
- Библиотека:
Communications Toolbox / Выявление ошибок и Коррекция / Блок
Описание
Блок Integer-Input RS Encoder создает код Рида-Соломона.
Символы для кода являются целыми числами между 0 и 2M- 1, которые представляют элементы конечного поля GF (2M). Значением по умолчанию M является самое маленькое целое число, которое больше или равно log2 (N +1), то есть, ceil(log2(N+1)). Можно изменить значение по умолчанию M путем определения примитивного полинома для GF (2M), как описано в Задают Примитивный Полином ниже. Ограничения на M и N описаны в Ограничениях на M и Длину кодовой комбинации N.
Ввод и вывод является сигналами с целочисленным знаком, которые представляют сообщения и кодовые комбинации, соответственно. Для получения дополнительной информации смотрите Длину сигнала Ввода и вывода в Блоках RS.
(N, K) код Рида-Соломона может откорректировать до floor((N-K)/2) ошибки символа (не битовые ошибки) в каждой кодовой комбинации.
Предположим M = 3, N = 23- 1 = 7, и K = 5. Затем сообщение является вектором из длины 5, чьи записи являются целыми числами между 0 и 7. Соответствующая кодовая комбинация является вектором из длины 7, чьи записи являются целыми числами между 0 и 7. Следующая фигура иллюстрирует возможные сигналы ввода и вывода с этим блоком, когда Codeword length N установлен в 7, Message length K установлен в 5, и примитив по умолчанию и полиномы генератора используются.
Порты
Входной параметр
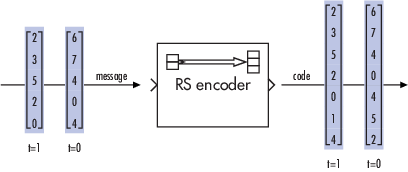
In сообщение
целочисленный вектор-столбец
Обменивайтесь сообщениями в виде одного из следующего:
Когда нет никакого сокращения сообщения, (N C×K)-by-1 целочисленный вектор-столбец.
Когда существует сокращение сообщения, (N C×S)-by-1 целочисленный вектор-столбец.
N C является количеством слов сообщения, K является Message length K, и S является Shortened message length S.
Примечание
Количество декодируемых слов сообщения равняется количеству кодовых комбинаций.
Для получения дополнительной информации смотрите Длину сигнала Ввода и вывода в Блоках RS.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Вывод
Out — Кодовая комбинация тростника-Solomon
целочисленный вектор-столбец
Кодовая комбинация тростника-Solomon, возвращенная как (N C× (N – K + S – P)-by-1 целочисленный вектор-столбец. N C является количеством кодовых комбинаций, N является Codeword length N, K является Message length K, S является Shortened message length S, P является количеством проколов на кодовую комбинацию.
Для получения дополнительной информации смотрите Длину сигнала Ввода и вывода в Блоках RS.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Для получения дополнительной информации смотрите Поддерживаемые Типы данных.
Параметры
Codeword length N — Длина кодовой комбинации
7
Длина кодовой комбинации в виде целого числа.
Для получения дополнительной информации смотрите Ограничения на M и Длину кодовой комбинации N и Длину сигнала Ввода и вывода в Блоках RS.
Message length K — Передайте размер слова
3
Передайте размер слова в виде целого числа в области значений [1, N –2], где N является длиной кодовой комбинации.
Shortened message length S — Сокращенный размер слова сообщения
3
Сокращенный размер слова сообщения в виде целого числа, такого, что S ≤ K. Когда Shortened message length S <Message length K, код Рида-Соломона сокращен.
Вы все еще задаете N и значения K для во всю длину (N, K) код, но декодирование сокращено к (N –K+S, S) код.
Зависимости
Чтобы включить этот параметр, выберите Specify shortened message length.
Generator polynomial — Порождающий полином
rsgenpoly(7, 3, [], [], 'double') (значение по умолчанию) | полиномиальный вектор символов | вектор строки двоичных знаков | двоичный файл вектор-строка Галуа
Порождающий полином со значениями в области значений [от 0 до 2M– 1], в порядке убывающей степени в виде одного из следующего:
Полиномиальный вектор символов. Для получения дополнительной информации смотрите Представление Полиномов в Communications Toolbox.
Целочисленный вектор-строка, который представляет коэффициенты порождающего полинома в порядке убывающей степени.
Целочисленный вектор-строка Галуа, который представляет коэффициенты порождающего полинома в порядке убывающей степени.
Каждый коэффициент является элементом Поля Галуа, заданного примитивным полиномом. Для получения дополнительной информации смотрите, Задают Порождающий полином.
Пример: [1 3 1 2 3], который эквивалентен rsgenpoly(7,3)
Зависимости
Чтобы включить этот параметр, выберите Specify generator polynomial.
Primitive polynomial — Примитивный полином
'X^3 + X + 1' (значение по умолчанию) | полиномиальный вектор символов | вектор строки двоичных знаков
Примитивный полином в порядке убывающей степени. Этот полином имеет порядок M и задает конечное поле Галуа GF (2M) соответствие целым числам, которые формируют слова сообщения и кодовые комбинации. Задайте примитивный полином как одно из следующего:
Полиномиальный вектор символов. Для получения дополнительной информации смотрите Представление Полиномов в Communications Toolbox.
Вектор строки двоичных знаков, который представляет коэффициенты порождающего полинома.
Для получения дополнительной информации смотрите, Задают Примитивный Полином.
Пример: 'X^3 + X + 1', который является примитивным полиномом, используемым для (7,3) код, ppoly = primpoly(3,'nodisplay'); int2bit(ppoly,ceil(log2(max(ppoly))))'
Зависимости
Чтобы включить этот параметр, выберите Specify primitive polynomial.
Puncture vector — Вектор прокола
[ones(2,1); zeros(2,1)] (значение по умолчанию) | вектор столбца двоичных данных
Вектор прокола в виде (N –K)-by-1 вектор столбца двоичных данных. Индексы элемента с 1s представляют данные индексы symbol, которые проходят через неизменный блок. Индексы элемента с 0s представляют данные индексы symbol, которые проколоты или удалили от потока данных. Для получения дополнительной информации смотрите Прокалывание и Стирания.
Примечание
Если энкодер обрабатывает несколько кодовых комбинаций на систему координат, то тот же шаблон прокола содержит для всех кодовых комбинаций.
Зависимости
Чтобы включить этот параметр, выберите Puncture code.
Характеристики блока
Типы данных |
|
Многомерные сигналы |
|
Сигналы переменного размера |
|
Больше о
Длина сигнала ввода и вывода в блоках RS
Код Рида-Соломона имеет размер слова сообщения, K, или сокращенный размер слова сообщения, S. Длиной кодовой комбинации является N – K + S – P, где N является полной длиной кодовой комбинации, и P является количеством проколов на кодовую комбинацию. Когда нет никакого сокращения сообщения, выражение длины кодовой комбинации уменьшает до N – P, потому что K = S. Если декодер обрабатывает несколько кодовых комбинаций на систему координат, то тот же шаблон прокола содержит для всех кодовых комбинаций.
Эта таблица обеспечивает выражения для длин сигнала ввода и вывода для энкодера Тростника-Solomon и декодера.
Обозначение y = N C × x обозначает, что y является целочисленным кратным x.
| Введите, стирание и длины выходного вектора | ||
|---|---|---|
| Кодер блока RS | Никакое используемое сокращение сообщения | Передайте используемое сокращение |
|
Введенный целым числом энкодер RS |
Введите длину (символы): N C × K Выведите длину (символы): N C × (N –P) |
Введите длину (символы): N C × S Выведите длину (символы): N C × (N –K+S–P) |
|
Выведенный целым числом декодер RS |
Введите длину (символы): N C × (N –P) Длина стираний (символы): N C × (N –P) Выведите длину (символы): N C × K |
Введите длину (символы): N C × (N –K+S–P) Длина стираний (символы): N C × (N –K+S–P) Выведите длину (символы): N C × S |
N является длиной кодовой комбинации.
K является размером слова сообщения.
S является сокращенным размером слова сообщения.
N C является количеством кодовых комбинаций (и слова сообщения).
P является количеством проколов и равен количеству нулей в векторе прокола.
M является степенью примитивного полинома. Каждая группа битов M представляет целое число между
0и2M–1это принадлежит конечномуполю Галуа GF (2M).
Для получения дополнительной информации о представлении данных для кодов Рида-Соломона смотрите Целочисленный формат (Только Тростник-Solomon).
Ограничения на M и длину кодовой комбинации N
Если вы не выбираете Specify primitive polynomial, допустимые значения для длины кодовой комбинации, N, от 7 до 65 535. В этом случае блок использует примитивный полином по умолчанию степени
M = ceil(log2(N+1)). Можно отобразить примитивный полином по умолчанию путем выполненияprimpoly(ceil(log2(N+1))).Если вы выбираете Specify primitive polynomial, допустимые значения для примитивной полиномиальной степени, M, от 3 до 16. Допустимые значения для N в этом случае от 7 до 2M– 1. Выбор Specify primitive polynomial позволяет вам задать примитивный полином, который задает конечное поле GF (2M), который соответствует значениям, которые формируют слова сообщения и кодовые комбинации.
Задайте примитивный полином
Можно задать примитивный полином, который задает конечное поле GF (2M), соответствуя целым числам, которые формируют сообщения и кодовые комбинации. Для этого сначала выберите Specify primitive polynomial. Затем в текстовом поле Primitive polynomial введите вектор строки двоичных знаков, который представляет примитивный полином по GF (2M), в порядке убывания степеней. Например, чтобы задать полином x3+x+1, введите векторный [1 0 1 1].
Если вы не выбираете Specify primitive polynomial, блок использует примитивный полином по умолчанию степени M =, перекрывают (log2 (N+1)). Можно отобразить полином по умолчанию путем ввода primpoly(ceil(log2(N+1))) в MATLAB® подсказка.
Задайте порождающий полином
Выберите Specify generator polynomial, чтобы включить параметр Generator polynomial для определения порождающего полинома кода Рида-Соломона. Введите целочисленный вектор-строку со значениями элемента от 0 до 2M- 1. Вектор представляет полином, в порядке убывания степеней, коэффициенты которых являются элементами GF (2M) представленный в целочисленном формате. Для получения дополнительной информации о целочисленном и двоичном формате, смотрите Целочисленный формат (Только Тростник-Solomon). Порождающий полином должен быть равен полиному с этой учтенной формой:
g (x) = (x +αb) (x +αb+1) (x +αb+2)... (x +αb+N-K-1)
α является примитивным элементом Поля Галуа, по которому задан входной сигнал, и b является целым числом.
Если вы не выбираете Specify generator polynomial, блок использует порождающий полином по умолчанию, соответствуя b=1, для кодирования Тростника-Solomon. Можно отобразить порождающий полином по умолчанию путем выполнения rsgenpoly.
Если вы используете примитивный полином по умолчанию (Specify primitive polynomial не выбран), порождающим полиномом по умолчанию является
rsgenpoly(N,K), гдеN = 2M-1.Если вы не используете примитивный полином по умолчанию (Specify primitive polynomial выбран), и вы задаете примитивный полином как
poly, порождающим полиномом являетсяrsgenpoly(N,K,poly).
Примечание
Степенью порождающего полинома является N − K, где N является длиной кодовой комбинации, и K является размером слова сообщения.
Прокалывание и стирания
1s и 0s имеют точно противоположные значения для векторов стирания и прокола.
В векторе прокола,
1
средние значения, что символ данных передается через неизменный блок.0
средние значения, что символ данных должен быть проколот или удален от потока данных.
В векторе стирания,
1
средние значения, что символ данных должен быть заменен символом стирания.0
средние значения, что символ данных передается через неизменный блок.
Эти соглашения применяются и к энкодеру и к декодеру. Для получения дополнительной информации смотрите Сокращение, Прокалывание и Стирания.
Поддерживаемые типы данных
| Порт | Поддерживаемые типы данных |
|---|---|
| \in |
|
|
Парный блок
Алгоритмы
Этот объект реализует алгоритм, входные параметры и выходные параметры, описанные в Алгоритмах для BCH и RS Декодирование Только для ошибок.