Канал AWGN добавляет белый Гауссов шум в сигнал, который проходит через него. Можно создать канал AWGN в модели с помощью comm.AWGNChannel Система object™, блок AWGN Channel, или awgn функция.
Следующие примеры используют Канал AWGN: Передатчик QPSK и Приемник и Общая Модуляция QAM в Канале AWGN.
Типичные количества, используемые, чтобы описать относительную степень шума в канале AWGN, включают
Отношение сигнал-шум (SNR) на выборку. ОСШ является фактическим входным параметром к awgn функция.
Отношение энергии, подведенной к долоту к спектральной плотности мощности шума (EbN0). Это количество используется BER Analyzer Инструмент и оценка результатов деятельности функционируют в этом тулбоксе.
Отношение энергии символа к спектральной плотности мощности шума (EsN0)
Отношение между EsN0 и EbN0, оба описанные в дБ, следующие:
где k является количеством информационных битов на символ.
В системе связи k может быть под влиянием размера алфавита модуляции или скорости кода кода контроля ошибок. Например, в системе с помощью rate-1/2 код и модуляция 8-PSK, количество информационных битов на символ (k) является продуктом скорости кода и количеством закодированных битов на модулируемый символ. А именно, (1/2) log2 (8) = 3/2. В такой системе три информационных бита соответствуют шести закодированным битам, которые в свою очередь соответствуют двум символам 8-PSK.
Отношение между EsN0 и ОСШ, оба описанные в дБ, следующие:
где T sym является символьным периодом сигнала, и маисовая крупа T является периодом выборки сигнала.
Для комплексного сгенерированного модулированного сигнала, сверхдискретизированного на коэффициент 4, EsN0 превышает соответствующий ОСШ на 10 log10 (4).
Деривация для Комплексных Входных сигналов. Можно вывести отношение между EsN0 и ОСШ для комплексных входных сигналов можно следующим образом:
где
S = степень Входного сигнала, в ваттах
N = Шумовая мощность, в ваттах
B n = Шумовая полоса пропускания, в Герц = F s = 1/Tsamp.
F s = Частота дискретизации, в Герц
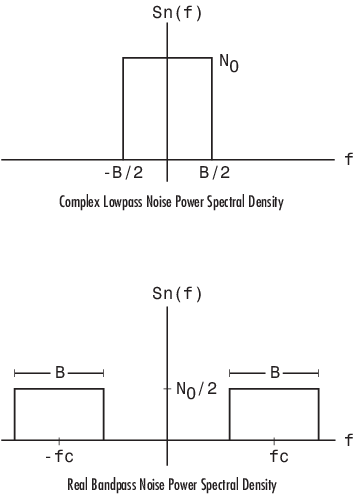
Поведение для Действительных и Комплексных Входных сигналов. Эти фигуры иллюстрируют различие между действительными и комплексными случаями путем показа спектральных плотностей мощности шума действительного полосового процесса белого шума и его комплексного эквивалентного lowpass.