Документация

Что такое чебышевский сплайн?

Чебышевский сплайн C =Ct=C_{k, t} порядка k для последовательности узла t = (t _i: i =1:n+k), уникальный элемент S _{k, t} макс. нормы 1, который максимально колеблется на интервале [t _k.. t _{n +1}] и положителен около t _{n +1}. Это означает, что существует уникальный строго увеличивающийся n - последовательность τ так, чтобы функциональный C =Ct∊S_{k, t}, данный C _(τi) = (–1)^{n – 1}, весь i, имеет макс. норму 1 на [t _k.. t _{n +1}]. Это подразумевает что _τ1=tk, _τn=tn+1, и что t _i <_τi <t _{k +i}, для всего i. На самом деле, t _i+1 ≤ _τi ≤ t _{i +k–1}, весь i. Это поднимает точку, что последовательность узла принята, чтобы сделать такое неравенство возможным, т.е. элементы S _{k, t} принят, чтобы быть непрерывным.

Короче говоря, Чебышевский сплайн взгляды C точно так же, как Полином Чебышева. Это выполняет подобные функции. Например, его экстремальные сайты τ являются особенно хорошими сайтами, чтобы интерполировать в от S _{k, t}, потому что норма получившегося проектора является почти столь маленькой, как может быть; смотрите команду тулбокса chbpnt.

Можно запустить Конструкцию в качестве примера Чебышевского Сплайна, чтобы создать C для конкретной последовательности узла t.

Выбор пробела сплайна

Вы имеете дело с кубическими сплайнами, i.e., с порядком

k = 4;

и используйте последовательность пропуска

breaks = [0 1 1.1 3 5 5.5 7 7.1 7.2 8];
lp1 = length(breaks); 

и используйте простые внутренние узлы, i.e., используйте последовательность узла

t = breaks([ones(1,k) 2:(lp1-1) lp1(:,ones(1,k))]);
n = length(t)-k;

Отметьте четырехкратный узел в каждом конце. Поскольку k = 4, это делает [0.. 8] = [breaks(1).. breaks(lp1)] интервал [t _k.. t _{n +1}] интереса, с n = length(t)K размерность получившегося пробела сплайна S _{k, t}. Та же последовательность узла была бы предоставлена

t=augknt(breaks,k);

Исходное предположение

Как исходное предположение для τ, используйте средние значения узла

рекомендуемый как хороший выбор сайта интерполяции. Они предоставляются

tau=aveknt(t,k); 

Постройте получившееся первое приближение к C, т.е. сплайн c, который удовлетворяет c _(τi) = (–1)^n-–i, весь i:

b = cumprod(repmat(-1,1,n)); b = b*b(end);
c = spapi(t,tau,b); 
fnplt(c,'-.') 
grid

Вот получившийся график.

Итерация Remez

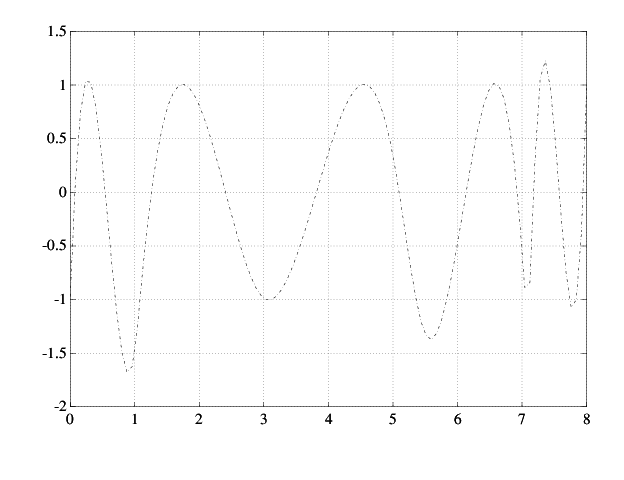
Начиная с этого приближения, вы используете алгоритм Remez, чтобы произвести последовательность сплайнов, сходящихся к C. Это означает, что вы создаете новый τ как экстремальное значение вашего текущего приближения c к C и попробовали еще раз. Вот целый цикл.

Вы находите новую внутреннюю часть _τi как нули Dc, т.е. первая производная c, на нескольких шагах. Во-первых, дифференцируйтесь:

Dc = fnder(c);

Затем возьмите нули многоугольника управления Dc как ваше первое предположение для нулей Dc. Для этого необходимо демонтировать сплайн Dc.

[knots,coefs,np,kp] = fnbrk(Dc,'knots','coefs','n','order');

Многоугольник управления имеет вершины (tstar(i), coefs(i)), с tstar средние значения узла для сплайна, обеспеченного aveknt:

tstar = aveknt(knots,kp);

Вот нули получившегося многоугольника управления Dc:

npp = (1:np-1); 
guess = tstar(npp) -coefs(npp).*(diff(tstar)./diff(coefs));

Это уже обеспечивает очень хорошее первое предположение для фактических нулей.

Совершенствуйте эту оценку для нулей Dc двумя шагами метода секущей, беря tau и получившийся guess как ваши первые приближения. Во-первых, оцените Dc в обоих наборах:

sites = tau(ones(4,1),2:n-1); 
sites(1,:) = guess; 
values = zeros(4,n-2); 
values(1:2,:) = reshape(fnval(Dc,sites(1:2,:)),2,n-2);

Теперь приезжайте два шага метода секущей. Вы принимаете меры против деления на нуль путем установки различия в значении функции для 1 в случае, если это - нуль. Поскольку Dc является строго монотонным около разыскиваемых сайтов, это безопасно:

for j=2:3 
  rows = [j,j-1];Dcd=diff(values(rows,:));
  Dcd(find(Dcd==0)) = 1; 
  sites(j+1,:) = sites(j,:) ... 
           -values(j,:).*(diff(sites(rows,:))./Dcd); 
  values(j+1,:) = fnval(Dc,sites(j+1,:)); 
end

Проверка

max(abs(values.')) 
  ans = 4.1176 5.7789 0.4644 0.1178

показывает улучшение.

Теперь возьмите эти сайты в качестве своего нового tau,

tau = [tau(1) sites(4,:) tau(n)];

и проверяйте экстремальные значения своего текущего приближения там:

extremes = abs(fnval(c, tau));

Различие

max(extremes)-min(extremes)
  ans = 0.6905

оценка того, как далеко вы от общего выравнивания.

Создайте новый сплайн, соответствующий новому выбору tau и постройте его сверху старого:

c = spapi(t,tau,b); 
sites = sort([tau (0:100)*(t(n+1)-t(k))/100]); 
values = fnval(c,sites); 
hold on, plot(sites,values)

Следующий код включает сетку и строит местоположения экстремального значения.

grid on
plot( tau(2:end-1), zeros( 1, np-1 ), 'o' )
hold off
legend( 'Initial Guess', 'Current Guess', 'Extreme Locations',...
 'location', 'NorthEastOutside' );

Следующее является получившейся фигурой (легенда, не показанная).

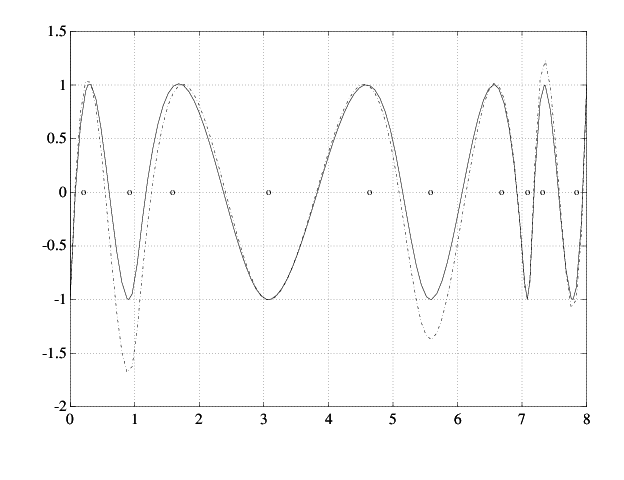
Если это не достаточно близко, каждый просто повторяет цикл. В данном примере следующая итерация уже производит C для графической точности.