В приложении Curve Fitting выберите Interpolant из списка типов модели.
Interpolant подходящая категория соответствует кривой интерполяции или поверхности, которая проходит через каждую точку данных. Для поверхностей тип подгонки Interpolant использует MATLAB® scatteredInterpolant функция для линейных и самых близких методов, MATLAB griddata функция для кубических и бигармонических методов, и tpaps функция для интерполяции сплайна тонкой пластины.
Настройки показывают здесь.
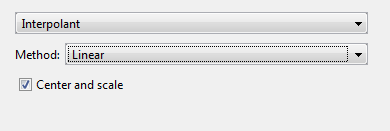
Можно задать установку Method: Nearest neighbor, Linear, Cubic, Shape-preserving (PCHIP) (для кривых), Biharmonic (v4) (для поверхностей) или Thin-plate spline (для поверхностей). Для получения дополнительной информации займитесь Методами интерполяции.
Совет
Если вы соответствуете поверхности, и ваши входные переменные имеют различные шкалы, включают и выключают опцию Center and scale, чтобы видеть различие в поверхностной подгонке. Нормализация входных параметров может строго влиять на результаты основанного на треугольнике (т.е. кусочный Linear и Cubic интерполяция) и Nearest neighbor поверхностные методы интерполяции.
Для поверхностей попробуйте сплайны тонкой пластины, когда вы потребуете и сглаженной поверхностной интерполяции и хороших свойств экстраполяции.
fit ФункцияВ этом примере показано, как использовать fit функция, чтобы подбирать линейные interpolant модели к данным.
Interpolant подходящие методы
Задайте interpolant метод модели при вызывании подходящей функции с помощью одной из опций, обрисованных в общих чертах в Именах модели Interpolant. Ни один из interpolant методов не имеет дополнительных подходящих опциональных параметров.
Подбирайте линейную модель Interpolant
Загрузите данные и подбирайте линейную interpolant модель с помощью 'linearinterp' опция.
load census f = fit(cdate,pop,'linearinterp'); plot(f,cdate,pop);

Сравните линейные модели Interpolant
Загрузите данные и создайте и самого близкого соседа и pchip interpolant подгонки с помощью 'nearestinterp' и 'pchip' опции.
load carbon12alpha f1 = fit(angle,counts,'nearestinterp'); f2 = fit(angle,counts,'pchip');
Сравните кривые по экспериментальным точкам f1 и f2 на графике.
p1 = plot(f1,angle,counts); xlim([min(angle),max(angle)]) hold on p2 = plot(f2,'b'); hold off legend([p1;p2],'Counts per Angle','Nearest Neighbor','pchip',... 'Location','northwest')

Для альтернативы 'cubicinterp' или 'pchipinterp', можно использовать другие функции сплайна, которые дают вам больший контроль над тем, что вы создаете. Займитесь Сплайнами в Curve Fitting Toolbox.