Основы нечеткой логики

Обзор

Точка нечеткой логики должна сопоставить входное пространство с выходным пробелом и первичный механизм для того, чтобы сделать, это - список того, если затем операторы вызвали правила. Все правила оценены параллельно, и порядок правил неважен. Сами правила полезны, потому что они обращаются к переменным и прилагательным, которые описывают те переменные. Прежде чем можно будет создать систему, которая интерпретирует правила, необходимо задать все термины, которые вы планируете на использовании и прилагательных, которые описывают их. Чтобы сказать, что вода является горячей, необходимо задать область значений, в которой температура воды, как могут ожидать, будет варьироваться, а также что вы подразумеваете под горячим словом.

В общем случае нечеткий вывод является методом, который интерпретирует значения во входном векторе и, на основе некоторого ряда правил, присваивает значения выходному вектору.

Эта тема проводит вас по процессу нечеткой логики, постепенному путем обеспечения введения в теорию и практику нечеткой логики.

Нечеткие множества

Нечеткая логика запускается с концепции нечеткого множества. fuzzy set является набором без хрустящего картофеля, ясно заданного контура. Это может содержать элементы только с частичной степенью членства.

Чтобы изучить, каково нечеткое множество, сначала рассмотрите определение классического набора. Классический набор является контейнером, который полностью включает или полностью исключает любой данный элемент. Например, набор дней недели бесспорно включает в понедельник, в четверг, и в субботу. Это столь же бесспорно исключает масло, свободу и спинные плавники, и так далее.

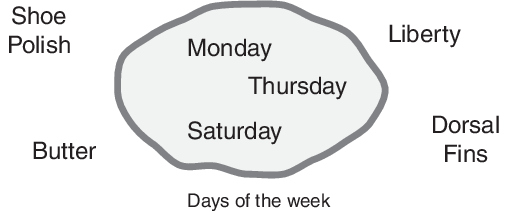
A classical set containing days of the week in the center surrounded by elements that are not days of the week

Этот тип набора называется классическим набором, потому что это было вокруг в течение долгого времени. Именно Аристотель сначала сформулировал Закон исключенного третьего, который говорит X, должен или быть в наборе A или в наборе не-A. Другая версия этого закона:

Из любого предмета одна вещь должна или утверждаться или отклоняться.

Вновь заявить об этом законе с аннотациями: "Любого предмета (говорят в понедельник), одна вещь (день недели) должна или утверждаться или отклоняться (я утверждаю, в тот понедельник день недели)". Этот закон требует, чтобы противоположности, эти две категории A и не-A, были должны между ними содержать целую вселенную. Все попадает или в одну группу или в другой. Нет никакой вещи, которая является и днем недели и не днем недели.

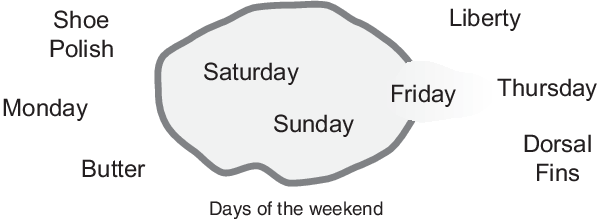
Теперь рассмотрите набор дней, включив выходные. Следующая схема пытается классифицировать дни выходных дней.

Большинство согласилось бы в ту субботу, и воскресенье принадлежат набора выходных дней, но что относительно пятницы? Похоже на часть выходных, но так или иначе кажется, что это должно быть технически исключено. Поэтому пятница "сохраняет нейтралитет". Классические наборы не терпят этот вид классификации. Или что-то находится в наборе, или это вне набора. Человеческий опыт показывает что-то другое, однако, сохранение нейтралитет является частью жизни.

The weekend set, which contains Saturday and Sunday, in the center surrounded by elements that are not weekend days. Friday straddles the edge of the weekend set.

Конечно, отдельное восприятие и культурное наследие должны быть учтены, когда вы задаете то, что составляет выходные. Даже словарь неточен, задавая выходные как период с ночи пятницы или субботы к утру понедельника. Вы вводите область, где с острым краем, да - никакая логика не прекращает быть полезной. Нечеткое обоснование становится ценным точно, когда вы работаете с тем, как люди действительно чувствуют выходные концепции в противоположность бесхитростной классификации, полезной для бухгалтерских целей только. Больше, чем что-либо еще, следующий оператор закладывает основы нечеткой логике.

В нечеткой логике истина любого оператора становится вопросом степени.

Любой оператор может быть нечетким. Главным преимуществом, которое предлагает нечеткое обоснование, является способность ответить на вопрос, требующий ответа "да - нет" с не вполне да или никакой ответ. Люди делают такого рода вещь все время (думайте, как редко вы получаете прямой ответ на на вид простой вопрос), но это - довольно новый прием для компьютеров.

Как это работает? Обоснование в нечеткой логике является только вопросом обобщения знакомого да - никакая (булева) логика. Если вы даете верный численное значение 1 и ложь численное значение 0, это значение указывает, что нечеткая логика также разрешает промежуточные значения как 0,2 и 0.7453. Например:

Q: Действительно ли суббота является днем выходных дней?

A: 1 (да, или верный)

Q: Действительно ли вторник является днем выходных дней?

A: 0 (не, или ложь)

Q: Действительно ли пятница является днем выходных дней?

A: 0.8 (по большей части да, но не полностью)

Q: Действительно ли воскресенье является днем выходных дней?

A: 0.95 (да, но не совсем целая суббота).

График слева показывает значения истинности для мыса выходных дней, если вы обеспечены, чтобы ответить абсолютом да или никакой ответ. Справа график, который показывает значение истинности для мыса выходных дней, если вам разрешают ответить нечеткими промежуточными значениями.

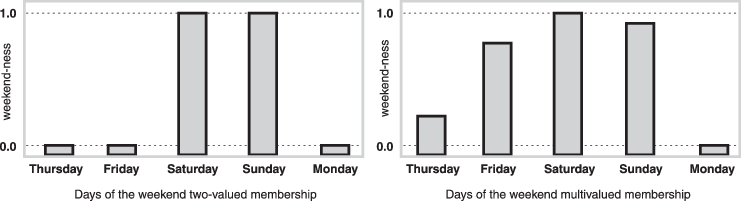
In the left plot, Thursday and Friday have zero weekend membership. In the right plot, these days have nonzero memberships less than 1, with Friday greater than Thursday.

Технически, представление справа от области многозначной логики (или многовалентная логика). Если вы задаете вопрос, "X член набора A?" ответ может быть да, нет, или любое из тысячи промежуточных промежуточных значений. Таким образом, X может иметь частичное членство в A. Многозначная логика выдерживает на прямом контрасте по отношению к более знакомой концепции двузначных (или дуальный да - нет) логику.

Чтобы возвратиться к примеру, теперь считайте непрерывный график временной зависимости шкалы мыса выходных дней показанным в следующих графиках.

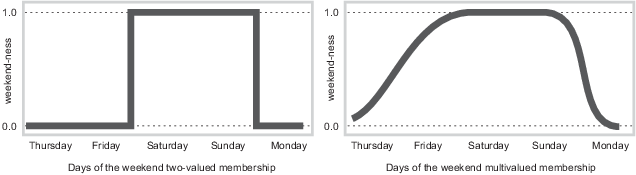
In the left plot, the membership plot has sharp transitions on either side of Saturday and Sunday. In the right plot, the transition from weekend to nonweekend is smooth.

Путем создания графика непрерывным, вы задаете степень, которой любой данный момент принадлежит в выходные, а не целый день. В графике слева, заметьте в полночь в пятницу, когда секундная стрелка проносится мимо 12, значение истинности мыса выходных дней переходит с перерывами с 0 до 1. Это - один способ задать выходные, и в то время как это может быть полезно для бухгалтера, это не может действительно соединиться с вашим собственным реальным опытом мыса выходных дней.

График справа показывает гладко различную кривую, которая составляет то, что вся пятница, и, до маленькой степени, частей четверга, разделяет качество мыса выходных дней и таким образом заслуживает частичного членства в нечетком множестве моментов выходных дней. Кривая, которая задает мыс выходных дней любого момента вовремя, является функцией, которая сопоставляет входное пространство (время недели) к выходному пробелу (мыс выходных дней). А именно, это известно как функцию принадлежности. Смотрите Функции принадлежности для более детального обсуждения.

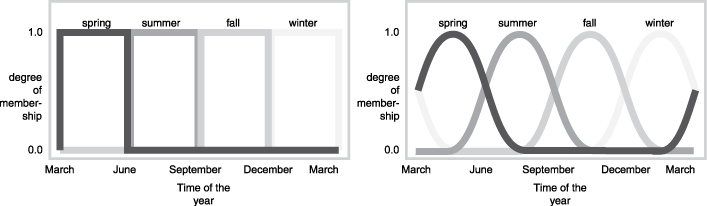
Как другой пример нечетких множеств, рассмотрите вопрос сезонов. Какой сезон - он прямо сейчас? В северном полушарии лето официально начинается в точный момент в орбите земли, когда Северный полюс указан наиболее непосредственно к солнцу. Это происходит точно один раз в год в конце июня. Используя астрономические определения в течение сезона, вы получаете резкие контуры как показано слева на рисунке, который следует. Но что вы испытываете, когда сезоны варьируются более или менее постоянно как показано справа в следующем рисунке (в умеренных климатах северного полушария).

The left plot shows crisp boundaries between seasons. The right plot shows smooth overlapping season boundaries.

Функции принадлежности

Функция принадлежности (MF) является кривой, которая задает соответствие каждой входной переменной (элементу входного множества) значение степени выраженности, лежащее между 0 и 1. Входные переменные иногда называют элементами универсального множества.

Одним из обычно используемых примеров нечеткого множества является группа высоких людей. В этом случае вселенная беседы является всеми потенциальными высотами, скажите от трех футов до девяти футов, и высокое слово соответствовало бы кривой, которая задает степень, до которой любой человек высок. Если группе высоких людей дают четко определенный (четкий) контур классического набора, вы можете сказать, что все люди, более высокие, чем шесть футов, официально рассматриваются высокими. Однако такое различие явно абсурдно. Это может быть целесообразно считать набор всех вещественных чисел больше, чем шесть, потому что числа принадлежат на абстрактной плоскости, но когда мы хотим говорить о настоящих людях, неблагоразумно вызвать одного короткого человека и другой высокий, когда они отличаются по высоте шириной волоска.

You must be taller than this line to be considered tall. The one person over the line in a group of people is happy with this classification.

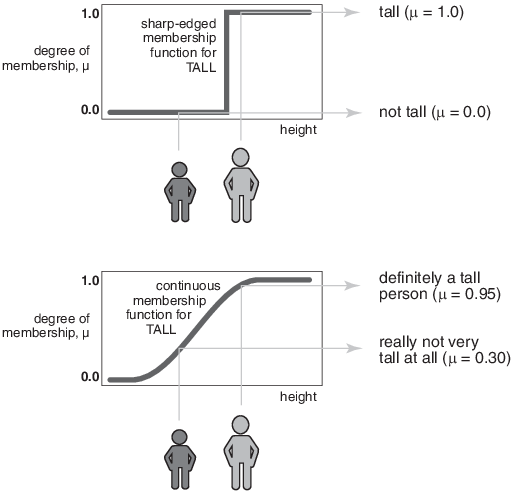
Если вид различия, показанного ранее, неосуществим, то, что правильный путь состоит в том, чтобы задать группу высоких людей? Как с графиком дней выходных дней, следующее фигуры показывает гладко различную кривую что передачи от не - высокий к высокому. Выходная ось является номером, известным как значение членства между 0 и 1. Кривая известна как функцию принадлежности и часто дается обозначение µ. Например, следующий рисунок показывает и хрустящий картофель и сглаженные высокие функции принадлежности. В главном графике эти два человека классифицируются или как совершенно высокие или как полностью не - высокий. В нижнем графике плавный переход допускает различные степени высоты. Оба человека высоки до некоторой степени, но каждый значительно менее высок, чем другой. Более высокий человек, с членством в высоте 0,95 является определенно высоким человеком, но человек с членством в высоте 0,3 не очень высок.

In the top plot, a crisp membership function shows a sharp transition from not-tall to tall. In the bottom plot, a smooth transition allows for degrees of tallness.

Субъективные интерпретации и соответствующие модули встроены прямо в нечеткие множества. Если вы говорите, что "Она высока", высокая функция принадлежности должна уже учесть, обращаетесь ли вы к шестилетнему или выращенной женщине. Точно так же модули включены в кривую. Конечно, не имеет никакого смысла говорить, что "Действительно ли она высока в дюймах или в метрах?"

Функции принадлежности в программном обеспечении Fuzzy Logic Toolbox

Единственное условие, которому должна действительно удовлетворить функция принадлежности, состоит в том, что она должна находиться в интервале между 0 и 1. Сама функция может быть произвольной кривой, форму которой мы можем задать как функция, которая подходит нам с точки зрения простоты, удобства, скорости и КПД.

Классический набор может быть описан как

$A = {x | x > 6}$

Нечеткое множество является расширением классического набора. Если X является вселенной беседы, и ее элементы обозначаются x, то нечеткое множество A в X задано в виде набора упорядоченных пар.

$A {x, μ_{A} (x) | x \in X}$

A = {x, _µA (x) | x ∈ X}

_µA (x) называется функцией принадлежности (или MF) x в A. Функция принадлежности сопоставляет каждый элемент X к значению членства между 0 и 1.

Тулбокс включает 11 встроенных типов функции принадлежности. Эти 11 функций, в свою очередь, создаются из нескольких основных функций:

Кусочные линейные функции
Функция распределения Гаусса
Сигмоидальная кривая
Кривые квадратичного и кубического полинома

Для получения дальнейшей информации на любой из функций принадлежности, упомянутых затем, смотрите соответствующую страницу с описанием.

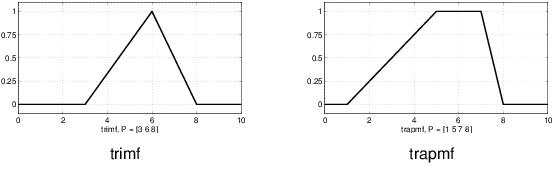
Самые простые функции принадлежности формируются с помощью прямых линий. Из них самой простой является треугольная функция принадлежности, и она имеет имя функции trimf. Эта функция является не чем иным как набором трех точек, формирующих треугольник. Трапециевидная функция принадлежности, trapmf, имеет стрижку под ежика и действительно только усеченная треугольная кривая. Эти функции принадлежности прямой линии имеют преимущество простоты.

Sample triangular and trapezoidal membership functions on the left and right, respectively

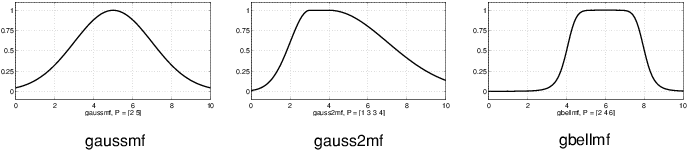
Две функции принадлежности основаны на кривой Распределения Гаусса: простая Кривая Гаусса и двухсторонний составной объект двух различных Кривых Гаусса. Двумя функциями является gaussmf и gauss2mf.

Обобщенная функция принадлежности звонка задана тремя параметрами и имеет имя функции gbellmf. Функция принадлежности звонка имеет еще один параметр, чем Гауссова функция принадлежности, таким образом, это может приблизиться к ненечеткому множеству, если свободный параметр настраивается. Из-за их гладкости и краткого обозначения, Гауссова и функции принадлежности звонка, популярные методы для определения нечетких множеств. Обе из этих кривых имеют преимущество явления гладкого и быть ненулевым во всех точках.

From left to right, sample Gaussian, two-sided Gaussian, and generalized bell membership functions

Несмотря на то, что Гауссовы функции принадлежности и функции принадлежности звонка достигают гладкости, они не могут задать асимметричные функции принадлежности, которые важны в определенных приложениях. Затем вы задаете сигмовидную функцию принадлежности, которая является любой открыта левый или правый. Асимметричный и закрытый (т.е. не открытые налево или направо) функции принадлежности могут быть синтезированы с помощью двух сигмовидных функций, таким образом, в дополнение к основному sigmf, у вас также есть различие между двумя сигмовидными функциями, dsigmf, и продукт двух сигмовидных функций psigmf.

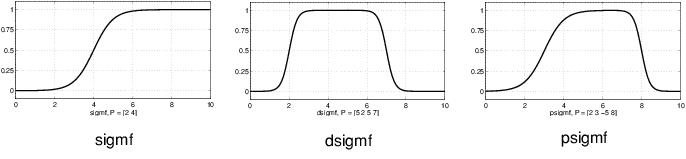
From left to right, sample sigmoidal, difference of sigmoids, and product of sigmoids membership functions

Основанные на полиноме кривые составляют несколько из функций принадлежности в тулбоксе. Три связанных функции принадлежности являются Z, S, andPi кривые, все названные из-за их формы. Функциональный zmf асимметричная полиномиальная кривая, открытая налево, smf функция зеркального отображения, которая открывается направо, и pimf нуль на обоих экстремальных значениях с повышением в середине.

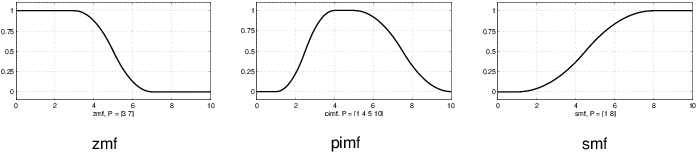
From left to right, sample Z, pi, and S membership function

Существует очень широкий выбор, чтобы выбрать из того, когда вы выбираете функцию принадлежности. Можно также создать собственные функции принадлежности с тулбоксом. Однако, если список на основе расширенных функций принадлежности кажется слишком сложным, только помните, что вы могли, вероятно, ладить очень хорошо со всего одним или двумя типами функций принадлежности, например, функции трапецоида и треугольник. Выбор широк для тех, кто хочет исследовать возможности, но расширяемые функции принадлежности не необходимы для хороших нечетких систем вывода. Наконец, помните, что больше деталей доступно на всех этих функциях в ссылочном разделе.

Сводные данные функций принадлежности

Нечеткие множества описывают неопределенные концепции (например, быстрый бегун, жаркая погода, дни выходных дней).
Нечеткое множество допускает возможность частичного членства в нем. (например, пятница является видом дня выходных дней, погода является довольно горячей).
Степень объект принадлежит нечеткому множеству, обозначается значением членства между 0 и 1 (например, пятница является днем выходных дней до степени 0.8).
Функция принадлежности, сопоставленная с данным нечетким множеством, сопоставляет входное значение со своим соответствующим значением членства.

Логические операции

Теперь, когда вы изучаете нечеткий вывод, вам нужно, чтобы видеть, как нечеткий вывод соединяется с логическими операциями.

Самой важной вещью понять о нечетком логическом обосновании является то, что это - надмножество стандартной Булевой логики. Другими словами, если вы сохраняете нечеткие значения в их экстремальных значениях 1 (абсолютно верными), и 0 (абсолютно ложных), стандартных логических операций будут содержать. Как пример, рассмотрите следующие стандартные таблицы истинности.

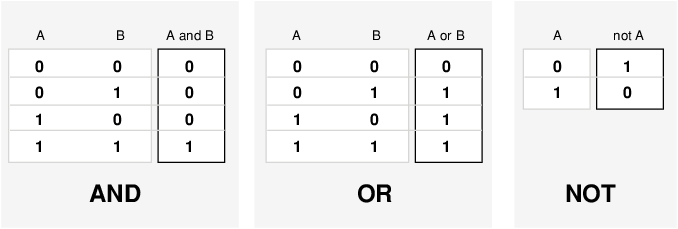
The and operation is 1 when both inputs are 1. The or operation is one when either input is 1. The not operation is 1 when the input is zero.

По этой причине, в нечеткой логике истина какого-либо оператора является вопросом степени, эти таблицы истинности могут быть изменены? Входные значения могут быть вещественными числами между 0 и 1. Какая функция сохраняет результаты таблицы истинности AND (например), и также расширьте ко всем вещественным числам между 0 и 1?

Один ответ является операцией min. Таким образом, разрешите оператор A AND B, где A и B ограничиваются областью значений (0,1), при помощи функционального min (A, B). Используя то же обоснование, можно заменить операцию OR на макс. функцию, так, чтобы OR B стал эквивалентным макс. (A, B). Наконец, операция NOT A становится эквивалентной операции $1 - A$ . Предыдущая таблица истинности абсолютно неизменна этой заменой.

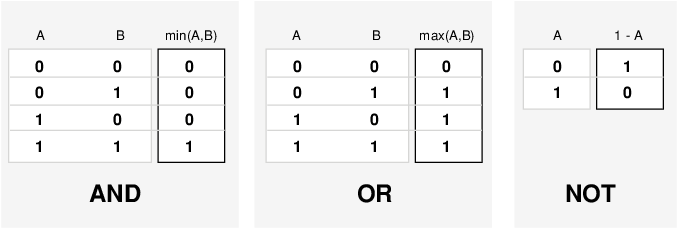
The minimum, maximum, and not fuzzy logic operators produce the same truth tables for crisp input values as Boolean logic does for and, or, and not operations, respectively.

Кроме того, потому что существует функция позади таблицы истинности, а не только самой таблицы истинности, можно теперь рассмотреть значения кроме 1 и 0.

Следующая фигура использует график, чтобы показать ту же информацию. В этом рисунке таблица истинности преобразована в график двух нечетких множеств, примененных вместе, чтобы создать одно нечеткое множество. Верхняя часть фигуры отображает графики, соответствующие предыдущим двузначным таблицам истинности, в то время как более низкая часть фигуры отображается, как операции перерабатывают постоянно различную область значений значений истинности A и B согласно нечетким операциям, которые вы задали.

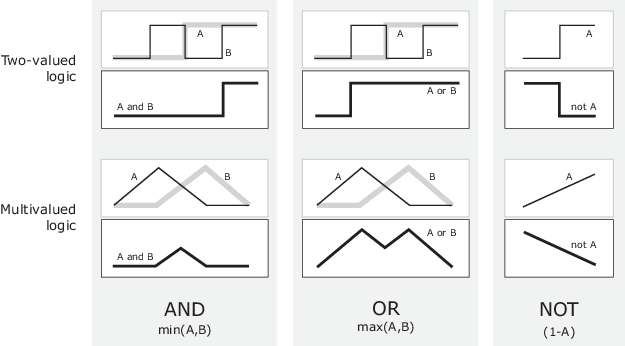
From left to right, AND , OR, and NOT operations in both two-valued and multivalued logic

Учитывая эти три функции, можно разрешить любую конструкцию с помощью нечетких множеств и нечеткой логической операции AND, OR, и НЕТ.

Дополнительные нечеткие операторы

В этом случае вы задали только одно конкретное соответствие между двузначными и многозначными логическими операциями для AND, OR, и НЕТ. Это соответствие ни в коем случае не уникально.

В более общих чертах вы задаете то, что известно как нечеткое пересечение или соединение (AND), нечеткое объединение или дизъюнкция (OR) и нечеткое дополнение (НЕТ). Классические операторы для этих функций: AND = min, OR = макс., и НЕ = аддитивное дополнение. Как правило, большинство приложений нечеткой логики использует эти операции и оставляет его в этом. В общем случае однако эти функции произвольны до удивительной степени. Программное обеспечение Fuzzy Logic Toolbox™ использует классический оператор для нечеткого дополнения как показано на предыдущем рисунке, но также и позволяет вам настроить операции И и операции ИЛИ.

Пересечение двух нечетких множеств A и B задано в целом двоичным файлом, сопоставляющим T, который агрегировал две функции принадлежности можно следующим образом:

$μ_{A \cap B} (x) = T (μ_{A} (x), μ_{B} (x))$

Например, бинарный оператор T может представлять умножение _µA (x) и _µB (x). Эти нечеткие операторы пересечения, которые обычно упоминаются как T - норма (Треугольная норма) операторы, удовлетворяют следующие основные требования:

T - оператор нормы является двоичным файлом, сопоставляющим T (..) со следующими свойствами:

Контур $T (0, 0) = 0, T (a, 1) = T (1, a) = a$
Монотонность — $T (a, b) \leq T (c, d)$ если $a \leq c$ и $b \leq d$
Коммутативность — $T (a, b) = T (b, a)$
Ассоциативность — $T (a, T (b, c)) = T (T (a, b), c)$

Первое требование налагает правильное обобщение к четким наборам. Второе требование подразумевает, что уменьшение в значениях членства в A или B не может произвести увеличение значения членства в пересечении B. Третье требование указывает, что оператор равнодушен к порядку нечетких множеств, которые будут объединены. Наконец, четвертое требование позволяет нам брать пересечение любого количества наборов в любом порядке попарных группировок.

Как нечеткое пересечение, нечеткий оператор объединения задан в целом двоичным файлом, сопоставляющим S:

$μ_{A \cup B} (x) = S (μ_{A} (x), μ_{B} (x))$

Например, бинарный оператор S может представлять сложение _µA (x) и _µB (x). Эти нечеткие операторы объединения, которые часто упоминаются как T-conorm (или S - норма) операторы, должны удовлетворить следующим основным требованиям:

T-conorm (или S - норма) оператор является двоичным файлом, сопоставляющим S (..) со следующими свойствами:

Контур $S (1, 1) = 1, S (a, 0) = S (0, a) = a$
Монотонность — $S (a, b) \leq S (c, d)$ если $a \leq c$ и $b \leq d$
Коммутативность — $S (a, b) = S (b, a)$
Ассоциативность — $S (a, S (b, c)) = S (S (a, b), c)$

Несколько параметрировали T - нормы и двойной T-conorms были предложены в прошлом, такие как те Yager [11], Дюбуа и Прэйд [1], Schweizer и Sklar [8] и Sugeno [9]. Каждый из них обеспечивает способ изменять усиление на функции так, чтобы это могло быть очень строгим или очень разрешающим.

Если затем правила

Нечеткие множества и нечеткие операторы являются предметами и глаголами нечеткой логики. Они, если затем операторы правила используются, чтобы сформулировать условные операторы, которые включают нечеткую логику.

Сингл, нечеткий, если затем правило принимает форму

Если x является A, то y является B

где A и B являются лингвистическими значениями, заданными нечеткими множествами на областях значений (вселенные беседы) X и Y, соответственно. Если-часть правила "x", называется антецедентом или предпосылкой, в то время как тогдашняя часть правила "y является B", называется следствием или заключением. Пример такого правила может быть

Если сервис хорош, то чаевые средние

Хорошая концепция представлена как номер между 0 и 1, и таким образом, антецедент является интерпретацией, которая возвращает один номер между 0 и 1. С другой стороны среднее значение представлено как нечеткое множество, и таким образом, следствие является присвоением, которое присваивает целое нечеткое множество B выходной переменной y. В, если затем правило, слово, привыкает двумя совершенно различными способами в зависимости от того, появляется ли это в антецеденте или следствии. В MATLAB^® термины, это использование является различием между реляционным тестовым использованием "==" и переменным присвоением с помощью "=" символ. Менее запутывающий способ записать правило был бы

Если сервис == хороший, то снабдите подсказкой = среднее значение

В общем случае вход к, если затем правило является текущим значением для входной переменной (в этом случае, сервис) и выход, является целым нечетким множеством (в этом случае, среднее значение). Этот набор позже будет defuzzified, присваивая одно значение выходу. Концепция дефаззификации описана в следующем разделе.

Интерпретация, если затем правило включает два шага:

Оценка антецедента — Fuzzifying входные параметры и применение любых необходимых нечетких операторов.
Приложение результата к следствию.

Второй шаг известен как значение. Для, если затем правило, антецедент, p, подразумевает следствие, q. В бинарной логике, если p верен, то q также верен (p → q). В нечеткой логике, если p верен для некоторой степени членства, то q также верен для той же степени (0.5p → 0.5q). В обоих случаях, если p является ложным, то значение q является неопределенным.

Антецедент правила может иметь несколько частей.

Если небо является серым, и ветер силен, и барометр падает, то...

В этом случае все части антецедента вычислены одновременно и разрешены к одному номеру с помощью логических операторов, описанных в предыдущем разделе. Следствие правила может также иметь несколько частей.

Если температура является холодной, то клапан горячей воды открыт, и клапан холодной воды закрывается

В этом случае все следствия затронуты одинаково результатом антецедента. Как следствие затронуто антецедентом? Следствие задает нечеткое множество быть присвоенным выходу. Функция значения затем изменяет то нечеткое множество до степени, заданной антецедентом. Наиболее распространенные способы изменить выходное нечеткое множество являются усечением с помощью min функция (где нечеткое множество является усеченным как показано в следующем рисунке), или масштабирующий использование prod функция (где выходное нечеткое множество раздавлено). Оба поддерживаются тулбоксом, но вы используете усечение для примеров в этом разделе.

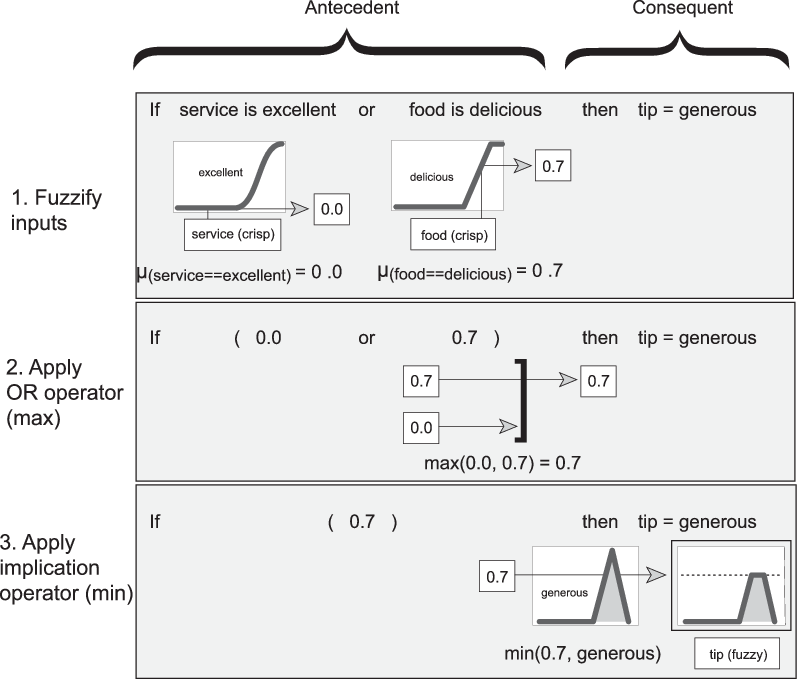
Fuzzy rule evaluation steps from top to bottom: Fuzzify inputs, apply logical operator to fuzzified inputs, apply implication operator to the antecedent outputs

Сводные данные если затем правила

Интерпретация, если затем правила трехчастный процесс. Этот процесс объяснен подробно в следующем разделе:

Входные параметры Fuzzify: Разрешите все нечеткие операторы в антецеденте до степени членства между 0 и 1. Если существует только одна часть к антецеденту, то это - степень поддержки правила.
Примените нечеткий оператор к нескольким антецедентам части: Если существует несколько частей к антецеденту, применяют операторы нечеткой логики и разрешают антецедент к одному номеру между 0 и 1. Это - степень поддержки правила.
Примените метод значения: Используйте степень поддержки целого правила сформировать выходное нечеткое множество. Следствие нечеткого правила присваивает целое нечеткое множество выходу. Это нечеткое множество представлено функцией принадлежности, которая выбрана, чтобы указать на качества следствия. Если антецедент только частично верен, (i.e., присвоен значение 1), затем выходное нечеткое множество является усеченным согласно методу значения.

В общем случае одно единственное правило не является эффективным. Необходимы два или больше правила, которые могут вопроизвести друг от друга. Выход каждого правила является нечетким множеством. Выходные нечеткие множества для каждого правила затем агрегированы в одно выходное нечеткое множество. Наконец получившийся набор является defuzzified, или разрешенный к одному номеру. Нечеткие Системы сборки Используя Fuzzy Logic Designer показывают, как целый процесс работает с начала до конца на конкретный тип нечеткой системы вывода, названной типом Mamdani.

Ссылки

[1] Дюбуа, Дидье и Анри М. Прад. Нечеткие множества и Системы: Теория и Приложения. Математика в Науке и Разработке, v. 144. Нью-Йорк: Academic Press, 1980.

[2] Кауфманн, A. и Мадан М. Гупта. Введение в Нечеткую Арифметику: Теория и Приложения. Электрический ван Нострэнд Райнхольд / Информатика и Технический Ряд. Нью-Йорк, Нью-Йорк: Van Nostrand Reinhold Co, 1985.

[3] Ли, C.C. ‘Нечеткая логика в Системах управления: Контроллер Нечеткой логики. I. Транзакции IEEE в Системах, Человеке и Кибернетике 20, № 2 (апрель 1990): 404–18. https://doi.org/10.1109/21.52551.

[4] Ли, C.C. ‘Нечеткая логика в Системах управления: Контроллер Нечеткой логики. II’. Транзакции IEEE в Системах, Человеке и Кибернетике 20, № 2 (апрель 1990): 419–35. https://doi.org/10.1109/21.52552.

[5] Mamdani, E.H., и С. Ассилиэн. ‘Эксперимент в Лингвистическом Синтезе с Контроллером Нечеткой логики’. Международный журнал Человеко-машинных Исследований 7, № 1 (январь 1975): 1–13. https://doi.org/10.1016/S0020-7373 (75) 80002-2.

[6] Mamdani, E.H. ‘Усовершенствования в Лингвистическом Синтезе Нечетких Контроллеров’. Международный журнал Человеко-машинных Исследований 8, № 6 (ноябрь 1976): 669–78. https://doi.org/10.1016/S0020-7373 (76) 80028-4.

[7] Mamdani, E.H. ‘Приложение Нечеткой логики, чтобы Аппроксимировать Обоснование Используя Лингвистический Синтез’. Транзакции IEEE на Компьютерах C–26, № 12 (декабрь 1977): 1182–91. https://doi.org/10.1109/TC.1977.1674779.

[8] Schweizer, B. и А. Склэр, 'Ассоциативные функции и абстрактные полугруппы. Publ. Математика. Дебрецен 10 (1963): 69–81.

[9] Sugeno, M., "Нечеткие меры и нечеткие интегралы: обзор", (М.М. Гупта, Г. Н. Сэридис, и Б.Р. Гэйнс, редакторы) Нечеткие Автоматы и Процессы принятия решений, стр 89-102, Северная Голландия, Нью-Йорк, 1977.

[10] Sugeno, Michio, Промышленное применение редактора Нечеткого Управления. Амстердам  ; Нью-Йорк  : Нью-Йорк, Нью-Йорк, U.S.A: северная Голландия  ; Единственные дистрибьюторы для U.S.A. и Канада, паб Elsevier Science. Ко, 1985.

[11] Yager, Рональд Р. ‘На Общем Классе Нечетких Соединительных слов’. Нечеткие множества и Системы 4, № 3 (ноябрь 1980): 235–42. https://doi.org/10.1016/0165-0114 (80) 90013-5.

[12] Yager, Рональд Р. и Димитар П. Филев. ‘Генерация Нечетких Правил Горной Кластеризацией’. Журнал Интеллектуальных и Нечетких Систем 2, № 3 (1994): 209–19. https://doi.org/10.3233/IFS-1994-2301.

[13] Zadeh, лос-анджелесские 'Нечеткие множества'. Информация и Управление 8, № 3 (июнь 1965): 338–53. https://doi.org/10.1016/S0019-9958 (65) 90241-X.

[14] Zadeh, Лотфи А. ‘Схема Нового Подхода к Анализу Сложных систем и Процессам принятия решений’. Транзакции IEEE в Системах, Человеке и Кибернетике SMC-3, № 1 (1973): 28–44. https://doi.org/10.1109/TSMC.1973.5408575.

[15] Zadeh, Лос-Анджелес 'Концепция лингвистической переменной и ее приложения, чтобы аппроксимировать обоснование. Я '.Information Науки 8, № 3 (1975): 199–249. https://doi.org/10.1016/0020-0255 (75) 90036-5

[16] Zadeh, Лос-Анджелес 'Концепция лингвистической переменной и ее приложения, чтобы аппроксимировать обоснование. II'. Информатика 8, № 4 (1975): 301–357. https://doi.org/10.1016/0020-0255 (75) 90046-8

[17] Zadeh, Лос-Анджелес 'Концепция лингвистической переменной и ее приложения, чтобы аппроксимировать обоснование. III'. Информатика 9, № 1 (1975):43-80. https://doi.org/10.1016/0020-0255 (75) 90017-1

[18] Zadeh, лос-анджелесская 'Нечеткая логика'. Компьютер 21, № 4 (апрель 1988): 83–93. https://doi.org/10.1109/2.53.

[19] Zadeh, лос-анджелесское ‘Представление знаний в Нечеткой логике’. Транзакции IEEE на Разработке Знания и Данных 1, № 1 (март 1989): 89–100. https://doi.org/10.1109/69.43406.

Документация