Следующая схема подводит итог, как генетический алгоритм работает:
Алгоритм начинается путем создания случайной начальной генеральной совокупности.
Алгоритм затем создает последовательность новых популяций. На каждом шаге алгоритм использует индивидуумов в текущем поколении, чтобы создать следующее население. Чтобы создать новое население, алгоритм выполняет следующие шаги:
Считает каждый член текущей популяции путем вычисления ее значения соответствия. Эти значения называются необработанными баллами фитнеса.
Масштабирует необработанные баллы фитнеса, чтобы преобразовать их в более применимую область значений значений. Эти масштабированные значения называются значениями ожидания.
Выбирает члены, названные родительскими элементами, на основе их ожидания.
Некоторые индивидуумы в текущем населении, которые имеют более низкий фитнес, выбраны в качестве элиты. Эти элитные индивидуумы передаются следующему населению.
Производит дочерние элементы из родительских элементов. Дочерние элементы производятся или путем внесения случайных изменений в единый объект-родитель — мутацию — или путем объединения векторных записей пары родительских элементов — перекрестное соединение.
Заменяет текущее население на дочерние элементы, чтобы сформировать следующее поколение.
Алгоритм останавливается, когда достигается один из критериев остановки. Смотрите Останавливающиеся Условия для Алгоритма.
Алгоритм делает измененные шаги для линейных и целочисленных ограничений. Смотрите Целочисленные и Линейные Ограничения.
Алгоритм далее изменяется для нелинейных ограничений. Смотрите Нелинейные Ограничительные Алгоритмы решателя.
Алгоритм начинается путем создания случайной начальной генеральной совокупности как показано в следующем рисунке.
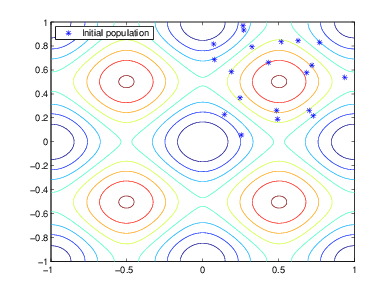
В этом примере начальная генеральная совокупность содержит 20 индивидуумы. Обратите внимание на то, что все индивидуумы в начальной генеральной совокупности лежат в верхнем правом квадранте изображения, то есть, их координаты находятся между 0 и 1. В данном примере InitialPopulationRange опцией является [0;1].
Если вы знаете приблизительно, где минимальная точка для функции находится, необходимо установить InitialPopulationRange так, чтобы точка нашлась около середины той области значений. Например, если вы полагаете, что минимальной точкой для функции Рэстриджина является около точки [0 0], вы могли установить InitialPopulationRange быть [-1;1]. Однако, когда этот пример показывает, генетический алгоритм может найти минимум даже с меньше, чем оптимальный выбор для InitialPopulationRange.
На каждом шаге генетический алгоритм использует текущее население, чтобы создать дочерние элементы, которые составляют следующее поколение. Алгоритм выбирает группу индивидуумов в текущем населении, названном родительскими элементами, кто вносит их гены — записи их векторов — их дочерним элементам. Алгоритм обычно выбирает индивидуумов, которые имеют лучшие значения фитнеса как родительские элементы. Можно задать функцию что использование алгоритма, чтобы выбрать родительские элементы в SelectionFcn опция. См. Опции Выбора.
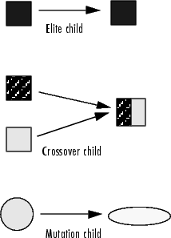
Генетический алгоритм создает три типа дочерних элементов для следующего поколения:
Eliteare индивидуумы в текущем поколении с лучшими значениями фитнеса. Эти индивидуумы автоматически выживают к следующему поколению.
Перекрестное соединение создается путем объединения векторов из пары родительских элементов.
Дочерние элементы мутации создаются путем представления случайных изменений или мутаций, к единому объекту-родителю.
Следующая принципиальная схема иллюстрирует три типа дочерних элементов.
Мутация и Перекрестное соединение объясняют, как задать количество дочерних элементов каждого типа, который алгоритм генерирует и функции, которые это использует, чтобы выполнить перекрестное соединение и мутацию.
Следующие разделы объясняют, как алгоритм создает дочерние элементы перекрестного соединения и мутации.
Алгоритм создает перекрестные дочерние элементы путем объединения пар родительских элементов в текущем населении. В каждой координате дочернего вектора перекрестная функция по умолчанию случайным образом выбирает запись или ген, в той же координате от одного из двух родительских элементов и присваивает его дочернему элементу. Для проблем с линейными ограничениями перекрестная функция по умолчанию создает дочерний элемент как случайное взвешенное среднее родительских элементов.
Алгоритм создает дочерние элементы мутации путем случайного изменения генов отдельных родительских элементов. По умолчанию для неограниченных проблем алгоритм добавляет случайный вектор от Распределения Гаусса до родительского элемента. Для ограниченных или линейно ограниченных проблем дочерний элемент остается выполнимым.
Следующий рисунок показывает дочерние элементы начальной генеральной совокупности, то есть, населения во втором поколении, и указывает, являются ли они элитными, перекрестными, или дочерние элементы мутации.
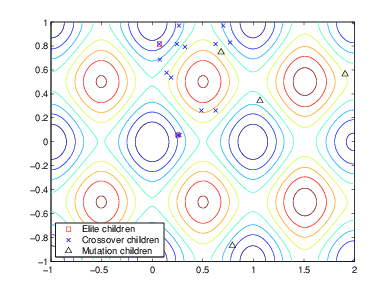
Следующий рисунок показывает популяции в итерациях 60, 80, 95, и 100.
|
|
|
|
|
|
Как количество увеличений поколений, индивидуумы в населении становятся ближе вместе и приближаются к минимальной точке [0 0].
Генетический алгоритм использует следующие опции, чтобы определить, когда остановиться. Смотрите значения по умолчанию для каждой опции путем выполнения opts = optimoptions('ga').
MaxGenerations — Алгоритм останавливается, когда количество поколений достигает MaxGenerations.
MaxTime — Остановки алгоритма после выполнения для количества времени в секундах равняются MaxTime.
FitnessLimit — Алгоритм останавливается, когда значение функции фитнеса для лучшей точки в текущем населении меньше чем или равно FitnessLimit.
MaxStallGenerations — Алгоритм останавливается когда среднее относительное изменение в значении функции фитнеса по MaxStallGenerations меньше Function tolerance.
MaxStallTime — Алгоритм останавливается, если нет никакого улучшения целевой функции в течение интервала времени в секундах, равных MaxStallTime.
FunctionTolerance — Запуски алгоритма до среднего относительного изменения в значении функции фитнеса по MaxStallGenerations меньше Function tolerance.
ConstraintTolerance — ConstraintTolerance не используется в качестве останавливающегося критерия. Это используется, чтобы определить выполнимость относительно нелинейных ограничений. Кроме того, max(sqrt(eps),ConstraintTolerance) определяет выполнимость относительно линейных ограничений.
Алгоритм останавливается, как только любое из этих условий соблюдают.
Функция выбора выбирает родительские элементы для следующего поколения на основе их масштабированных значений от функции масштабирования фитнеса. Масштабированные значения фитнеса называются значениями ожидания. Индивидуум может быть выбран несколько раз как родительский элемент, в этом случае он вносит свои гены больше чем в один дочерний элемент. Опция выбора по умолчанию, @selectionstochunif, размечает линию, в которой каждый родительский элемент соответствует разделу линии длины, пропорциональной ее масштабированному значению. Алгоритм проходит линия с шагом равного размера. На каждом шаге алгоритм выделяет родительский элемент от раздела, на который это приземляется.
Более детерминированной опцией выбора является @selectionremainder, который выполняет два шага:
В первом шаге функция выбирает родительские элементы детерминировано согласно целой части масштабированного значения для каждого индивидуума. Например, если масштабированное значение индивидуума 2.3, функция выбирает того индивидуума дважды как родительский элемент.
На втором шаге функция выбора выбирает дополнительные родительские элементы с помощью дробных частей масштабированных значений, как в стохастическом универсальном выборе. Функция размечает линию в разделах, длины которых пропорциональны дробной части масштабированного значения индивидуумов, и проходит линия на равных шагах, чтобы выбрать родительские элементы.
Обратите внимание на то, что, если дробные части масштабированных значений весь равный 0, как это может произойти с помощью Top при масштабировании выбор совершенно детерминирован.
Для получения дополнительной информации и больше опций выбора, см. Опции Выбора.
Опции воспроизведения управляют, как генетический алгоритм создает следующее поколение. Опции
EliteCount — Количество индивидуумов с лучшими значениями фитнеса в текущем поколении, которые, как гарантируют, выживут к следующему поколению. Эти индивидуумы называются элитными дочерними элементами.
Когда EliteCount по крайней мере 1, лучшее значение фитнеса может только уменьшиться от одной генерации до следующего. Это - то, что вы хотите произойти, поскольку генетический алгоритм минимизирует функцию фитнеса. Установка EliteCount к высоким причинам значения самые подходящие индивидуумы, чтобы доминировать над населением, которое может сделать поиск менее эффективным.
CrossoverFraction — Часть индивидуумов в следующем поколении, кроме элитных дочерних элементов, которые создаются перекрестным соединением. Установка Перекрестной Части описывает как значение CrossoverFraction влияет на эффективность генетического алгоритма.
Поскольку элитные индивидуумы были уже оценены, ga не переоценивает функцию фитнеса элитных индивидуумов во время воспроизведения. Это поведение принимает, что функция фитнеса индивидуума не случайна, но является детерминированной функцией. Чтобы изменить это поведение, используйте выходную функцию. Смотрите EvalElites в структуре состояния.
Генетический алгоритм использует индивидуумов в текущем поколении, чтобы создать дочерние элементы, которые составляют следующее поколение. Помимо элитных дочерних элементов, которые соответствуют индивидуумам в текущем поколении с лучшими значениями фитнеса, алгоритм создает
Перекрестно соедините дочерние элементы путем выбора векторных записей или генов, от пары индивидуумов в текущем поколении, и комбинирует их, чтобы сформировать дочерний элемент
Дочерние элементы мутации путем применения случайных изменений к одному индивидууму в текущем поколении, чтобы создать дочерний элемент
Оба процесса важны для генетического алгоритма. Перекрестное соединение позволяет алгоритму извлечь лучшие гены от различных индивидуумов и повторно объединить их в потенциально превосходящие дочерние элементы. Мутация добавляет к разнообразию населения и таким образом увеличивает вероятность, что алгоритм сгенерирует индивидуумов с лучшими значениями фитнеса.
Смотрите Создание Следующего поколения для примера того, как генетический алгоритм применяет мутацию и перекрестное соединение.
Можно задать, сколько из каждого типа дочерних элементов алгоритм создает можно следующим образом:
EliteCount задает количество элитных дочерних элементов.
CrossoverFraction задает часть населения, кроме элитных дочерних элементов, которые являются перекрестными дочерними элементами.
Например, если PopulationSize 20, EliteCount 2, и CrossoverFraction 0.8, количества каждого типа дочерних элементов в следующем поколении следующие:
Существует два элитных дочерних элемента.
Существует 18 индивидуумов кроме элитных дочерних элементов, таким образом, алгоритм округляется 0.8*18 = 14.4 к 14, чтобы получить количество перекрестных дочерних элементов.
Остающиеся четыре индивидуума, кроме элитных дочерних элементов, являются дочерними элементами мутации.
Когда проблема имеет целочисленные или линейные ограничения (включая границы), алгоритм изменяет эволюцию населения.
Когда проблема имеет и целочисленные и линейные ограничения, программное обеспечение изменяет всех сгенерированных индивидуумов, чтобы быть выполнимым относительно тех ограничений. Можно использовать любое создание, мутацию, или перекрестно соединить функцию, и целое население остается выполнимым относительно целочисленных и линейных ограничений.
Когда проблема имеет только линейные ограничения, программное обеспечение не изменяет индивидуумов, чтобы быть выполнимым относительно тех ограничений. Необходимо использовать создание, мутацию и перекрестные функции, которые обеспечивают выполнимость относительно линейных ограничений. В противном случае население может стать неосуществимым, и результат может быть неосуществимым. Операторы по умолчанию обеспечивают линейную выполнимость: gacreationlinearfeasible или gacreationnonlinearfeasible для создания, mutationadaptfeasible для мутации и crossoverintermediate для перекрестного соединения.
Внутренние алгоритмы для целочисленной и линейной выполнимости похожи на тех для surrogateopt. Когда проблема имеет целочисленные и линейные ограничения, алгоритм сначала создает линейно допустимые точки. Затем алгоритм пытается удовлетворить целочисленным ограничениям путем округления линейно допустимых точек до целых чисел с помощью эвристики, которая пытается сохранить точки линейно выполнимыми. Когда этот процесс неудачен в получении достаточного количества допустимых точек для построения населения, вызовов алгоритма intlinprog пытаться найти больше точек, которые выполнимы относительно границ, линейных ограничений и целочисленных ограничений.
Позже, когда мутация или перекрестное соединение создают новые члены населения, алгоритмы гарантируют, что новые члены являются целым числом и линейный выполнимый путем делания подобных шагов. Каждый новый член изменяется, при необходимости, чтобы быть максимально близким к его исходному значению, также удовлетворяя целочисленным и линейным ограничениям и границам.