"Модели канала распространения

Продукт LTE Toolbox™ обеспечивает набор моделей канала для теста и верификации UE и eNodeB радио-передачи и приема, как задано в [1] и [2]. Следующие модели канала доступны в продукте LTE Toolbox.

Многопутевые исчезающие условия распространения
Условия скоростного поезда
Движущиеся условия распространения

Многопутевые исчезающие условия распространения

Многопутевая исчезающая модель канала задает следующие три профиля задержки.

Расширенный Пешеход модель (EPA)
Расширенный Автомобильный модель (EVA)
Расширенная Типичная Городская модель (ETU)

Эти три профиля задержки представляют минимум, носитель, и высоко задерживают среду распространения, соответственно. Многопутевые профили задержки для этих каналов показывают в следующих таблицах.

Профиль задержки EPA

Избыточная задержка касания (не уточнено)	Относительная степень (дБ)
0	0.0
30	–1.0
70	–2.0
90	–3.0
110	–8.0
190	–17.2
410	–20.8

Профиль задержки ЕВЫ

Избыточная задержка касания (не уточнено)	Относительная степень (дБ)
0	0.0
30	–1.5
150	–1.4
310	–3.6
370	–0.6
710	–9.1
1090	–7.0
1730	–12.0
2510	–16.9

Профиль задержки ETU

Избыточная задержка касания (не уточнено)	Относительная степень (дБ)
0	–1.0
50	–1.0
120	–1.0
200	0.0
230	0.0
500	0.0
1600	–3.0
2300	–5.0
5000	–7.0

Все касания в предыдущих таблицах имеют классический спектр Doppler. В дополнение к многопутевому профилю задержки максимум Доплеровская частота задана для каждого многопутевого исчезающего условия распространения, как показано в следующей таблице.

Модель Channel	Максимум Доплеровская частота
EPA 5 Гц	5 Гц
ЕВА 5 Гц	5 Гц
ЕВА 70 Гц	70 Гц
ETU 70 Гц	70 Гц
ETU 300 Гц	300 Гц

В случае сред MIMO набор корреляционных матриц введен, чтобы смоделировать корреляцию между UE и eNodeB антеннами. Эти корреляционные матрицы введены в Корреляционных матрицах Канала MIMO.

Условие скоростного поезда

Условие скоростного поезда задает не исчезающий канал распространения с одним многопутевым компонентом, положение которого фиксируется вовремя. Этот многопутевой сингл представляет эффект Доплера, который вызывается из-за перемещения скоростного поезда мимо базовой станции как показано в следующем рисунке.

Выражение $D_{s} / 2$ начальное расстояние обучения от eNodeB, и $D_{\min}$ минимальное расстояние между eNodeB и железнодорожным путем. Обе переменные измеряются в метрах. Переменная ν является скоростью обучения в метрах в секунду. Эффект Доплера из-за перемещения обучается, дан в следующем уравнении.

$f_{s} (t) = f_{d} \cos θ (t)$

Переменная $f_{s} (t)$ эффект Доплера и $f_{d}$ максимум Доплеровская частота. Косинус угла $θ (t)$ дан следующим уравнением.

$\cos θ (t) = \frac{D_{s} / 2 - v t}{\sqrt{D_{\min}^{2} + {(D_{s} / 2 - v t)}^{2}}}, 0 \leq t \leq D_{s} / v$

$\cos θ (t) = \frac{- 1.5 D_{s} + v t}{\sqrt{D_{\min}^{2} + {(- 1.5 D_{s} + v t)}^{2}}}, D_{s} / v < t \leq 2 D_{s} / v$

$\cos θ (t) = \cos θ (t \mod (2 D_{s} / v)), t > 2 D_{s} / v$

Для тестирования eNodeB два сценария скоростного поезда заданы, которые используют параметры, перечисленные в следующей таблице. Эффект Доплера, $f_{s} (t)$ , вычисляется с помощью предыдущих уравнений и параметров, перечисленных в следующей таблице.

Параметр	Значение
	Сценарий 1	Сценарий 3
$D_{s}$	1 000 м	300 м
$D_{\min}$	50 м	2 м
ν	350 км/час	300 км/криптон
$f_{d}$	1 340 Гц	1 150 Гц

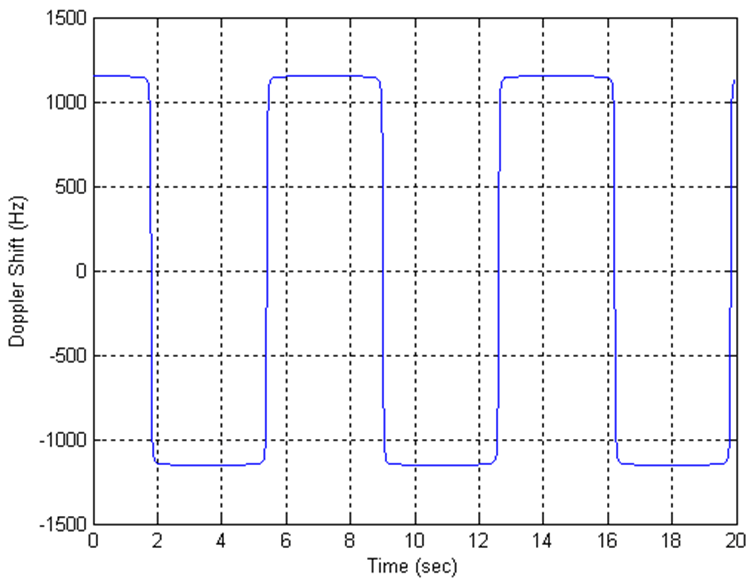
Оба из этих сценариев приводят к эффектам Доплера, которые применяются ко всем диапазонам частот. Траекторию эффекта Доплера для сценария 1 показывают в следующем рисунке.

Траекторию эффекта Доплера для сценария 3 показывают в следующем рисунке.

Для тестирования UE, эффекта Доплера, $f_{s} (t)$ , вычисляется с помощью предыдущих уравнений и параметров, перечисленных в следующей таблице.

Параметр	Значение
$D_{s}$	300 м
$D_{\min}$	2 м
ν	300 км/час
$f_{d}$	750 Гц

Эти параметры приводят к эффекту Доплера, к которому применяются все диапазоны частот, показанные в следующем рисунке.

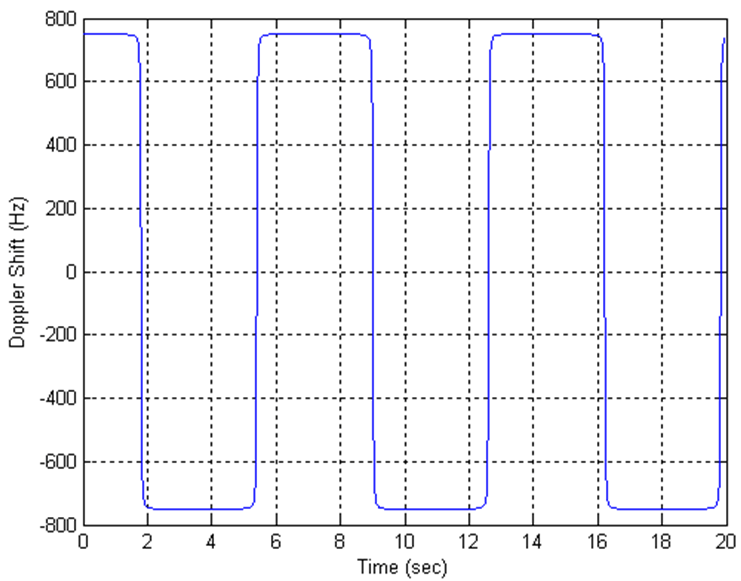
Перемещение условия распространения

Движущийся канал распространения в LTE задает условие канала, где местоположение многопутевых компонентов изменяется. Разница во времени между ссылочным временем и первым касанием, Δτ, дана следующим уравнением.

$Δ τ = \frac{A}{2} \cdot \sin (Δ ω \cdot t)$

Переменная A представляет время начала в секундах, и Δω представляет угловое вращение в радианах в секунду.

Примечание

Относительное время между многопутевыми компонентами остается фиксированным.

Параметры для движущихся условий распространения показывают в следующей таблице.

Параметр	Сценарий 1	Сценарий 2
Модель Channel	ETU200	AWGN
Скорость UE	120 км/час	350 км/час
Длина CP	Нормальный	Нормальный
A	10 μs	10 μs
Δω	0,04 с^–1	0,13 с^–1

Эффект Доплера только применяется к генерации исчезающих выборок для сценария 1. В сценарии 2 моделируется один не исчезающий многопутевой компонент с аддитивным белым гауссовым шумом (AWGN). Местоположение этого многопутевого компонента изменяется со временем, согласно предыдущему уравнению.

Пример движущегося канала с одним неисчезающим касанием показывают в следующем рисунке.

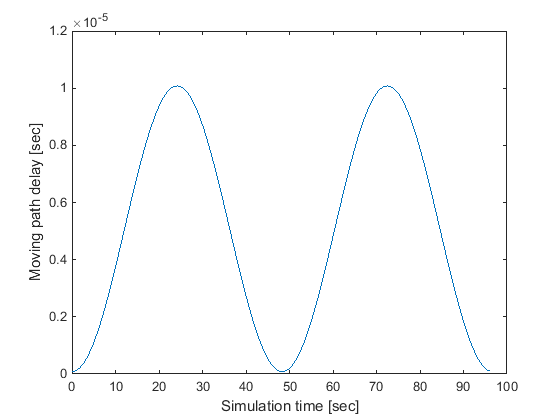
Корреляционные матрицы канала MIMO

В системах MIMO между передающими и приемными антеннами существует корреляция. Это зависит от ряда факторов, такие как разделение между антенной и несущей частотой. Для максимальной способности желательно минимизировать корреляцию между передающими и приемными антеннами.

Существуют различные способы смоделировать корреляцию антенны. Один метод использует корреляционные матрицы, чтобы описать корреляцию между несколькими антеннами и в передатчике и в приемнике. Эти матрицы вычислены независимо и в приемнике передатчика и в затем объединены посредством Кронекерова продукта для того, чтобы сгенерировать канал пространственная корреляционная матрица.

Три различных уровня корреляции заданы в [1].

низко или никакая корреляция
средняя корреляция
высокая корреляция

Параметры α и β заданы для каждого уровня корреляции как показано в следующей таблице значений корреляции.

Низкая корреляция		Средняя корреляция		Высокая корреляция
α	β	α	β	α	β
0	0	0.3	0.9	0.9	0.9

Независимые корреляционные матрицы в eNodeB и UE, _ReNB и _RUE, соответственно, показывают для различного набора антенн (1, 2 и 4) в следующей таблице.

Корреляция	Одна антенна	Две антенны	Четыре антенны
eNodeB	$R_{e N B} = 1$	$R_{e N B} = (\begin{array}{l} 1 α \\ α^{*} 1 \end{array})$	$R_{e N B} = (\begin{matrix} 1 & α^{\frac{1}{9}} & α^{\frac{4}{9}} & α \\ α^{\frac{1}{9}}^{} & 1 & α^{\frac{1}{9}} & α^{\frac{4}{9}} \\ α^{\frac{4}{9}}^{} & α^{\frac{1}{9}}^{} & 1 & α^{\frac{1}{9}} \\ α^{} & α^{\frac{4}{9}}^{} & α^{\frac{1}{9}}^{} & 1 \end{matrix})$
UE	$R_{U E} = 1$	$R_{U E} = (\begin{array}{l} 1 β \\ β^{*} 1 \end{array})$	$R_{U E} = (\begin{matrix} 1 & β^{\frac{1}{9}} & β^{\frac{4}{9}} & β \\ β^{\frac{1}{9}}^{} & 1 & β^{\frac{1}{9}} & β^{\frac{4}{9}} \\ β^{\frac{4}{9}}^{} & β^{\frac{1}{9}}^{} & 1 & β^{\frac{1}{9}} \\ β^{} & β^{\frac{4}{9}}^{} & β^{\frac{1}{9}}^{} & 1 \end{matrix})$

Канал пространственная корреляционная матрица, _Rspat, дан следующим уравнением.

$R_{s p a t} = R_{e N B} \otimes R_{U E}$

Символ ⊗ представляет продукт Kronecker. Значения канала пространственная корреляционная матрица, _Rspat, для различных матричных размеров заданы в следующей таблице.

MatrixSize	Значения _Rspat
1×2 случай	$R_{s p a t} = R_{U E} = (\begin{matrix} 1 & β \\ β^{*} & 1 \end{matrix})$
2×2 случай	$R_{s p a t} = R_{e N B} \otimes R_{U E} = (\begin{matrix} 1 & α \\ α^{} & 1 \end{matrix}) \otimes (\begin{matrix} 1 & β \\ β^{} & 1 \end{matrix}) = (\begin{matrix} 1 & β & α & α β \\ β^{} & 1 & α β^{} & α \\ α^{} & α^{} β & 1 & β \\ α^{} β^{} & α^{} & β^{} & 1 \end{matrix})$
4×2 случай	$R_{s p a t} = R_{e N B} \otimes R_{U E} = (\begin{matrix} 1 & α^{\frac{1}{9}} & α^{\frac{4}{9}} & α \\ α^{\frac{1}{9}}^{} & 1 & α^{\frac{1}{9}} & α^{\frac{4}{9}} \\ α^{\frac{4}{9}}^{} & α^{\frac{1}{9} } & 1 & α^{\frac{1}{9}} \\ α^{} & α^{\frac{4}{9}}^{} & α^{\frac{1}{9}}^{} & 1 \end{matrix}) \otimes (\begin{matrix} 1 & β \\ β^{*} & 1 \end{matrix})$
4×4 случай	$R_{s p a t} = R_{e N B} \otimes R_{U E} = (\begin{matrix} 1 & α^{\frac{1}{9}} & α^{\frac{4}{9}} & α \\ α^{\frac{1}{9}}^{} & 1 & α^{\frac{1}{9}} & α^{\frac{4}{9}} \\ α^{\frac{4}{9}}^{} & α^{\frac{1}{9} } & 1 & α^{\frac{1}{9}} \\ α^{} & α^{\frac{4}{9}}^{} & α^{\frac{1}{9}}^{} & 1 \end{matrix}) \otimes (\begin{matrix} 1 & β^{\frac{1}{9}} & β^{\frac{4}{9}} & β \\ β^{\frac{1}{9}}^{} & 1 & β^{\frac{1}{9}} & β^{\frac{4}{9}} \\ β^{\frac{4}{9}}^{} & β^{\frac{1}{9} } & 1 & β^{\frac{1}{9}} \\ β^{} & β^{\frac{4}{9}}^{} & β^{\frac{1}{9}}^{} & 1 \end{matrix})$

Ссылки

[1] 3GPP TS 36.101. “Развитый Универсальный Наземный Радио-доступ (к E-UTRA); Передача Радио Оборудования пользователя (UE) и Прием”. Проект Партнерства третьего поколения; Сеть радиодоступа Technical Specification Group. URL: https://www.3gpp.org.

[2] 3GPP TS 36.104. “Развитый Универсальный Наземный Радио-доступ (к E-UTRA); Передача Радио Базовой станции (BS) и Прием”. Проект Партнерства третьего поколения; Сеть радиодоступа Technical Specification Group. URL: https://www.3gpp.org.

Документация