Сигналы синхронизации (PSS и SSS)

В LTE существует два нисходящих сигнала синхронизации, которые используются UE, чтобы получить идентичность ячейки и синхронизацию системы координат.

Первичный сигнал синхронизации (PSS)
Вторичный сигнал синхронизации (SSS)

Деление на два сигнала нацелено, чтобы уменьшать сложность процесса поиска ячейки.

Единичное расположение ячейки

Физическая идентичность ячейки, $N_{I D}^{c e l l}$ , задан уравнением:

$N_{I D}^{C E L L} = 3 N_{I D}^{(1)} + N_{I D}^{(2)}$

$N_{I D}^{(1)}$ единичная группа ячейки физического уровня (от 0 до 167).
$N_{I D}^{(2)}$ идентичность в группе (от 0 до 2).

Это расположение создает 504 уникальных физических тождеств ячейки.

Сигналы синхронизации и определение идентичности ячейки

Первичный сигнал синхронизации (PSS) соединяется с идентичностью ячейки в группе ( $N_{I D}^{(2)}$ ). Вторичный сигнал синхронизации (SSS) соединяется с единичной группой ячейки ( $N_{I D}^{(1)}$ ) и идентичность ячейки в группе ( $N_{I D}^{(2)}$ ).

Можно получить $N_{I D}^{(2)}$ путем успешной демодуляции PSS. SSS может затем демодулироваться и объединяться со знанием $N_{I D}^{(2)}$ получить $N_{I D}^{(1)}$ . Если вы устанавливаете значения $N_{I D}^{(1)}$ и $N_{I D}^{(2)}$ , можно определить идентичность ячейки ( $N_{I D}^{c e l l}$ ).

Первичный сигнал синхронизации (PSS)

Первичный сигнал синхронизации (PSS) основан на Последовательности Задова-Чу частотного диапазона.

Последовательности Задова-Чу

Последовательности Задова-Чу являются конструкцией последовательностей Фрэнка-Зэдофф, заданных Д. Ц. Чу в [1]. Эти коды имеют полезное свойство наличия нулевой циклической автокорреляции во всех ненулевых задержках. Когда используется в качестве кода синхронизации, корреляции между идеальной последовательностью и полученной последовательностью является самым большим, когда задержка является нулем. Когда существует любая задержка между этими двумя последовательностями, корреляция является нулем. Это свойство проиллюстрировано в этом рисунке.

Генерация PSS

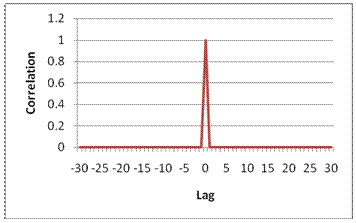
PSS является последовательностью комплексных символов, 62 символа долго.

Последовательность $d_{u} (n)$ используемый для PSS сгенерирован согласно этим уравнениям:

$d_{u} (n) = e^{- j \frac{π u n (n + 1)}{63}}, для n = 0, 1, \dots, 30$

$d_{u} (n) = e^{- j \frac{π u (n + 1) (n + 2)}{63}}, для n = 31, 32, \dots, 61$

В предыдущем уравнении u является корневым индексом последовательности Zadoff-Чу и зависит от идентичности ячейки в группе $N_{I D}^{(2)}$ .

$N_{I D}^{(2)}$	Корневой индекс u
0	25
1	29
2	34

Отображение PSS

PSS сопоставлен в первую 31 поднесущую любая сторона поднесущей DC. Поэтому PSS использует шесть блоков ресурса с пятью зарезервированными поднесущими каждая сторона, как показано в этом рисунке.

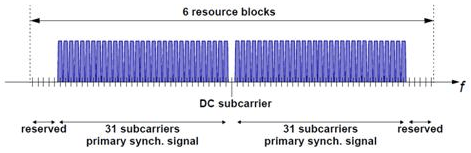
Когда поднесущая DC не содержит информации в LTE, это соответствует отображению на средние 62 поднесущих в символе OFDM в сетке ресурса. d (n) сопоставлен от самой низкой поднесущей до самой высокой поднесущей. PSS сопоставлен с различными символами OFDM, в зависимости от которых используется тип системы координат. Тип 1 системы координат является дуплексом деления частоты (FDD), и тип 2 системы координат является дуплексом деления времени (TDD).

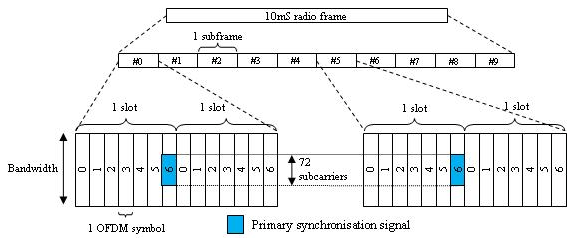
FDD — PSS сопоставлен с последним символом OFDM в пазах 0 и 10, как показано в этом рисунке.
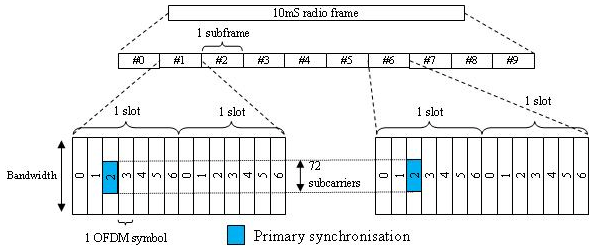
TDD — PSS сопоставлен с третьим символом OFDM в подкадрах 1 и 6, как показано в этом рисунке.

Вторичный сигнал синхронизации (SSS)

Вторичный сигнал синхронизации (SSS) основан на максимальных последовательностях длины (m - последовательности).

M- определение последовательности

m - последовательность является псевдослучайной двоичной последовательностью, которая может быть создана путем циклического повторения через каждое возможное состояние сдвигового регистра длины m, приведения к последовательности длины 2^m– 1. Три m - последовательности, каждая длина 31, используются, чтобы сгенерировать обозначенные сигналы синхронизации $\tilde{s}$ , $\tilde{c}$ и $\tilde{z}$ .

Генерация SSS

Две двоичных последовательности, каждая длина 31, используются, чтобы сгенерировать SSS. Последовательности s ₀^(m₀) и s ₁^(m₁) различные циклические сдвиги m - последовательность, $\tilde{s}$ . Индексы m ₀ и m ₁ выведены из группы идентичности ячейки, _NID⁽²⁾ и определите циклический сдвиг. Значения могут быть считаны из таблицы 6.11.2.1-1 в [2].

Эти две последовательности скремблированы с двоичным кодом скремблирования (c ₀ (n), c ₁ (n)), который зависит от _NID⁽²⁾.

Вторая последовательность SSS, используемая в каждой радио-системе координат, скремблирована с двоичным кодом скремблирования (z ₁^(m₀), z ₁^(m₁)) соответствие значению циклического сдвига первой последовательности передается в радио-системе координат.

Генерация двоичной последовательности

Последовательности s ₀^(m₀) и s ₁^(m₁) даны этими уравнениями:

$s_{0}^{(m_{0})} (n) = \tilde{s} ((n + m_{0}) mod 31)$

$s_{1}^{(m_{1})} (n) = \tilde{s} ((n + m_{1}) mod 31)$

$\tilde{s}$ сгенерирован от примитивного полинома $x^{5} + x^{2} + 1$ по конечному полю GF (2).

c ₀ (n) и c ₁ (n даны этими уравнениями:

$c_{0} (n) = \tilde{c} ((n + N_{ID}^{(2)}) mod 31)$

$c_{1} (n) = \tilde{c} ((n + N_{ID}^{(2)} + 3) mod 31)$

$\tilde{c}$ сгенерирован от примитивного полинома $x^{5} + x^{3} + 1$ по конечному полю GF (2).

z ₁^(m₀) и z ₁^(m₁) даны этими уравнениями:

$z_{1}^{(m_{0})} (n) = \tilde{z} ((n + (m_{0} mod 8)) mod 31)$

$z_{1}^{(m_{1})} (n) = \tilde{z} ((n + (m_{1} mod 8)) mod 31)$

$\tilde{z}$ сгенерирован от примитивного полинома $x^{5} + x^{4} + x^{2} + x + 1$ по конечному полю GF (2).

Отображение SSS

Скремблированные последовательности чередованы, чтобы чередовать последовательность, переданную в первой и второй передаче SSS в каждой радио-системе координат. Это позволяет приемнику определять синхронизацию системы координат из наблюдения только одной из этих двух последовательностей; если первый наблюдаемый сигнал SSS находится в подкадре 0 или подкадре 5, синхронизация может быть достигнута, когда сигнал SSS наблюдается в подкадре 0 или подкадре 5 из следующей системы координат.

Как с PSS, SSS сопоставлен с различными символами OFDM, в зависимости от которых используется тип системы координат:

FDD — SSS передается в том же подкадре как PSS, но один символ OFDM ранее. SSS сопоставлен с теми же поднесущими (средние 72 поднесущие) как PSS.
TDD — SSS сопоставлен с последним символом OFDM в пазах 1 и 11, который является тремя символами OFDM перед PSS.

SSS создается с помощью различных последовательностей скремблирования, когда сопоставлено с четными и нечетными элементами ресурса.

Даже элементы ресурса:
- Подкадр 0: $d (2 n) = s_{0}^{(m_{0})} (n) c_{0} (n)$
- Подкадр 5: $d (2 n) = s_{1}^{(m_{1})} (n) c_{0} (n)$
Нечетные элементы ресурса:
- Подкадр 0: $d (2 n + 1) = s_{1}^{(m_{1})} (n) c_{1} (n) z_{1}^{(m_{0})} (n)$
- Подкадр 5: $d (2 n + 1) = s_{0}^{(m_{0})} (n) c_{1} (n) z_{1}^{(m_{1})} (n)$

d (n) сопоставлен от самой низкой поднесущей до самой высокой поднесущей.

Ссылки

[1] Чу, D. C. “Многофазные коды с хорошими периодическими свойствами корреляции”. Сделка IEEE Inf. Теория. Издание 18, Номер 4, июль 1972, стр 531–532.

[2] 3GPP TS 36.211. “Развитый Универсальный Наземный Радио-доступ (к E-UTRA); Физические Каналы и Модуляция”. Проект Партнерства третьего поколения; Сеть радиодоступа Technical Specification Group. URL: https://www.3gpp.org.

Документация