Одно из большинства важных и распространенных приложений числовой линейной алгебры является решением линейных систем, которые могут быть описаны в форме A*x = b. Когда A большая разреженная матрица, можно решить линейную систему с помощью итерационных методов, которые включают вам к компромиссу между временем выполнения вычисления и точностью решения. Эта тема описывает итерационные методы, доступные в MATLAB® решить уравнение A*x = b.
Существует два типа методов для решения линейных уравнений A*x = b:
Прямые методы являются вариантами Исключения Гаусса. Эти методы используют отдельные элементы матрицы непосредственно, посредством операций над матрицей, таких как LU, QR или факторизация Холесского. Можно использовать прямые методы решить линейные уравнения с высоким уровнем точности, но эти методы могут быть медленными при работе с большими разреженными матрицами. Скорость решения линейной системы с прямым методом строго зависит от плотности и узора заливки матрицы коэффициентов.
Например, этот код решает маленькую линейную систему.
A = magic(5); b = sum(A,2); x = A\b; norm(A*x-b)
ans = 1.4211e-14
MATLAB реализует прямые методы через матричные операторы деления / и \, а также функционирует, такие как decomposition, lsqminnorm, и linsolve.
Итерационные методы производят приближенное решение линейной системы после конечного числа шагов. Эти методы полезны для больших систем уравнений, где это разумно к точности компромисса в течение более короткого времени выполнения. Итерационные методы используют матрицу коэффициентов только косвенно посредством матричного векторного произведения или абстрактного линейного оператора. Итерационные методы могут использоваться с любой матрицей, но они обычно применяются к большим разреженным матрицам, для которых прямой решает, являются медленными. Скорость решения линейной системы с косвенным методом не зависит так же строго от узора заливки матрицы коэффициентов как прямой метод. Однако использование итерационного метода обычно требует настраивающихся параметров для каждой определенной проблемы.
Например, этот код решает большую разреженную линейную систему, которая имеет симметричную положительную определенную матрицу коэффициентов.
A = delsq(numgrid('L',400));
b = ones(size(A,1),1);
x = pcg(A,b,[],1000);
norm(b-A*x)pcg converged at iteration 796 to a solution with relative residual 9.9e-07. ans = 3.4285e-04
MATLAB реализует множество итерационных методов, которые имеют различные достоинства и недостатки в зависимости от свойств матрицы коэффициентов A.
Прямые методы обычно быстрее и в более общем плане применимы, чем косвенные методы, если существует достаточно устройства хранения данных, доступного, чтобы выполнить их. Обычно необходимо попытаться использовать x = A\b сначала. Если прямые решают, является слишком медленным, то можно попытаться использовать итерационные методы.
Большинство итеративных алгоритмов, которые решают линейные уравнения, следует за подобным процессом:
Начните с исходного предположения для вектора решения x0. (Это обычно - нулевой вектор, если вы не задаете лучшее предположение.)
Вычислите норму невязки res = norm(b-A*x0).
Сравните невязку с заданным допуском. Если res <= tol, закончите расчет и дайте вычисленный ответ для x0.
Примените A*x0 и обновите величину и направление векторного x0 на основе значения невязки и других расчетных количеств. Это - шаг, где большая часть расчета сделана.
Повторите Шаги 2 - 4 до значения x0 достаточно хорошо, чтобы удовлетворить допуску.
Итерационные методы отличаются по тому, как они обновляют величину и направление x0 на Шаге 4, и у некоторых есть немного отличающиеся критерии сходимости на Шагах 2 и 3, но это получает базовый процесс, за которым следуют все итеративные решатели.
MATLAB имеет несколько функций, которые реализуют итерационные методы для систем линейных уравнений. Эти методы спроектированы, чтобы решить A x = b или минимизировать норму || b – A x ||. Несколько из этих методов имеют общие черты и основаны на тех же базовых алгоритмах, но каждый алгоритм обладает преимуществами в определенных ситуациях [1], [2].
Описание | Примечания |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
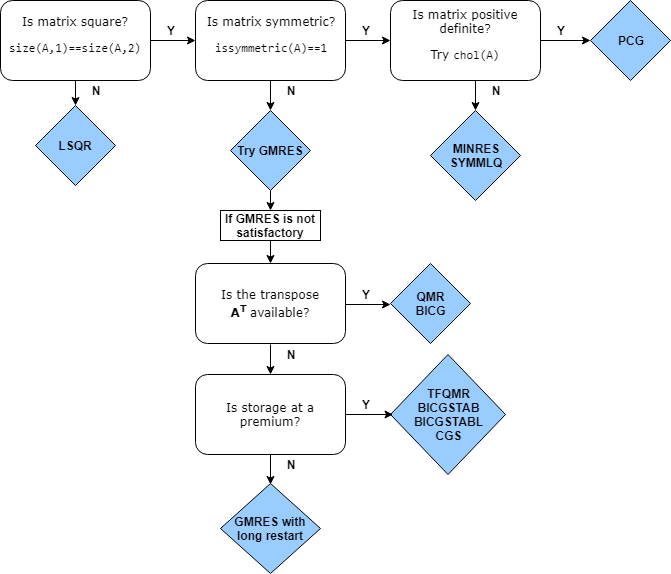
Эта блок-схема итеративных решателей в MATLAB дает общее представление о ситуациях, где каждый решатель полезен. Можно обычно использовать gmres почти для всех квадратных, несимметричных проблем. Существуют некоторые случаи где бисопряженные алгоритмы градиентов (bicg, bicgstab, cgs, и так далее), более эффективны, чем gmres, но их непредсказуемое поведение сходимости часто делает gmres лучший начальный выбор.
Уровень сходимости итерационных методов зависит от спектра (собственные значения) матрицы коэффициентов. Поэтому можно улучшить сходимость и устойчивость большинства итерационных методов путем преобразования линейной системы, чтобы иметь более благоприятный спектр (кластеризируемые собственные значения или число обусловленности около 1). Это преобразование выполняется путем применения второй матрицы, названной preconditioner, к системе. Этот процесс преобразовывает линейную систему
в эквивалентную систему
Идеальный предварительный формирователь преобразовывает матрицу коэффициентов A в единичную матрицу, поскольку любой итерационный метод будет сходиться в одной итерации с таким предварительным формирователем. На практике нахождение хорошего предварительного формирователя требует компромиссов. Преобразование выполняется одним из трех способов: оставленное предварительное создание условий, правильное предварительное создание условий или предварительное создание условий разделения.
Первый случай называется оставленным предварительным созданием условий начиная с матрицы перед формирователем, M появляется слева от A:
Эти итеративные решатели использование оставили предварительное создание условий:
В правильном предварительном создании условий M появляется справа от A:
Эти итеративные решатели используют правильное предварительное создание условий:
Наконец, для симметричных содействующих матриц A, разделите предварительное создание условий гарантирует, что преобразованная система все еще симметрична. Предварительный формирователь разделен и факторы появляются на различных сторонах A:
Алгоритм решателя для разделения, которое предобусловленные системы на основе вышеупомянутого уравнения, но на практике нет никакой потребности вычислить H. Алгоритм решателя умножает и решает с M непосредственно.
Эти итеративные решатели используют предварительное создание условий разделения:
Во всех случаях предварительный формирователь M выбран, чтобы ускорить сходимость итерационного метода. Когда остаточная ошибка итеративного решения застаивается или делает небольшой прогресс между итерациями, это часто означает, что необходимо сгенерировать матрицу перед формирователем, чтобы соединиться в проблему.
Итеративные решатели в MATLAB позволяют вам задавать одну матрицу перед формирователем M, или две матрицы перед формирователем учитывают таким образом что M = M 1M2. Это дает возможность задавать предварительный формирователь в его разложенной на множители форме, такой как M = L U. Обратите внимание на то, что в разделении предобусловленный случай, где M = H HT также содержит, между M1 нет отношения и M2 входные параметры и факторы H.
В некоторых случаях предварительные формирователи происходят естественно в математической модели данной проблемы. В отсутствие естественных предварительных формирователей можно использовать одну из неполных факторизаций в этой таблице, чтобы сгенерировать матрицу перед формирователем. Неполные факторизации чрезвычайно неполные прямой, решает, которые быстры, чтобы вычислить.
| Функция | Факторизация | Описание |
|---|---|---|
ilu |
| Неполная LU-факторизация для квадратных или прямоугольных матриц. |
ichol |
| Неполная факторизация Холесского для симметричных положительных определенных матриц. |
Смотрите Неполные Факторизации для получения дополнительной информации о ilu и ichol.
Рассмотрите приближение конечной разности с пятью точками к уравнению Лапласа на квадратной, двумерной области. Следующие команды используют метод предобусловленного метода сопряженных градиентов (PCG) с предварительным формирователем M = L*L', где L заполнение нулями неполного Фактора Холецкого A. Для этой системы, pcg не может найти решение, не задавая матрицу перед формирователем.
A = delsq(numgrid('S',250));
b = ones(size(A,1),1);
tol = 1e-3;
maxit = 100;
L = ichol(A);
x = pcg(A,b,tol,maxit,L,L');pcg converged at iteration 92 to a solution with relative residual 0.00076.
pcg требует, чтобы 92 итерации достигли заданного допуска. Однако использование различного предварительного формирователя может привести к лучшим результатам. Например, использование ichol создать модифицированный неполный Холесский позволяет pcg соответствовать заданному допуску только после 39 итераций.
L = ichol(A,struct('type','nofill','michol','on')); x = pcg(A,b,tol,maxit,L,L');
pcg converged at iteration 39 to a solution with relative residual 0.00098.
Для в вычислительном отношении жестких проблем вам может быть нужен лучший предварительный формирователь, чем тот, сгенерированный ilu или ichol непосредственно. Например, вы можете хотеть сгенерировать лучший качественный предварительный формирователь или минимизировать объем сделанного расчета. В этих случаях можно использовать уравновешивание, чтобы сделать матрицу коэффициентов более по диагонали доминирующей (который может привести к лучшему качественному предварительному формирователю), и переупорядочивающий, чтобы минимизировать количество ненулей в матричных факторах (который может уменьшать требования к памяти и может повысить эффективность последующих вычислений).
Если вы используете и уравновешивание и переупорядочивающий, чтобы сгенерировать предварительный формирователь, процесс:
Использование equilibrate на матрице коэффициентов.
Переупорядочьте уравновешенную матрицу с помощью функции переупорядочения разреженной матрицы, такой как dissect или symrcm.
Сгенерируйте итоговое использование перед формирователем ilu или ichol.
Вот пример, который использует уравновешивание и переупорядочивающий, чтобы сгенерировать предварительный формирователь для разреженной матрицы коэффициентов.
Создайте матрицу коэффициентов A и вектор из единиц b для правой стороны линейного уравнения. Вычислите оценку числа обусловленности для A.
load west0479;
A = west0479;
b = ones(size(A,1),1);
condest(A)ans = 1.4244e+12
Использование equilibrate улучшить число обусловленности матрицы коэффициентов.
[P,R,C] = equilibrate(A); Anew = R*P*A*C; bnew = R*P*b; condest(Anew)
ans = 5.1042e+04
Переупорядочьте уравновешенное матричное использование dissect.
q = dissect(Anew); Anew = Anew(q,q); bnew = bnew(q);
Сгенерируйте предварительный формирователь с помощью неполной LU-факторизации.
[L,U] = ilu(Anew);
Решите линейную систему с gmres с помощью матриц перед формирователем, допуска 1e-10, 50 максимальных внешних итераций и 30 внутренних итераций.
tol = 1e-10; maxit = 50; restart = 30; [xnew, flag, relres] = gmres(Anew,bnew,restart,tol,maxit,L,U); x(q) = xnew; x = C*x(:);
Теперь сравните relres относительная невязка, возвращенная gmres (который включает предварительные формирователи) к относительной невязке без предварительных формирователей resnew и относительная невязка без уравновешивания res. Результаты показывают, что даже при том, что линейные системы являются всем эквивалентом, различные методы применяют различные веса к каждому элементу, и это может значительно влиять на значение невязки.
relres resnew = norm(Anew*xnew - bnew) / norm(bnew) res = norm(A*x - b) / norm(b)
relres = 8.7537e-11 resnew = 3.6805e-08 res = 5.1415e-04
Итеративные решатели в MATLAB не требуют, чтобы вы обеспечили числовую матрицу для A. Поскольку вычисления, выполняемые решателями, используют результат матричного векторного умножения A*x или A'*x, можно вместо этого обеспечить функцию, которая вычисляет результат тех линейных операций. Функция, которая вычисляет эти количества, часто вызывается linear operator.
В дополнение к использованию линейного оператора вместо матрицы коэффициентов A, можно также использовать линейный оператор вместо матрицы для предварительного формирователя M. В этом случае функция должна вычислить M\x или M'\x, как обозначено на странице с описанием для решателя.
Используя линейные операторы позволяет вам использовать шаблоны в A или M вычислить значение линейных операций более эффективно, чем если бы решатель использовал матрицу явным образом, чтобы выполнить полное матричное векторное умножение. Это также означает, что вам не нужна память, чтобы сохранить коэффициент или матрицы перед формирователем, поскольку линейный оператор обычно вычисляет результат матричного векторного умножения, не формируя матрицу вообще.
Например, рассмотрите матрицу коэффициентов
A = [2 -1 0 0 0 0;
-1 2 -1 0 0 0;
0 -1 2 -1 0 0;
0 0 -1 2 -1 0;
0 0 0 -1 2 -1;
0 0 0 0 -1 2];Когда A умножает вектор, большинством элементов в итоговом векторе являются нули. Ненулевые элементы в результате соответствуют ненулевым трехдиагональным элементам A. Так, для данного векторного x, функция линейного оператора просто должна добавить вместе три вектора, чтобы вычислить значение A*x:
function y = linearOperatorA(x) y = -1*[0; x(1:end-1)] ... + 2*x ... + -1*[x(2:end); 0]; end
Большинство итеративных решателей требует функции линейного оператора для A возвращать значение A*x. Аналогично, для матрицы перед формирователем M, функция обычно должна вычислять M\x. Для решателей lsqr, qmr, и bicg, функции линейного оператора должны также возвратить значение для A'*x или M'\x когда требуется. Смотрите итеративные страницы с описанием решателя для примеров и описаний функций линейного оператора.
[1] Барретт, R., М. Берри, Т. Ф. Чан, и др., Шаблоны для Решения Линейных систем: Базовые блоки для Итерационных методов, SIAM, Филадельфия, 1994.
[2] Саад, Yousef, итерационные методы для разреженных линейных уравнений. PWS Publishing Company, 1996.