Модель CSTR

Адиабатический непрерывный реактор смесителя (CSTR) является общей химической системой в перерабатывающей промышленности, и это описано экстенсивно в [1]. Одна экзотермическая и необратимая реакция первого порядка, → B, происходит в судне, которое принято, чтобы быть всегда отлично смешанным. Входной поток реагента A вводит бак на постоянном объемном уровне. Поток продукта B выходы постоянно на том же объемном уровне и жидкой плотности является постоянным. Таким образом объем реагирующей жидкости является постоянным. Следующий рисунок показывает принципиальную схему судна и конверта охлаждения окружения.

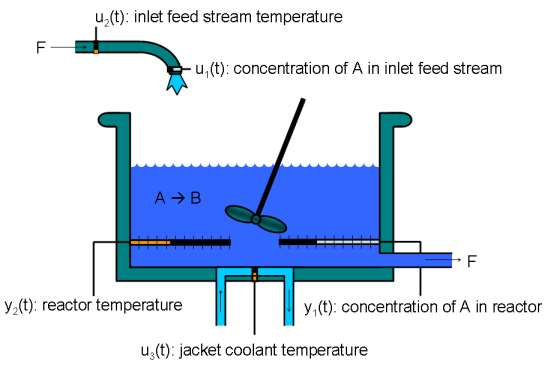
Basic schematic diagram of a CSTR plant showing the inlet feed stream feeding the vessel, surrounded by the cooling jacket. The coolant flows through the cooling jacket to keep the jacket and the reactor cool.

Входные параметры модели CSTR располагаются в векторном u (t) и можно следующим образом.

_u1 – _CAf, концентрация реагента во входе питает поток, измеренный в kmol/m³
_u2 – _Tf, температура входа питает поток, измеренный в K
_u2 – _Tc, температура хладагента конверта, измеренного в K

Первые два входных параметров (концентрация и температура входного потока канала реагента, иногда также обозначенного как _CAi и _Ti, соответственно), обычно принимаются постоянным неизмеренные воздействия, в то время как третьим (температура хладагента) является вход управления, используемый, чтобы управлять процессом. Обратите внимание на то, что схема является упрощенным эскизом; в действительности поток хладагента окружает целый реакторный конверт, и не только нижнюю часть его.

Состояния модели располагаются в векторном x (t).

_x1 _CA, концентрация реагента в реакторе, измеренном в kmol/m³
_x2 T, температура в реакторе, измеренном в K

Нелинейная модель

Система CSTR моделируется с помощью баланса основной массы и принципов энергосбережения. Изменение концентрации реагента в судне на единицу измерения времени может быть смоделировано можно следующим образом.

$\frac{d C_{A}}{d t} = \frac{F}{V} (C_{A f} (t) - C_{A} (t)) - r (t)$

Первый термин, где V является реакторным объемом и F, является объемным расходом, описывает различие в концентрации между входом и потоком. Второй термин является скоростью реакции на модуль объема, и это описано законом об уровне Аррениуса, можно следующим образом.

$r (t) = k_{0} e^{\frac{- E}{R T (t)}} C_{A} (t)$

Здесь:

E является энергией активации.
R является постоянным газом идеала Больцманна.
T является температурой в реакторе.
_k0 является неизвестной нетепловой константой.

Закон об уровне утверждает, что скорость реакции увеличивается экспоненциально с абсолютной температурой.

Точно так же с помощью энергетического принципа баланса, и принимая постоянный объем в реакторе, изменение температуры на модуль времени может быть смоделировано можно следующим образом.

$\frac{d T (t)}{d t} = \frac{F}{V} (T_{f} (t) - T (t)) - \frac{Δ H}{ρ C_{p}} r (t) - \frac{U A}{ρ C_{p} V} (T (t) - T_{c} (t))$

Здесь, первые и третьи термины описывают изменения из-за входной потоковой температуры канала _Tf и температура хладагента конверта _Tc, соответственно. Второй термин представляет влияние на реакторную температуру, вызванную химической реакцией в судне.

В этом уравнении:

ΔH является теплом реакции на моль.
_Cp является коэффициентом теплоемкости.
ρ является коэффициентом плотности.
U является полным коэффициентом теплопередачи.
A является областью для теплообмена (область интерфейса хладагента/судна).

Simulink^® представление этой нелинейной реакторной модели доступно в моделях mpc_cstr_plant, CSTR_OpenLoop, и CSTR_INOUT. Это используется в нескольких примерах, иллюстрирующих, как линеаризовать нелинейные модели и как использовать линейный, адаптивный, запланированный на усиление, и нелинейный MPC, чтобы управлять нелинейным объектом.

Параметры нелинейной модели Simulink CSTR

Параметр	Значение	Модуль	Описание
F	1	m³H	Объемный расход
V	1	m³	Реакторный объем
R	1.985875	kcal / (kmol · K	Идеальная газовая константа Больцманна
ΔH	-5,960	kcal/kmol	Тепло реакции на моль
E	11,843	kcal/kmol	Энергия активации на моль
_k0	34,930,800	1/h	Предэкспоненциальный нетепловой фактор
_ρCp	500	kcal / (m³K	Плотность умножается на теплоемкость
UA	150	kcal / (K · h	Полный коэффициент теплопередачи умножается на область бака

В модели начальное значение _CA является 8.5698 kmol/m³ и начальное значение для T является 311.2639 K. Эта рабочая точка является равновесием, когда концентрация канала притока _CAf является 10 kmol/m³, температура канала притока _Tf является 300 K и температурой хладагента _Tc, является 292 K.

В примере Неадиабатический Непрерывный Реактор Смесителя: Моделирование файла MATLAB с Симуляциями в Simulink® (System Identification Toolbox), вы используете вышеупомянутые уравнения, чтобы оценить последние четыре параметра, когда воздействие вводит _CAf, и _Tf остаются вокруг к 10 kmol/m³ и 298 K, соответственно, и вход _Tc управления лежат в диапазоне от 273 до 322 K. Первая переменная состояния, _CA, лежит в диапазоне от 0 до 10 kmol/m³ и второй, T, лежит в диапазоне от 310 до 390 K. Значения последних четырех параметров, как оценивается, 11,854, 35,588,869, 500.7095, и 150.1275, соответственно, с теми же модулями как в таблице.

Линейная модель

Линеаризовавшая модель CSTR, в котором _Tf не отклоняется от своего номинального условия, может быть представлена следующими линейными дифференциальными уравнениями.

$\frac{d {C^{'}}_{A}}{d t} = a_{11} {C^{'}}_{A} + a_{12} T^{'} + b_{11} {T^{'}}_{c} + b_{12} {C^{'}}_{A i}$

$\frac{d T^{'}}{d t} = a_{21} {C^{'}}_{A} + a_{22} T^{'} + b_{21} {T^{'}}_{c} + b_{22} {C^{'}}_{A i}$

Здесь, начала (например, C ′_A) обозначают отклонение от номинального установившегося условия, при котором линеаризовалась модель. Константы _aij и _bij являются коэффициентами якобиевских матриц (обычно обозначенный как A и B) относительно состояния и входа, соответственно. Символьное выражение большинства этих коэффициентов дано в [1].

Поскольку измерение концентраций реагента часто затрудняет, общее предположение - то, что T является единственный измеренный выход, в то время как _CA не измерен. По подобным причинам _CAf обычно принимается, чтобы быть неизмеренным воздействием. В общем случае _Tc, переменная, которой управляют, используемая, чтобы управлять реактором.

Линеаризовавшая модель соответствует общему формату пространства состояний

$\frac{d x}{d t} = A x + B u$

$y = C x + D u,$

где

$x = [\begin{matrix} {C^{'}}_{A} \\ T^{'} \end{matrix}], u = [\begin{matrix} {T^{'}}_{c} \\ {C^{'}}_{A i} \end{matrix}], y = [\begin{matrix} T^{'} \\ {C^{'}}_{A} \end{matrix}],$

$A = [\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}], B = [\begin{matrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{matrix}], C = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}], D = [\begin{matrix} 0 & 0 \\ 0 & 0 \end{matrix}]$

Следующий код показывает, как задать такую модель для некоторых определенных значений констант _bij и _aij:

A = [   -5  -0.3427; 
     47.68    2.785];
B = [    0   1
       0.3   0];
C = flipud(eye(2));
D = zeros(2);
CSTR = ss(A,B,C,D);

Эти значения соответствуют линеаризации вокруг рабочей точки, в которой _CA является 2 kmol/m³, T является 373 K, _CAf является 10 kmol/m³, _Tf является 300 K, и _Tc является 299 K. Смотрите, что Линеаризация Использует код MATLAB для получения дополнительной информации.

Можно задать вход, вывести и утвердить имена для модели CSTR. Кроме того, можно задать типы сигналов ввода и вывода.

CSTR.InputName = {'T_c', 'C_A_f'};  % set names of input signals
CSTR.OutputName = {'T', 'C_A'};     % set names of output signals
CSTR.StateName = {'C_A', 'T'};      % set names of state variables

% assign input and output signals to different MPC categories
CSTR=setmpcsignals(CSTR,'MV',1,'UD',2,'MO',1,'UO',2);

Здесь, MV, UD, MO, и UO поддержите "Переменную, которой Управляют", "Неизмеренное Воздействие", "Измеренный Выход", и "Неизмеренный Выход", соответственно.

Просмотрите модель CSTR и ее свойства.

CSTR

CSTR =
 
  A = 
            C_A        T
   C_A       -5  -0.3427
   T      47.68    2.785
 
  B = 
          T_c  C_A_f
   C_A      0      1
   T      0.3      0
 
  C = 
        C_A    T
   T      0    1
   C_A    1    0
 
  D = 
          T_c  C_A_f
   T        0      0
   C_A      0      0
 
Input groups:              
       Name        Channels
    Manipulated       1    
    Unmeasured        2    
                           
Output groups:            
       Name       Channels
     Measured        1    
    Unmeasured       2    
                          
Continuous-time state-space model.

Таким образом, в этой линеаризовавшей модели, первые переменные с двумя состояниями являются концентрацией реагента и температурой реактора, в то время как первые два входных параметров являются температурой хладагента и концентрацией реагента канала притока.

Для получения дополнительной информации о том, как получить эту линейную модель, смотрите, что эти два примера в Линеаризуют Модели Simulink. В первом примере линеаризация сделана в MATLAB^®, в то время как во втором это сделано с помощью Model Linearizer (Simulink Control Design) в Simulink.

Примеры с помощью модели CSTR

Следующие примеры используют линейную модель CSTR.

Создайте Линейные Независимые от времени Модели – Создают модели в пространстве состояний LTI для проекта MPC с помощью линейной модели CSTR.
Спроектируйте Контроллер Используя MPC Designer – Использование линейная модель CSTR, где реакторной температурой является измеренный выход. Используя MPC Designer, вы проектируете контроллер MPC, который стабилизирует с обратной связью при ограничении температуры хладагента CSTR и ее скорости изменения.
Спроектируйте Контроллер MPC в Командной строке – Проект тот же контроллер, спроектированный в предыдущем примере, но использовании инструкции MATLAB.
Протестируйте диспетчера MPC Робастнесса, использующего MPC Designer – Тест чувствительность вашего контроллера MPC к симуляциям ошибок предсказания в MPC Designer.
Вычислите Установившееся Усиление – Анализируют установившуюся эффективность контроллера MPC.
Сравните Несколько диспетчер Респонсес Используя MPC Designer – Сравнивают несколько ответов контроллера с помощью MPC Designer.

Следующие примеры используют нелинейную модель CSTR.

Пример Линеаризует Модели Simulink Используя MPC Designer, показывает, как линеаризовать нелинейную модель Simulink реактора в различных рабочих точках, и использующий разные подходы, в контексте разработки контроллера MPC, с помощью MPC Designer.

Точно так же в Проекте в качестве примера Контроллер MPC в Simulink, MPC Designer используется сначала, чтобы линеаризовать ту же нелинейную модель вокруг рабочей точки, в которой _CA вокруг 2 (kg · молекулярная масса)/m³ и затем спроектировать контроллер MPC для линеаризовавшего объекта. В этом примере _CA является единственный измеренный выход (и _Tc является входом управления).

Пример Симулирует Линейный Контроллер MPC с Нелинейным Объектом с помощью Последовательного использования Линеаризации for цикл, чтобы последовательно линеаризовать нелинейную модель с помощью linmod команда, перепроектируйте линейный контроллер MPC, вычислите вход управления и подайте его назад в нелинейную модель Simulink на каждом временном шаге. Этот подход больше не рекомендуется, используйте Адаптивный MPC или Запланированный на усиление MPC вместо этого.

Пример Адаптивное MPC управление Нелинейным Химическим Реактором Используя Последовательную Линеаризацию использует блок Adaptive MPC Controller, чтобы симулировать с обратной связью непосредственно в Simulink. Здесь блок линеаризации используется, чтобы извлечь линейную модель объекта управления из нелинейных уравнений на каждом временном шаге. В общем MPC адаптивное управление является предпочтительным подходом, когда линейная модель объекта управления может быть получена во время выполнения и когда все линеаризовавшие модели объекта управления имеют тот же порядок и задержку.

Точно так же в примере Адаптивное MPC управление Нелинейным Химическим Реактором Используя Онлайновую Оценку Модели Рекурсивное Средство оценки Полиномиальной модели используется (вместо блока линеаризации), чтобы идентифицировать 2D вход (_Tf и _Tc) и с одним выходом (T) ARX дискретного времени, основанный на модели на измеренных температурах в каждом контрольном интервале. Предполагаемая модель затем преобразуется в пространство состояний и питается блок Adaptive MPC Controller, который предоставляет вход управления нелинейному объекту. Онлайновая оценка может быть хорошим подходом, когда объект устойчив и медленно варьирование, и его уравнения не точно известны.

В примере Адаптивное MPC управление Нелинейным Химическим Реактором Используя Линейную Варьирующуюся по параметру Систему система линейного варьирования параметра (LPV), состоящая из трех линейных моделей объекта управления (в начальной букве, промежуточном звене и итоговой рабочей точке), создается оффлайн. Во время выполнения блок LPV System кормит соответствующей интерполяцией блок Adaptive MPC Controller, который предоставляет вход управления нелинейному объекту. Интерполяция объекта может быть хорошим подходом, когда в данной точке интерполированный объект является хорошим приближением фактического, переменная планирования варьируется сравнительно медленно, и получение линеаризовавшего объекта во время выполнения может быть слишком в вычислительном отношении дорогим или небезопасным.

В примере Запланированное на усиление MPC управление Нелинейным Химическим Реактором спроектированы три различных контроллера MPC (для объекта в начальной букве, промежуточном звене и итоговой рабочей точке). Эти контроллеры хранятся в блоке Multiple MPC Controllers и переключаются во время выполнения в соответствующих точках вдоль пути к переходу. Переключение контроллеров является хорошим подходом, когда линеаризовавшие модели объекта управления имеют различный порядок или задержки.

Наконец, в примере Нелинейное Прогнозирующее Управление Модели Экзотермического Химического Реактора, нелинейным объектом управляет один блок Nonlinear MPC Controller, с помощью _Tc в качестве входа управления и _CA как единственный измеренный выход. В общем случае нелинейное MPC управление является остающейся стратегией управлять очень нелинейными объектами, когда все предыдущие подходы являются неподходящими, или необходимо использовать нелинейные ограничения или неквадратичные функции стоимости.

Ссылки

[1] Bequette, B., Динамика Процесса: Моделирование, Анализ и Симуляция, Prentice Hall, 1998, Модуль 8, стр 641-660.

[2] Seborg, D. E. Т. Ф. Эдгар, и Д. А. Мелличамп, Динамика Процесса и Управление, 2-й Выпуск, Вайли, 2004, стр 34–36 и 94–95.

Смотрите также

setmpcsignals

Документация