Индуктор с неидеальным ядром
Simscape / Электрический / Пассивный элемент

Блок Nonlinear Inductor представляет индуктор неидеальным ядром. Ядро может быть неидеальным из-за его магнитных свойств и размерностей. Блок предоставляет следующие возможности параметризации:
Отношения между напряжением, текущим и потоком, заданы следующими уравнениями:
где:
v является терминальным напряжением.
i является терминальным током.
i L является током через индуктор.
G p является паразитной параллельной проводимостью.
N w является количеством обмотки поворотов.
Φ является магнитным потоком.
L является ненасыщенной индуктивностью.
Отношения между напряжением, текущим и потоком, заданы следующими уравнениями:
где:
v является терминальным напряжением.
i является терминальным током.
i L является током через индуктор.
G p является паразитной параллельной проводимостью.
N w является количеством обмотки поворотов.
Φ является магнитным потоком.
Смещение Φ является смещением насыщения магнитного потока.
L является ненасыщенной индуктивностью.
L находился, влажная индуктивность.
Отношения между напряжением, текущим и потоком, заданы следующими уравнениями:
где:
v является терминальным напряжением.
i является терминальным током.
i L является током через индуктор.
G p является паразитной параллельной проводимостью.
N w является количеством обмотки поворотов.
Φ является магнитным потоком.
Магнитный поток определяется одномерным поиском по таблице, на основе вектора из текущих значений и вектора из соответствующих значений магнитного потока, которые вы вводите. Можно создать эти векторы с помощью или отрицательных и положительных данных или положительных данных только. При использовании положительных данных только, вектор должен запуститься в 0, и отрицательные данные будут автоматически вычислены попеременно (приблизительно 0,0).
Отношения между напряжением, текущим и потоком, заданы следующими уравнениями:
где:
v является терминальным напряжением.
i является терминальным током.
i L является током через индуктор.
G p является паразитной параллельной проводимостью.
N w является количеством обмотки поворотов.
Φ является магнитным потоком.
B является плотностью магнитного потока.
H является силой магнитного поля.
l e является эффективной базовой длиной.
A e является эффективной базовой площадью поперечного сечения.
Плотность магнитного потока определяется одномерным поиском по таблице, на основе вектора из значений силы магнитного поля и вектора из соответствующих значений плотности магнитного потока, которые вы вводите. Можно создать эти векторы с помощью или отрицательных и положительных данных или положительных данных только. При использовании положительных данных только, вектор должен запуститься в 0, и отрицательные данные будут автоматически вычислены попеременно (приблизительно 0,0).
Отношения между напряжением, текущим и потоком, заданы следующими уравнениями:
где:
v является терминальным напряжением.
i является терминальным током.
i L является током через индуктор.
G p является паразитной параллельной проводимостью.
N w является количеством обмотки поворотов.
Φ является магнитным потоком.
B является плотностью магнитного потока.
μ 0 является магнитной константой, проницаемостью свободного пространства.
H является силой магнитного поля.
M является намагничиванием ядра индуктора.
l e является эффективной базовой длиной.
A e является эффективной базовой площадью поперечного сечения.
Действия намагничивания, чтобы повысить плотность магнитного потока и ее значение зависят и от текущего значения и от истории полевой силы H. Jiles-Атертон [1, 2] уравнения используются, чтобы определить M в любой момент времени. Рисунок ниже показывает типичный график получившегося отношения между B и H.
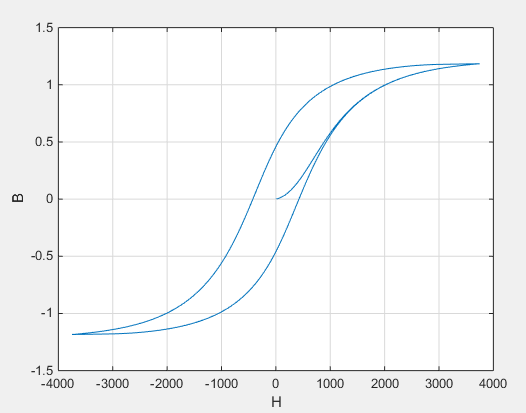
В этом случае намагничивание запускается как нуль, и следовательно график запускается в B = H = 0. Когда полевая сила увеличивается, график стремится к положительно идущей петле гистерезиса; затем на реверсировании скорость изменения H, это следует за отрицательно идущей петлей гистерезиса. Различие между положительно идущими и отрицательно идущими кривыми происходит из-за зависимости M на истории траектории. Физически поведение соответствует магнитным диполям в ядре, выравнивающемся, когда полевая сила увеличивается, но не затем полностью восстанавливающийся к их исходному положению, когда полевая сила уменьшается.
Начальная точка для уравнения Jiles-Атертона должна разделить эффект намагничивания в две части, та, которая является просто функцией эффективной полевой силы (эффективность H) и другой необратимая часть, которая зависит от прошлого:
M термин называется безгистерезисным намагничиванием, потому что это не показывает гистерезиса. Это описано следующей функцией текущего значения эффективной полевой силы, эффективности H:
Эта функция задает кривую насыщения с предельными значениями ±Ms и точка насыщения, определенного значением α, безгистерезисного масштабного фактора. Это может приблизительно считаться описанием среднего значения двух гистерезисных кривых. В блоке Nonlinear Inductor вы вводите значения для когда эффективность H = 0 и точка [H 1, B 1] на безгистерезисной кривой B-H, и они используются, чтобы определить значения для α и M s.
Параметр c является коэффициентом для обратимого намагничивания и диктует, сколько из поведения задано M и сколько необратимым термином M irr. Модель Jiles-Атертона задает необратимый термин частной производной относительно полевой силы:
Сравнение этого уравнения со стандартным дифференциальным уравнением первого порядка показывает, что, когда шаг в полевой силе, H, сделан, необратимый термин, из которого M irr пытается отследить обратимый термин M, но с переменным усилением отслеживания . Ошибка отслеживания действует, чтобы создать гистерезис в точках, где δ изменяет знак. Основным параметром, который формирует необратимую характеристику, является K, который называется bulk coupling coefficient. Параметр α называется inter-domain coupling factor и также используется, чтобы задать эффективную полевую силу, используемую при определении безгистерезисной кривой:
Значение α влияет на форму петли гистерезиса, большие значения, действующие, чтобы увеличить точки пересечения B-оси. Однако заметьте это для устойчивости термин должно быть положительным для δ> 0 и отрицательным для δ <0. Поэтому не все значения α допустимы, типичное максимальное значение, являющееся порядка 1e-3.
Можно определить представительные параметры для коэффициентов уравнения при помощи следующей процедуры:
Введите значение для параметра Anhysteretic B-H gradient when H is zero (когда эффективность H = 0) плюс точка данных [H 1, B 1] на безгистерезисной кривой B-H. От этих значений инициализация блока определяет значения для α и M s.
Установите параметр Coefficient for reversible magnetization, c, чтобы достигнуть правильного начального градиента B-H при запуске симуляции с [H B] = [0 0]. Значение c является приблизительно отношением этого начального градиента к Anhysteretic B-H gradient when H is zero. Значение c должно быть больше 0 и меньше чем 1.
Установите параметр Bulk coupling coefficient, K на аппроксимированную величину H когда B = 0 на положительно идущей петле гистерезиса.
Начните с очень маленького α, и постепенно увеличивайтесь, чтобы настроить значение B при пересечении H = 0 линий. Типичное значение находится в области значений 1e-4 к 1e-3. Значения, которые являются слишком большими, заставят градиент кривой B-H стремиться к бесконечности, которая является нефизической и генерирует ошибку утверждения во время выполнения.
Иногда необходимо выполнить итерации на этих четырех шагах, чтобы получить хорошее соответствие против предопределенной кривой B-H.
[1] Jiles, D. C. и Д. Л. Атэртон. “Теория ферромагнитного гистерезиса”. Журнал Магнетизма и Магнитных Материалов. Издание 61, 1986, стр 48–60.
[2] Jiles, D. C. и Д. Л. Атэртон. “Ферромагнитный гистерезис”. IEEE® Транзакции на Magnetics. Издание 19, № 5, 1983, стр 2183–2184.