stftmag2sig

Реконструкция сигнала от величины STFT

свернуть все на странице

Синтаксис

x = stftmag2sig(s,nfft)
x = stftmag2sig(s,nfft,fs)
x = stftmag2sig(s,nfft,ts)
x = stftmag2sig(___,Name,Value)
[x,t,info] = stftmag2sig(___)

Описание

пример

x = stftmag2sig(s,nfft) возвращает восстановленный временной интервал действительный сигнал, x, оцененный от величины Кратковременного преобразования Фурье (STFT), s, на основе алгоритма Гриффина-Лима. Функция принимает s был вычислен с помощью длины дискретного преобразования Фурье (ДПФ) nfft.

пример

x = stftmag2sig(s,nfft,fs) возвращает восстановленный сигнал, принимающий тот s был произведен на уровне fs.

x = stftmag2sig(s,nfft,ts) возвращает восстановленный сигнал, принимающий тот s был произведен с шагом расчета ts.

x = stftmag2sig(___,Name,Value) задает аргументы пары "имя-значение" использования дополнительных опций. Опции включают, среди других, окна FFT и метода, чтобы задать начальные фазы. Эти аргументы могут быть добавлены к любому из предыдущих входных синтаксисов. Например, 'FrequencyRange','onesided','InitializePhaseMethod','random' указывает, что сигнал восстановлен от одностороннего STFT со случайными начальными фазами.

[x,t,info] = stftmag2sig(___) также возвращает моменты времени, в которые сигнал восстановлен и структура, которая содержит информацию о процессе реконструкции.

Примеры

свернуть все

Скрипт Open Live Script

Рассмотрите 512 выборок синусоиды с нормированной частотой π/60 рад/отсчет и значение DC 1. Вычислите STFT сигнала.

n = 512;

x = cos(pi/60*(0:n-1)')+1;

S = stft(x);

Восстановите синусоиду от величины STFT. Постройте исходные и восстановленные сигналы.

xr = stftmag2sig(abs(S),size(S,1));

plot(x)
hold on
plot(xr,'--','LineWidth',2)
hold off
legend('Original','Reconstructed')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Reconstructed.

Повторите расчет, но теперь заполните сигнал нулями, чтобы уменьшить краевые эффекты.

xz = circshift([x; zeros(n,1)],n/2);

Sz = stft(xz);
xr = stftmag2sig(abs(Sz),size(Sz,1));

xz = xz(n/2+(1:n));
xr = xr(n/2+(1:n));

plot(xz)
hold on
plot(xr,'--','LineWidth',2)
hold off
legend('Original','Reconstructed')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Reconstructed.

Повторите расчет, но теперь уменьшите краевые эффекты путем принятия того x сегмент сигнала вдвое более долго.

xx = cos(pi/60*(-n/2:n/2+n-1)')+1;

Sx = stft(xx);
xr = stftmag2sig(abs(Sx),size(Sx,1));

xx = xx(n/2+(1:n));
xr = xr(n/2+(1:n));

plot(xx)
hold on
plot(xr,'--','LineWidth',2)
hold off
legend('Original','Reconstructed')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Reconstructed.

Скрипт Open Live Script

Загрузите звуковой сигнал, который содержит два уменьшающихся щебета, и широкополосное обрызгивают звук. Сигнал производится на уровне 8 192 Гц. Постройте STFT сигнала. Разделите форму волны на сегменты с 128 выборками и окно сегменты с помощью Окна Хэмминга. Задайте 64 выборки перекрытия между смежными сегментами и точками БПФ 10:24.

load splat
ty = (0:length(y)-1)/Fs;

% To hear, type sound(y,Fs)

wind = hamming(128);
olen = 64;
nfft = 1024;

stft(y,Fs,'Window',wind,'OverlapLength',olen,'FFTLength',nfft)

Figure contains an axes object. The axes object with title Short-Time Fourier Transform contains an object of type image.

Вычислите величину и фазу STFT.

s = stft(y,Fs,'Window',wind,'OverlapLength',olen,'FFTLength',nfft);

smag = abs(s);
sphs = angle(s);

Восстановите сигнал на основе величины STFT. Используйте те же параметры, что вы использовались для расчета STFT. По умолчанию, stftmag2sig инициализирует фазы, чтобы обнулить и использует 100 итераций оптимизации.

[x,tx,info] = stftmag2sig(smag,nfft,Fs,'Window',wind,'OverlapLength',olen);

% To hear, type sound(x,Fs)

Постройте исходные и восстановленные сигналы. Для лучшего сравнения, смещение восстановленный сигнал и направо.

plot(ty,y,tx+500/Fs,x+1)
legend('Original','Reconstructed','Location','best')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Reconstructed.

Выведите относительное улучшение к сходимости между последними двумя итерациями.

impr = info.Inconsistency
impr = 0.0424

Улучшите реконструкцию путем удвоения количества итераций оптимизации и установки начальных фаз на фактические фазы от STFT. Постройте исходные и восстановленные сигналы. Для лучшего сравнения постройте отрицание восстановленного сигнала и возместите его и направо.

[x,tx,info] = stftmag2sig(smag,nfft,Fs,'Window',wind,'OverlapLength',olen, ...
    'MaxIterations',200,'InitialPhase',sphs);

% To hear, type sound(x,Fs)

plot(ty,y,tx+500/Fs,-x+1)
legend('Original','Reconstructed','Location','best')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Reconstructed.

Выведите относительное улучшение к сходимости между последними двумя итерациями.

impr = info.Inconsistency
impr = 1.3874e-16

Входные параметры

свернуть все

Величина STFT в виде матрицы. s должен соответствовать одноканальному, вещественному сигналу.

Пример: abs(stft(sin(пи/2* (0:255)), 'FFTLength', 128)) задает величину STFT синусоиды.

Пример: abs(stft(chirp(0:1/1e3:1,25,1,50))) задает величину STFT щебета, произведенного на уровне 1 кГц.

Типы данных: single | double

Количество ДПФ указывает в виде положительного целочисленного скаляра. Этот аргумент всегда требуется.

Типы данных: single | double

Частота дискретизации в виде положительного числового скаляра.

Шаг расчета в виде a duration скаляр. Определение ts эквивалентно установке частоты дискретизации f s = 1/ts.

Пример: seconds(1) isa duration скаляр, представляющий различие с 1 вторым разом между последовательными выборками сигнала.

Типы данных: duration

Аргументы name-value

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'FrequencyRange','onesided','InitializePhaseMethod','random' указывает, что сигнал восстановлен от одностороннего STFT со случайными начальными фазами.

Параметр отображения несоответствия в виде разделенной запятой пары, состоящей из 'Display' и логическое значение. Если эта опция установлена в trueто stftmag2sig отображает нормированное несоответствие после каждых 20 итераций оптимизации, и оно также отображает останавливающуюся информацию в конце запуска.

Типы данных: логический

Частотный диапазон величины STFT в виде разделенной запятой пары, состоящей из 'FrequencyRange' и 'centered', 'twosided', или 'onesided'.

  • 'centered' — Обработайте s как величина двухстороннего, сосредоточенного STFT. Если nfft является четным, затем s взят, чтобы быть вычисленными на интервале (–π, π] рад/отсчет. Если nfft является нечетным, затем s взят, чтобы быть вычисленными на интервале (–π, π) рад/отсчет. Если вы указываете информацию времени, то интервалы (–fs, f s/2] циклы/единица времени и (–fs, f s/2) циклы/единица времени, соответственно, где f s является частотой дискретизации.

  • 'twosided' — Обработайте s как величина двухстороннего STFT, вычисленного на интервале [0, 2π) рад/отсчет. Если вы указываете информацию времени, то интервал [0, f s), циклы/единица времени.

  • 'onesided' — Обработайте s как величина одностороннего STFT. Если nfft является четным, затем s взят, чтобы быть вычисленными на интервале [0, π] рад/отсчет. Если nfft является нечетным, затем s взят, чтобы быть вычисленными на интервале [0, π), рад/отсчет. Если вы указываете информацию времени, то интервалы являются [0, f s/2] циклами/единицей времени и [0, f s/2), циклы/единица времени, соответственно, где f s является частотой дискретизации.

Типы данных: char | string

Допуск несоответствия процесса реконструкции в виде разделенной запятой пары, состоящей из 'InconsistencyTolerance' и положительная скалярная величина. Процесс реконструкции останавливается, когда Нормированное Несоответствие ниже, чем допуск.

Типы данных: single | double

Инициализация фазы в виде разделенной запятой пары, состоящей из 'InitializePhaseMethod' и 'zeros' или 'random'. Задайте только один из 'InitializePhaseMethod' или 'InitialPhase'.

  • 'zeros' — Функция инициализирует фазы как нули.

  • 'random' — Функция инициализирует фазы как случайные числа, распределенные однородно в интервале [–π, π].

Типы данных: char | string

Начальные фазы в виде разделенной запятой пары, состоящей из 'InitialPhase' и действительная числовая матрица в области значений [–π, π]. Матрица должна иметь тот же размер как s. Задайте только один из 'InitializePhaseMethod' или 'InitialPhase'.

Пример: \anglestft(randn(1000,1))) задает фазы кратковременного преобразования Фурье случайного сигнала.

Пример: 2*pi*(rand(size(stft(randn(1000,1))))-1/2) задает матрицу случайных фаз, распределенных однородно в интервале [–π, π]. Матрица имеет тот же размер как кратковременное преобразование Фурье случайного сигнала.

.

Типы данных: single | double

Введите измерение времени в виде разделенной запятой пары, состоящей из 'InputTimeDimension' и 'acrosscolumns' или 'downrows'.

  • 'acrosscolumns' — Функция принимает что измерение времени s через столбцы, и размерность частоты снижается на строки.

  • 'downrows' — Функция принимает что измерение времени s снижается на строки, и размерность частоты через столбцы.

Типы данных: char | string

Максимальное количество итераций оптимизации в виде разделенной запятой пары, состоящей из 'MaxIterations' и положительный целочисленный скаляр. Процесс реконструкции останавливается, когда количество итераций больше 'MaxIterations'.

Типы данных: single | double

Алгоритм реконструкции сигнала в виде разделенной запятой пары, состоящей из 'Method' и один из них:

  • 'gla' — Исходный алгоритм реконструкции, предложенный Гриффином и Лимом и, описал в [1].

  • 'fgla' — Быстрый алгоритм Гриффина-Лима, предложенный Perraudin, Balazs и Søndergaard и, описал в [2].

  • 'legla' — Алгоритм FAST, предложенный Ле Ру, Kameoka, Оно и Сэгаямой и, описал в [3].

Типы данных: char | string

Количество перекрытых выборок между смежными сегментами в виде разделенной запятой пары, состоящей из 'OverlapLength' и положительное целое число, меньшее, чем длина 'Window'. Успешная реконструкция сигнала требует 'OverlapLength' совпадать с количеством перекрытых сегментов раньше генерировало величину STFT. Если вы не используете 'OverlapLength' или задайте его как пустой, это установлено в самое большое целое число, меньше чем или равное 75% длины окна, которая является 96 выборками для окна Hann по умолчанию.

Типы данных: double | single

Порядок усечения для 'legla' обновите правило в виде разделенной запятой пары, состоящей из 'TruncationOrder' и положительное целое число. Этот аргумент применяется только когда 'Method' установлен в 'legla' и управляет количеством значений фазы, обновленных в каждой итерации того метода. Если не заданный, 'TruncationOrder' определяется с помощью адаптивного алгоритма.

Типы данных: single | double

Обновите параметр для быстрого алгоритма Гриффина-Лима в виде разделенной запятой пары, состоящей из 'UpdateParameter' и положительная скалярная величина. Этот аргумент применяется только когда 'Method' установлен в 'fgla' и задает параметр для правила обновления того метода.

Типы данных: single | double
Поддержка комплексного числа: Да

Спектральное окно в виде разделенной запятой пары, состоящей из 'Window' и вектор. Успешная реконструкция сигнала требует 'Window' совпадать с окном раньше генерировало величину STFT. Если вы не задаете окно или задаете его как пустой, функция использует периодическое окно Hann длины 128. Длина 'Window' должен быть больше или быть равен 2.

Для списка доступных окон смотрите Windows.

Пример: hann(128,'periodic') и (1-cos(2*pi*(128:-1:1)'/128))/2 оба задают окно по умолчанию, используемое stftmag2sig.

Типы данных: double | single

Выходные аргументы

свернуть все

Восстановленный сигнал временной области, возвращенный как вектор.

Моменты времени, в которые восстановлен сигнал, возвратились как вектор.

Информация о процессе реконструкции, возвращенная как структура, содержащая эти поля:

  • ExitFlag — Флаг Termination.

    • Значение 0 указывает на алгоритм, остановленный, когда он достиг максимального количества итераций.

    • Значение 1 указывает на алгоритм, остановленный, когда он соответствовал относительной погрешности.

  • NumIterations — Общее количество итераций.

  • Inconsistency — Среднее относительное улучшение к сходимости между последними двумя итерациями.

  • ReconstructedPhase — Восстановленная фаза в последней итерации.

  • ReconstructedSTFT — Восстановленное кратковременное преобразование Фурье в последней итерации.

Больше о

свернуть все

Кратковременное преобразование Фурье

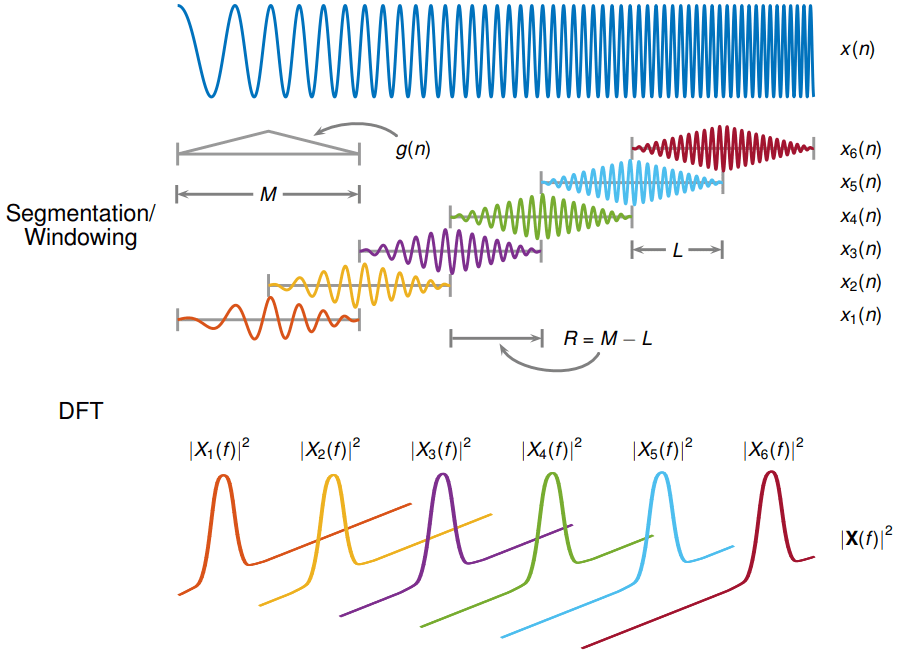
Кратковременное преобразование Фурье (STFT) используется, чтобы анализировать, как содержимое частоты неустановившегося сигнала изменяется в зависимости от времени.

STFT сигнала вычисляется путем скольжения analysis window длины M по сигналу и вычислению дискретного преобразования Фурье оконных данных. Окно скачкообразно двигается по исходному сигналу с промежутками в R выборки. Функции окна Most сужаются в ребрах, чтобы избежать спектрального вызова. Если ненулевая длина перекрытия L задан, добавление перекрытия, которое оконные сегменты компенсируют затухание сигнала в ребрах окна. ДПФ каждого оконного сегмента добавляется к матрице, которая содержит величину и фазу для каждого момента времени и частоты. Количеством столбцов в матрице STFT дают

k=⌊Nx−LM−L⌋,

где Nx длина исходного сигнала x(n) и ⌊⌋ символы обозначают функцию пола. Количество строк в матрице равняется ДПФ N, количеству точек ДПФ, для и двухсторонних преобразований в центре и ⌊NDFT/2 ⌋ + 1 для односторонних преобразований.

Матрицей STFT дают X(f)=[X1(f)X2(f)X3(f)⋯Xk(f)] таким образом, что mэлемент th этой матрицы

Xm(f)=∑n=−∞∞x(n)g(n−mR)e−j2πfn,

где

  • g(n) — Функция окна длины M.

  • Xm(f) — ДПФ оконных данных сосредоточен во время mR.

  • R — Скачкообразно переместите размер между последовательными ДПФ, размер транзитного участка является различием между длиной окна Mи длина перекрытия L.

Величина, в квадрате из STFT, уступает spectrogram представление спектральной плотности мощности функции.

Нормированное несоответствие

normalized inconsistency измеряет улучшение к сходимости процесса реконструкции в последовательных итерациях оптимизации.

Нормированное несоответствие задано как

Inconsistency=‖STFT(ISTFT(sest))−sest‖‖sest‖,

где оценка s является комплексным кратковременным преобразованием Фурье, оцененным в каждой итерации, скобки обозначают матричную норму, STFT обозначает кратковременное преобразование Фурье, и ISTFT обозначает свою инверсию. stftmag2sig использует MATLAB® функция norm вычислить матричные нормы. Для получения дополнительной информации о STFT и его инверсии, смотрите Кратковременное преобразование Фурье и Обратное Кратковременное преобразование Фурье.

Ссылки

[1] Гриффин, Дэниел В. и Джэ С. Лим. "Оценка сигнала от Модифицированного Кратковременного преобразования Фурье". Транзакции IEEE на Акустике, Речи и Обработке сигналов. Издание 32, Номер 2, апрель 1984, стр 236–243. https://doi.org/10.1109/TASSP.1984.1164317.

[2] Perraudin, Nathanaël, Питер Бэлэзс и Питер Л. Сындергэард. "Быстрый Алгоритм Гриффина-Лима". В 2 013 Семинарах IEEE по Приложениям Обработки сигналов к Аудио и Акустике, Нью-Пальтцу, Нью-Йорк, 20-23 октября 2013. https://doi.org/10.1109/WASPAA.2013.6701851.

[3] Ле Ру, Джонатан, Hirokazu Kameoka, Нобутэка Оно и Шиджеки Сэгаяма. "Быстрая Реконструкция Сигнала от Величины Спектрограмма STFT На основе Непротиворечивости Спектрограммы". В Продолжениях 13-й Международной конференции по вопросам Эффектов Цифрового аудио (DAFx-10), Граца, Австрия, 6-10 сентября 2010.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Функции

Введенный в R2020b

Документация Signal Processing Toolbox

Поддержка

Для просмотра документации необходимо авторизоваться на сайте