Используйте дифференциальные уравнения, кинетику действующих масс или кинетику Михаэлиса-Ментен, для определения ферментативных реакций.
Простая модель для катализируемых ферментом реакций запускает подложку S обратимо связывая с ферментом E. Часть подложки в комплексе подложки/фермента преобразована в продукт P с релизом фермента.
Эта простая модель может быть задана с
Дифференциальные уравнения скорости. Смотрите Ферментативные реакции с Дифференциальными Уравнениями скорости.
Реакции с кинетикой действующих масс. Смотрите Ферментативные реакции с Кинетикой действующих масс.
Реакции с кинетикой Генри-Михаэлиса-Ментен. Смотрите Ферментативные реакции с Необратимой кинетикой Генри-Михаэлиса-Ментен.
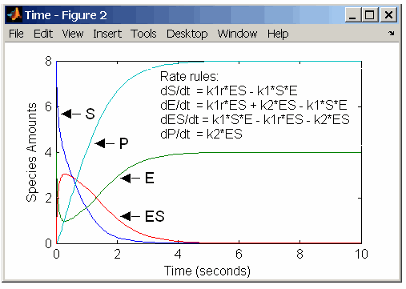
Реакции для механизма ферментативной реакции с одним субстратом (см. Простую Модель для Одно-субстратных катализируемых реакций) могут быть описаны с дифференциальными уравнениями скорости. Вы можете ввести дифференциальные уравнения скорости в программное обеспечение в качестве правила скоростей.
reactions: none
reaction rate: none
rate rules: dS/dt = k1r*ES - k1*S*E
dE/dt = k1r*ES + k2*ES - k1*S*E
dES/dt = k1*S*E - k1r*ES - k2*ES
dP/dt = k2*ES
species: S = 8 mole
E = 4 mole
ES = 0 mole
P = 0 mole
parameters: k1 = 2 1/(mole*second)
k1r = 1 1/second
k2 = 1.5 1/secondПомните что правило скорости dS/dt = f(x) написан в SimBiology® выражение правила скорости как S = f(x). Для получения дополнительной информации о правилах скоростей смотрите Правила скоростей.
В качестве альтернативы вы могли удалить правило скорости для ES, добавьте новую разновидность Etotal для общей суммы фермента, и добавляют алгебраическое правило 0 = Etotal - E - ES, где начальная буква составляет для Etotal и E равны.
reactions: none
reaction rate: none
rate rules: dS/dt = k1r*ES - k1*S*E
dE/dt = k1r*ES + k2*ES - k1*S*E
dP/dt = k2*ES
algebraic rule: 0 = Etotal - E - ES
species: S = 8 mole
E = 4 mole
ES = 0 mole
P = 0 mole
Etotal = 4 mole
parameters: k1 = 2 1/(mole*second)
k1r = 1 1/second
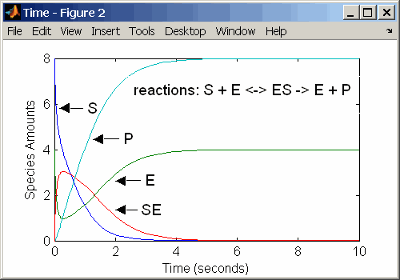
k2 = 1.5 1/secondОпределение дифференциальных уравнений скорости для реакций в модели является длительным процессом. Лучший путь состоит в том, чтобы ввести реакции для одно-субстратного механизма ферментативной реакции непосредственно в программное обеспечение. Следующее использование в качестве примера моделирует катализируемую ферментом реакцию с кинетикой действующих масс. Для описания модели реакции см. Простую Модель для Одно-субстратных катализируемых реакций.
reaction: S + E -> ES
reaction rate: k1*S*E (binding)
reaction: ES -> S + E
reaction rate: k1r*ES (unbinding)
reaction: ES -> E + P
reaction rate: k2*ES (transformation)
species: S = 8 mole
E = 4 mole
ES = 0 mole
P = 0 mole
parameters: k1 = 2 1/(mole*second)
k1r = 1 1/second
k2 = 1.5 1/secondРезультаты для симуляции с помощью реакций идентичны результатам использования дифференциальных уравнений скорости.
Представление катализируемой ферментом реакции с кинетикой действующих масс требует, чтобы вы знали константы скорости k1, k1r, и k2. Однако об этих константах скорости редко сообщают в литературе. Более распространено дать константы скорости для кинетики Генри-Михаэлиса-Ментен с максимальной скоростью Vm=k2*E и постоянный Km = (k1r + k2)/k1. Скорость реакции для одно-субстратной ферментативной реакции с помощью кинетики Генри-Михаэлиса-Ментен приведена ниже. Для получения информации о модели см. Простую Модель для Одно-субстратных катализируемых реакций.
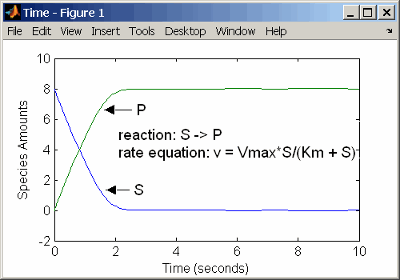
Следующий пример демонстрирует катализируемую ферментом реакцию с помощью кинетики Генри-Михаэлиса-Ментен с одной реакцией и уравнением скорости реакции. Введите реакцию, заданную ниже в программное обеспечение, и симулируйте.
reaction: S -> P
reaction rate: Vmax*S/(Km + S)
species: S = 8 mole
P = 0 mole
parameters: Vmax = 6 mole/second
Km = 1.25 moleРезультаты показывают график, немного отличающийся из графика с помощью кинетики действующих масс. Различия происходят из-за предположений, сделанных при получении уравнения скорости Михаэлиса-Ментен.