Альберт Голдбетер изменил модель с каскадами фермента [Голдбетер и Koshland 1981], чтобы соответствовать данным о клеточном цикле из исследований с эмбриональными ячейками [Goldbeter 1991]. Он использовал эту модель, чтобы продемонстрировать пороги с каскадами фермента и периодическим поведением, вызванным отрицательной обратной связью.
Существует два SimBiology® изменения модели с помощью модели Голдбетера. Первая модель использует дифференциальные уравнения скорости непосредственно из статьи Голдбетера. Вторая модель создана с реакциями с помощью кинетики Генри-Михаэлиса-Ментен.
Альберт Голдбетер создал простую модель клеточного деления из исследований с эмбриональными ячейками [Goldbeter 1991]. Эта модель демонстрирует пороги с каскадами фермента и периодическим поведением, вызванным отрицательной обратной связью.
Существует шесть разновидностей в минимальной митотической модели генератора Голдбетера [Goldbeter 1991].
C Циклин. Периодическое поведение циклина активирует и деактивировало каскад фермента.
M +, M — Неактивный (phosphorylated) и активные формы cdc2 киназы. Киназы катализируют сложение групп фосфата на остатки аминокислоты.
X +, X — Неактивный и активный (phosphorylated) формы протеазы циклина. Протеазы ухудшают белки путем разрывания связей пептида.
Реакции помечены r1 к r7 на следующей схеме.
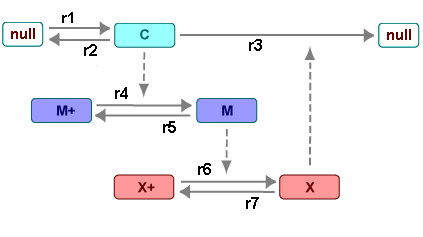
Эта модель показывает:
Как пороги с cdc2 активацией киназы (M +-> M) и активацией протеазы (X +-> X) может произойти как результат ковалентной модификации (например, фосфорилирование или dephosphorylation), но без потребности в положительной обратной связи.
Как периодическое поведение с cdc2 активацией киназы может произойти с отрицательной обратной связью и задержкой, сопоставленной с каскадами фермента активации/деактивации.
Следующий список описывает каждую из реакций в минимальном митотическом генераторе Голдбетера с некоторыми предположениями упрощения. Для более подробного объяснения модели смотрите [Goldbeter 1991].
Циклин (C) синтезируется на постоянном уровне (r1) и ухудшается на постоянном уровне (r2).
Циклин (C) не объединяет с cdc2 киназой (M).
Циклин (C) активирует cdc2 киназу (M +-> M) путем увеличения скорости фосфатазы, которая активирует киназу. Неактивная cdc2 киназа (M+) активируется путем удаления запрещения групп фосфата (r4).
Объем деактивации киназы (не смоделированный) для cdc2 киназы (M) является постоянным. Активная cdc2 киназа (M) деактивирована путем добавления запрещения группы (r5) фосфата.
Активация протеазы циклина (X+ -> X) активной cdc2 киназой (M) является прямым без других прошедших каскадов. Протеаза циклина (X) активируется путем добавления групп фосфата (r6).
Объем деактивации фосфатазы (не смоделированный) для протеазы циклина (X) является постоянным. Активная протеаза циклина (X) деактивирован путем удаления активирующихся групп фосфата (r7).
Три разновидности интереса являются циклином (C), активная киназа dephosphorylated cdc2 (M), и активная phosphorylated протеаза (X). Общие суммы (M + M+) и (X + X+) являются постоянными.
Минимальная митотическая модель генератора Голдбетера задана с тремя дифференциальными уравнениями скорости и двумя алгебраическими уравнениями, которые задают изменяющиеся параметры в уравнениях скорости.
Дифференциальное Уравнение скорости 1, Циклин (C). Следующее дифференциальное уравнение скорости от [Goldbeter 1991] для циклина (C).
Дифференциальное Уравнение скорости 2, Киназа (M). Следующее дифференциальное уравнение скорости для cdc2 киназы (M). Заметьте, что (1 - M) сумма неактивных (phosphorylated) cdc2 киназа (M+).
Уравнение скорости 3 Дифферентиэла, уравнения скорости Протиса (кс). Дифферентиэла для протеазы циклина (X). Заметьте, что (1 - X) сумма неактивной (unphosphorylated) протеазы циклина (X+).
В литературе много биологических моделей заданы с помощью дифференциального уровня и алгебраических уравнений. С программным обеспечением SimBiology можно ввести уравнения непосредственно, когда SBML управляет. Пример в этом разделе использует митотический генератор Голдбетера, чтобы проиллюстрировать этот тезис.
Запись дифференциальных уравнений скорости в однозначном формате, который может изучить программа, является довольно простым процессом.
Используйте звездочку, чтобы указать на умножение. Например, k[a] записанный k*a.
Удалите квадратные скобки, которые указывают на концентрацию со всех разновидностей. Модули, сопоставленные с разновидностями, укажут на концентрацию (moles/liter) или сумма (moles, molecules).
Программное обеспечение SimBiology использует квадратные скобки вокруг разновидностей и названия параметра, чтобы позволить имена, которые не являются допустимым MATLAB® имена переменных. Например, у вас могла быть разновидность под названием glucose-6-phosphate dehydrogenase но необходимо добавить скобки вокруг имени в уравнениях правила и скорости реакции.
Используйте круглые скобки, чтобы разъяснить порядок оценки для математических операций. Например, не пишите уровень Henri-Михаэлиса-Ментен как Vm*C/Kd + C, потому что Vm*C разделен на Kd прежде, чем добавить C, и затем C добавляется к результату.
Следующее уравнение является правилом скорости для Дифференциального Уравнения скорости 1, Циклин (C):
dC/dt = vi - (vd*X*C)/(Kd + C) - kd*C
Следующие уравнения являются уровнем и repeatedAssignment правила для Дифференциального Уравнения скорости 2, Киназа (M):
dM/dt = (V1*Mplus)/(K1 + Mplus) - (V2*M)/(K2 + M) V1 = (VM1*C)/(Kc + C) Mplus = Mt - M
Следующие уравнения являются уровнем и repeatedAssignment правила для Дифференциального Уравнения скорости 3, Протеаза (X):
dX/dt = (V3*Xplus)/(K3 + Xplus) - (V4*X)/(K4 + X) V3 = VM3*M Xplus = Xt - X
Правила. Активное (M) и неактивный (Mplus) формы киназы приняты, чтобы быть частью сохраненного цикла с общей концентрацией (Mt) оставление постоянного во время симуляции. Вам нужно только одно дифференциальное уравнение скорости массовым уравнением баланса, чтобы задать суммы обеих разновидностей. Точно так же активное (X) и неактивный (Xplus) формы протеазы являются частью второго сохраненного цикла.
Это - симуляция минимального митотического генератора Голдбетера с помощью дифференциального уровня и алгебраических уравнений. Симулируйте с sundials решатель и разновидности C графикаM, и X. Для описания модели см. Модель SimBiology с Правилами.
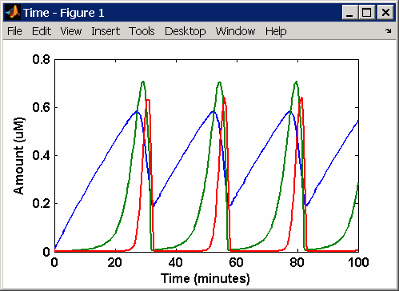
В литературе много моделей заданы с дифференциальными уравнениями скорости. С программным обеспечением SimBiology создание дифференциальных уравнений от реакций является ненужным; можно ввести реакции и позволить программному обеспечению вычислить уравнения.
Некоторые модели заданы с дифференциальными уравнениями скорости, и вам могут быть нужны реакции быть совместимыми с вашей моделью. Два правила, которые можно использовать, чтобы преобразовать дифференциальные уравнения скорости в реакции:
Для положительного термина — разновидность, описанная уравнением, помещается справа как продукт, и разновидности в термине помещаются слева как реагенты.
Для отрицательного термина — разновидность, описанная уравнением, помещается слева как продукт, и разновидности в термине также помещаются слева как реагенты.
Необходимо определить продукты с помощью дополнительной информации, например, схемы реакции, описания модели или понимания реакции. Если реакция катализируется киназой, то можно прийти к заключению, что продукт имеет одну или несколько дополнительных групп фосфата.
Простая реакция первого порядка имеет дифференциальное уравнение скорости dR/dt = +kr[P] - kf[R]. Отрицательный термин подразумевает, что реакцией является R -> ? с неизвестным продуктом. Положительный термин идентифицирует продукт и завершает реакцию, R <-> P.
Реакции R1 к R3 от уравнения E1. Дифференциальное уравнение скорости 1 повторяется здесь для сравнения с реакциями. См. Дифференциальное Уравнение скорости 1, Циклин (C).
Реакция и уравнения скорости реакции из дифференциального уравнения скорости E1 приведены ниже:
r1 reaction: null -> C reaction rate: vi r2 reaction: C -> null reaction rate: kd*C r3 reaction: C -> null reaction rate: (vd*X*C)/(Kd + C)
Реакции R4 и R5 от уравнения E2. Дифференциальное уравнение скорости 2 и алгебраическое уравнение 2 повторяются здесь для сравнения с реакциями. См. Дифференциальное Уравнение скорости 2, Киназа (M).
Реакция и уравнения скорости реакции из дифференциального уравнения скорости E2 приведены ниже:
r4 reaction: Mplus -> M
reaction rate: V1*Mplus/(K1 + Mplus)
repeatedAssignment rule: V1 = VM1*C/(Kc + C)
r5 reaction: M -> Mplus
reaction rate: V2*M/(K2 + M)Реакции R6 и R7 от уравнения E3. Дифференциальное уравнение скорости для уравнения 3 и алгебраического уравнения 3 повторяется здесь для сравнения с реакциями.
V3 = VM3*[M]
Реакция и уравнения скорости реакции из дифференциального уравнения скорости E3 приведены ниже:
r6 reaction: Xplus -> X
reaction rate: V3*Xplus]/(K3 + Xplus)
repeatedAssignment rule: V3 = VM3*M
r7 reaction: X -> Xplus
reaction rate: V4*X/(K4 + X)После того, как вы преобразовали дифференциальные уравнения скорости в реакции и уравнения скорости реакции, можно начать заполнять начальные значения для разновидностей (реагенты и продукты) и параметры.
Начальные значения для параметров и суммы для разновидностей перечислены с четырьмя различными модулями в той же размерности:
A — Исходные модули в газете Goldbeter 1991.
B Модули концентрации со временем, преобразованным во второй. При преобразовании к b, используйте 1 minute = 60 second для параметров.
C Модули суммы как родинки. При преобразовании концентрации в родинки используйте объем ячейки 1e-12 литр и принимает, что объем не изменяется.
D Модули суммы как молекулы. При преобразовании суммы как родинок к молекулам используйте 6.022e23 molecules = 1 mole.
С размерным анализом и модульным преобразованием прочь, выберите все модули для одной буквы. Например, выберите весь из Как. Если размерный анализ и модульное преобразование включены, вы можете буквы смешивания и подгонки и получать тот же ответ.
Реакция 1 синтез циклина
| R1 | Значение | Модули | |
|---|---|---|---|
| реакция | пустой указатель-> C | ---- | ---- |
| скорость реакции | vi | ---- | A. гм/минута |
| ---- | B. родинка / (liter*second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
| параметры | vi | 0.025 | A. гм/минута |
| 4.167e-10 | B. родинка / (liter*second) | ||
| 4.167e-22 | C. родинка/секунда | ||
| 205 | D. молекула/секунда | ||
| разновидности | C | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Реакция 2 циклина недифференцируемое ухудшение
| R2 | Значение | Модули | |
|---|---|---|---|
| реакция | C -> null | ---- | ---- |
| скорость реакции | kd*C | ---- | A. гм/минута |
| ---- | B. родинка / (liter*second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
| параметры | kd | 0.010 | A. 1/минута |
| 1.6667e-4 | B, C, D. 1/второй | ||
| разновидности | C | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Реакция 3 ухудшения протеазы циклина
| R3 | Значение | Модули | |
|---|---|---|---|
| реакция | C -> null | ---- | ---- |
| скорость реакции | (vd*X*C)/(Kd + C) | ---- | A. гм/минута |
| ---- | B. родинка / (liter*second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
| параметр | vd | 0.25 | A. 1/минута |
| 0.0042 | B, C, D. 1/второй | ||
| параметр | Kd | 0.02 | A. гм |
| 2.0e-8 | B. родинка/литр | ||
| 2.0e-020 | C. родинка | ||
| 12044 | D. молекула | ||
| разновидности | C (подложка) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула | ||
| разновидности | X (фермент) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Реакция 4 активации киназы Cdc2
| R4 | Значение | Модули | |
|---|---|---|---|
| реакция | Mplus -> M | ---- | ---- |
| скорость реакции | (V1*Mplus)/(K1 + Mplus) | ---- | A. гм/минута |
| ---- | B. родинка / (liter*second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
repeatedAssignment правило | V1 = (VM1*C)/(Kc + C) | ---- | |
| параметр | V1 (переменная по правилу) | 0.00 | A. гм/минута B. родинка / (liter*second) C. родинка/секунда D. молекула/секунда |
| параметр | VM1 | 3.0 | A. гм/минута |
| 5.0e-8 | B. родинка / (liter*second) | ||
| 5.0000e-020 | C. родинка/секунда | ||
| 30110 | D. молекула/секунда | ||
| параметр | Kc | 0.5 | A. гм |
| 5.0000e-7 | B. родинка/литр | ||
| 5.0e-19 | C. родинка | ||
| 3.011e+5 | D. молекула | ||
| параметр | K1 | 0.005 | A. гм |
| 5e-9 | B. родинка/литр | ||
| 5e-21 | C. родинка | ||
| 3.011e+3 | D. молекула | ||
| разновидности | Mplus (неактивная подложка) | 0.99 | A. гм |
| 9.9e-7 | B. родинка/литр | ||
| 9.9e-19 | C. родинка | ||
| 5.962e+5 | D. молекула | ||
| разновидности | M (активный продукт) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула | ||
| разновидности | C | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Реакция 5 деактиваций киназы Cdc2
| R5 | Значение | Модули | |
|---|---|---|---|
| реакция | M -> M_plus | ---- | ---- |
| скорость реакции | (V2*M)/(K2 + M) | ---- | A. гм/минута |
| ---- | B. (mole/liter-second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
| параметр | V2 | 1.5 | A. гм/минута |
| 2.5000e-008 | B. mole/liter-second | ||
| 2.5000e-020 | C. родинка/секунда | ||
| 15055 | D. молекула/секунда | ||
| параметр | K2 | 0.005 | A. гм |
| 5.0000e-009 | B. родинка/литр | ||
| 5.0000e-021 | C. родинка | ||
| 3011 | D. молекула | ||
| 1.0e-20 | C. родинка | ||
| разновидности | Mplus (неактивный) | 0.99 | A. гм |
| 9.9e-7 | B. родинка/литр | ||
| 9.9e-19 | C. родинка | ||
| 5.962e+5 | D. молекула | ||
| разновидности | M (активный) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Реакция 6 активаций протеазы
| R6 | Значение | Модули | |
|---|---|---|---|
| реакция | Xplus -> X | ---- | ---- |
| скорость реакции | (V3*Xplus)/(K3 + Xplus) | ---- | A. гм/минута |
| ---- | B. родинка / (liter*second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
repeatedAssignment правило | V3 = VM3*M | ---- | |
| параметр | V3 (переменная по правилу) | A. гм/минута B. mole/liter-second C. родинка/секунда D. молекула/секунда | |
| параметр | VM3 | 1.0 | A. 1/минута |
| 0.0167 | B, C, D. 1/второй | ||
| параметр | K3 | 0.005 | A. гм |
| 5e-9 | B. родинка/литр | ||
| 5e-21 | C. родинка | ||
| 3.011e+3 | D. молекула | ||
| разновидности | Xplus (неактивная подложка) | 0.99 | A. гм |
| 9.9e-7 | B. родинка/литр | ||
| 9.9e-19 | C. родинка | ||
| 5.962e+5 | D. молекула | ||
| разновидности | X (активный продукт) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула | ||
| разновидности | M (фермент) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Реакция 7 деактиваций протеазы
| R7 | Значение | Модули | |
|---|---|---|---|
| реакция | X -> X_plus | ---- | ---- |
| скорость реакции | (V4*X)/(K4 + X) | ---- | A. гм/минута |
| ---- | B. родинка / (liter*second) | ||
| ---- | C. родинка/секунда | ||
| ---- | D. молекула/секунда | ||
| параметр | V4 | 0.5 | A. гм/минута |
| 8.3333e-009 | B. родинка / (liter*second) | ||
| 8.3333e-021 | C. родинка/секунда | ||
| 5.0183e+003 | D. молекула/секунда | ||
| параметр | K4 | 0.005 | A. гм |
| 5e-9 | B. родинка/литр | ||
| 5e-21 | C. родинка | ||
| 3011 | D. молекула | ||
| разновидности | Xplus (неактивный) | 0.99 | A. гм |
| 9.9e-7 | B. родинка/литр | ||
| 9.9e-19 | C. родинка | ||
| 5.962e+5 | D. молекула | ||
| разновидности | X (активный) | 0.01 | A. гм |
| 1e-8 | B. родинка/литр | ||
| 1.0e-20 | C. родинка | ||
| 6.022e+3 | D. молекула |
Это - симуляция минимального митотического генератора Голдбетера с уровнем и алгебраическими уравнениями. Симулируйте с sundials решатель и разновидности C графикаM, и X. Для описания модели см. Модель SimBiology с Реакциями.
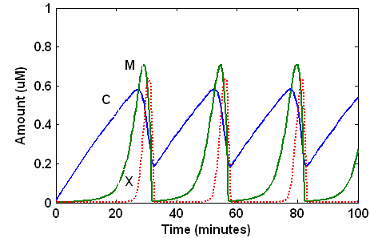
[1] Голдбетер А. (1991), “Минимальная каскадная модель для митотического генератора включающий циклин и cdc2 киназа”, Продолжения Национальной академии наук США, 88:9107-9111.
[2] Голдбетер А., Кошлэнд Д. (1981), “Усиленная чувствительность, являющаяся результатом ковалентной модификации в биологических системах”, Продолжения Национальной академии наук США, 78:6840-6844.
[3] Голдбетер А., Кошлэнд Д. (1984), “Ультрачувствительность в биохимических системах, которыми управляет ковалентная модификация”, Журнал Биологической Химии, 259:14441-14447.
[4] Голдбетер А., домашняя страница в сети, http://www.ulb.ac.be/sciences/utc/GOLDBETER/agoldbet.html.
[5] Мюррей А.В., Kirschner M.W. (1989), “Синтез циклина управляет ранним эмбриональным клеточным циклом”, Природа, 339:275-280.